Операции над векторами - АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

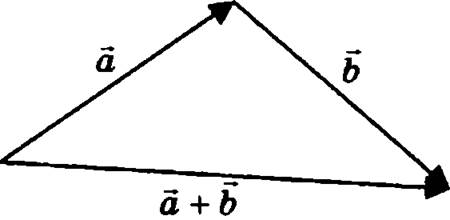
Суммой двух векторов и называется вектор начало которого совмещено с началом вектора , а конец — с концом вектора , если конец вектора совмещен с началом вектора .

При сложении векторов их соответствующие координаты складываются. Если имеем два вектора и то вектор будет иметь координаты

Свойства операции сложения векторов:

1.

2.

3. Существует вектор (нуль вектор), который, будучи прибавленным к любому другому вектору, не меняет его

4. Для каждого вектора существует вектор называемый противоположным, такой, что

Произведением вектора на число k называется вектор длина которого в |k| раз больше длины вектора , а направление совпадает с направлением вектора , если k > 0 и противоположно направлению вектора в противном случае.

При умножении вектора на число k каждая его координата умножается на k

Свойство операции умножения вектора на число:

1. k и n — числа.

2.

3. k и n — числа.

4.

Скалярным произведением вектора на вектор называется число равное произведению модулей этих векторов на косинус угла φ между ними.

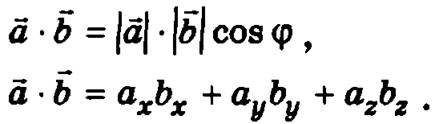
Свойства скалярного произведения векторов:

1.

2. k — некоторое число.

3.

4. причем только если

Модуль вектора и его свойства

Модуль вектора

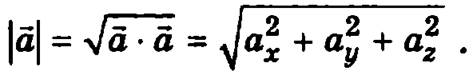
1. причем только если

2.

3.

4.

Угол φ между векторами и определяется по формуле

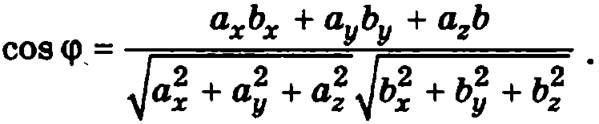
Два вектора будут ортогональны, если их скалярное произведение равно нулю.