Правила вычисления производной - ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

1. Производная алгебраической суммы функций, имеющих производную, равна такой же сумме производных этих функций

Пример.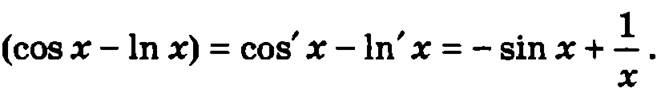

2. Производная произведения двух функций, имеющих производную, вычисляется по формуле

Пример.

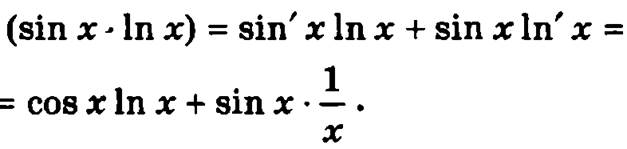
3. Производная отношения двух функций, имеющих производную, вычисляется по формуле

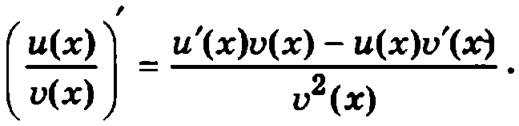
Пример.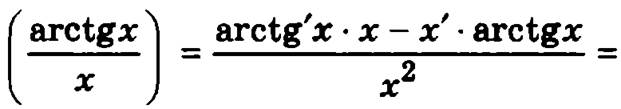

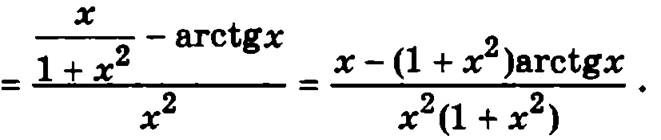
4. Если функция u = φ(х) имеет производную в точке x0, а функция у = f(u) имеет производную в точке u0, причем u0 = φ(х0), сложная функция у = f(φ(х)) будет иметь производную в точке х0 и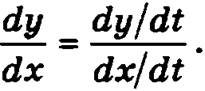

Пример. Вычислим производную сложной функции у = есоsх. В данном случае у = у(u)еu, а u = φ(х) = cos х. Тогд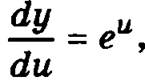а а 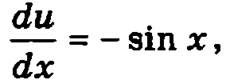следовательно

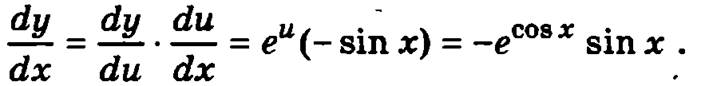
5. Производная функции, заданной параметрически, то есть в виде соотношения 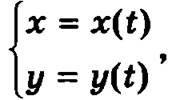где t изменяется в пределах некоторого множества, определяется по формуле

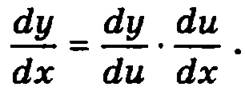
Пример. Найдем производную следующей функции, заданной параметрически

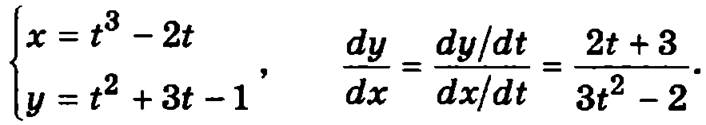
Таким образом производная параметрически заданной функции будет тоже функция, заданная параметрически