Путешествие в историю математики - Свечников А. А. 1995
Из истории арифметических действий
Сложение
Еще в древности люди научились считать предметы, называя число их по порядку: 1, 2, 3... Но сущность счета не только в том, чтобы называть по порядку числа, но и в присчитывании, т. е. в прибавлении единицы к первоначальному числу, затем еще одной единицы, затем еще одной и т. д. Овладение счетом требует умения прибавлять единицу к любому числу и к полученному от этого сложения числу снова прибавлять единицу и т. д.
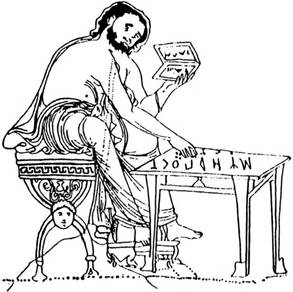
Итак, сложение числа с единицей возникло с появлением счета. В дальнейшем сложение двух чисел выразилось в присчитывании к данному числу по одному всех единиц второго слагаемого. Понаблюдайте, как складывают числа малыши. Например, чтобы прибавить к трем два, ребенок на одной руке оставляет незагнутыми 3 пальца, а на второй — 2 пальца и сначала считает три пальца (загибая каждый) на одной руке, а затем также присчитывает к ним по одному пальцы другой руки. Когда все пальцы загнуты — сложение закончено. На следующем этапе обучения ребенок уже не пересчитывает единицы первого слагаемого, а сразу называет его и присчитывает к нему по одному все единицы второго слагаемого.
Сотни лет люди древнего мира выполняли сложение подобным же образом, присчитывая к первому данному множеству предметов по одному предмету, взятому из второго множества, до тех пор, пока все предметы (члены) второго множества не будут исчерпаны.
Длительное время сложение чисел люди выполняли только устно с помощью каких-либо предметов — пальцев, камешков, ракушек, бобов и пр., а позже на специальных приборах — счетной скамье, абаке, счетах.
Только после того как была изобретена позиционная система счисления и числа стали записывать цифрами, подобно тому как это делаем мы, индийские мудрецы нашли способ сложения чисел в письменном виде. При вычислениях они записывали числа палочкой на песке, насыпанном на специально приготовленную доску. Цифры, изображенные на песке, легко было стирать, а на их месте записывать другие. Вероятно, этим можно объяснить некоторые особенности индийского приема сложения чисел.
В Древней Индии было принято записывать слагаемые в столбик — одно под другим; сумму же записывали над слагаемыми, сложение начинали с наивысшего разряда, т. е. слева направо. Если записанная в сумме цифра при сложении последующего низшего разряда изменялась, то ранее записанную цифру стирали, а на ее место вписывали новую.
Примеры:

Примечание. Здесь знак х указывает, что в числе 13 сначала была записана цифра 1, а затем она прибавлена к сумме 3 + 6 = 9 и вписано не 9, а 10.
Индийский прием сложения позаимствовали математики Среднего и Ближнего Востока, а от них в начале IX в. он перекочевал в Европу.
С XV в. способ письменного сложения чисел принял современный вид, а до этого долгое время слагаемые записывали одно подле другого без всякого знака между ними. В начале XV в. действие сложения стали обозначать начальной буквой слова плюс (в латинском алфавите — Р), которое означало «сложить». К концу того же века отдельные математики стали обозначать сложение знаком 4-, который вскоре получил всеобщее признание. Это быстрое признание нового знака произошло, видимо, потому, что его начертание напоминает сложение двух палочек.
В Древнем Египте знаком сложения служило схематическое изображение шагающих ног человека.
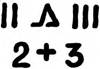
Однако изобретение особых знаков для обозначения арифметических действий нельзя полностью приписывать только европейским математикам. Еще древние египтяне обозначали сложение особым знаком — рисунком шагающих ног.
Название слагаемое впервые встречается в работах математиков XIII в., а понятие «сумма» получило современное толкование только в XV в. До этого времени оно имело более широкий смысл — суммой называли результат любого из четырех арифметических действий.
Вычитание
В Древней Индии вычитание чисел выполняли способом отсчитывания от уменьшаемого по одному, пока не получится вычитаемое. Например, вычитая от девяти пять, считали: «Девять без одного — восемь, девять без двух — семь, девять без трех — шесть, девять без четырех — пять, девять без пяти — четыре. Все единицы вычитаемого (пять) исчерпаны, следовательно, 9 - 5 = 4».
Второй способ вычитания (австрийский) состоит в прибавлении к вычитаемому такого числа, которое в сумме с вычитаемым даст уменьшаемое. При таком способе, например, считали: «9 - 5: пять прибавить один — шесть, пять прибавить два — семь, пять прибавить три — восемь, пять прибавить четыре — девять. Следовательно, 9 - 5 = 4, так как, прибавив к пяти четыре, получаем уменьшаемое — девять».
Индийские математики выполняли вычитание больших чисел способом, похожим на сложение. Они начинали вычитание с наивысших разрядов, причем те цифры, от которых приходилось «занимать» единицу, чтобы раздробить ее в десяток низших разрядных единиц, они стирали и записывали на место стертой новую, на единицу меньшую цифру. Для них это было удобно, так как в Индии черновые вычисления выполняли на доске, посыпанной песком.
Индийский способ вычитания переняли арабы. Но они не стирали цифры, а перечеркивали их и надписывали новую цифру над перечеркнутой. Это было очень неудобно. Тогда арабские математики, используя тот же прием вычитания, стали начинать действие с низших разрядов, т. е. разработали новый способ вычитания, сходный с современным.
Для обозначения вычитания в III в. до н. э. в Греции использовали перевернутую греческую букву пси (Ψ). Итальянские математики пользовались для обозначения вычитания буквой М (m), начальной в слове минус. В XVI в. для обозначения вычитания стали применять знак —. Вероятно, этот знак перешел в математику из торговли. Торговцы, отливая для продажи вино из бочек, черточкой мелом обозначали число мер проданного из бочки вина. Чтобы отличать знак минус от тире, Л. Ф. Магницкий (XVIII в.) обозначал вычитание знаком ÷.
Знак равенства (=) впервые введен английским учителем математики Р. Рикоррдом в XVI в. Он пояснял: «Никакие два предмета не могут в большей степени быть равны между собой, как две параллельные линии». Но еще в египетских папирусах встречается знак, который обозначал равенство двух чисел, хотя этот знак совершенно не похож на знак =.
Названия уменьшаемое и вычитаемое появились в Европе только в XVIII в. А слово разность введено на 250 лет раньше.
Умножение
Умножение — это особый (частный) случай сложения нескольких одинаковых чисел. В далекие времена люди учились умножать уже при счете предметов. Так, считая по порядку числа 17, 18, 19, 20, они должны были представлять 20 не только как 10 + 10, но и как два десятка, т. е. 2 • 10, 30 — как три десятка, т. е. три раза повторить слагаемым десяток — 3 • 10 — и т. д.
Умножать люди начали значительно позже, чем складывать. Египтяне выполняли умножение посредством повторного сложения или последовательного удвоения. Например, чтобы умножить 27 на 13, они составляли запись, подобную следующей:
*1 — 27 (складывая 27 + 27 или удваивая 27 • 2, они получали 2 — 54; сложение или удвоение повторяли):
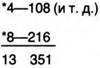
Из первого столбика вычислитель выбирал те числа, которые в сумме составляли множитель (13), т. е. 1 + 4 + 8, и отмечал их условными значками (у нас эти числа отмечены звездочкой *). Затем удвоенные числа, стоящие против отмеченных звездочкой, складывали и получали произведение. Этот прием (им пользовались во многих местах, в том числе и в нашей стране) применялся на практике продолжительное время. Ему даже дали название «способ умножения, применяемый русскими крестьянами».
В Вавилоне при умножении чисел пользовались специальными таблицами умножения — «предками» современных.
В Древней Индии применяли способ умножения чисел, тоже довольно близкий к современному. Индийцы производили умножение чисел начиная с высших разрядов. При этом они стирали те цифры, которые при последующих действиях надо было заменять, так как к ним прибавляли число, ныне запоминаемое нами при умножении.
Таким образом, математики Индии сразу записывали произведение, выполняя промежуточные вычисления на песке или в уме.
Индийский прием умножения, напомню, перешел к арабам. Но арабы не стирали цифры, а перечеркивали их и надписывали новую цифру над перечеркнутой.
В Европу индийский способ умножения пришел через арабов. Только в XV в. европейские математики отказались от перечеркивания неточных цифр и стали начинать умножение с низших разрядов. Европейскими математиками было разработано около десятка различных вариантов приема умножения, например умножение «решеткой» и др.
В Европе продолжительное время произведение называли сумма умножения. Название множитель упоминается в работах VI в., а множимое — в XIII в.
В России впервые дал названия всем членам (компонентам) умножения в начале XVIII в. Л. Ф. Магницкий — автор учебника «Арифметика». В нем он указал:

Для обозначения действия умножения одни из европейских математиков XVI в. употребляли букву М, которая была начальной в латинском слове, обозначавшем увеличение, умножение, — мультипликация (от этого слова произошло название «мультфильм»). В XVII в. некоторые из математиков стали обозначать умножение косым крестиком — х, а иные употребляли для этого точку. В XVI — XVII вв. для обозначения действий применяли различные символы — единообразия в их употреблении не было. Только в конце XVIII в. большинство математиков стали употреблять в качестве знака умножения точку, но допускали и употребление косого креста. Знаки умножения (•, х) и знак равенства (=) стали общепризнанными благодаря авторитету знаменитого немецкого математика Готфрида Вильгельма Лейбница (1646 — 1716).
Деление
Два любых натуральных числа всегда можно сложить, а также умножить. Вычитание из натурального числа можно выполнить лишь тогда, когда вычитаемое меньше уменьшаемого. Деление же без остатка выполнимо только для некоторых чисел, причем узнать, делится ли одно число на другое, трудно. Помимо того, есть числа, которые вообще нельзя разделить ни на какое число, кроме единицы. Делить на нуль нельзя. Эти особенности действия значительно усложнили путь к уяснению приемов деления.
В Древнем Египте деление чисел выполняли способом удвоения и медиации, т. е. делением на два с последующим сложением отобранных чисел. Например, чтобы разделить 60 на 12, египетские математики поступали так: 60 : 12
1 —12*
2 — 24
4 — 48*
8 — 96
(т. е. составляли табличку, в которой делитель (12) сначала удваивали, затем учетверяли и т. д.). Из второго столбика отбирали числа, которые в сумме составляли делимое. Строки с этими числами — первую и третью (1 — 12 и 4 — 48, так как 12 + 48 = 60) отмечали особым значком (здесь они отмечены звездочкой). Отмеченные числа складывали и получали ответ: 1 + 4 = 5, так как 12 + 48 = 60. Следовательно, 60 :12 = 5.
А вот более сложный пример: 492 : 12
1 — 12*
2 — 24
4 — 48
8 — 96*
16 — 192
32 — 384*
Поступаем так же, как в первом случае: так как 492 = 384 + 96 + 12, то 492 :12 = (32 + 8 + 1). Следовательно, 492 : 12 = 41.
Математики Индии изобрели способ «деление вверх». Они записывали делитель под делимым, а все промежуточные вычисления — вверху над делимым. Причем те цифры, которые при промежуточных вычислениях подвергались изменению, индийцы стирали и на их место писали новые.
Позаимствовав этот способ, арабы в промежуточных вычислениях стали цифры перечеркивать и надписывать над ними другие. Такое нововведение значительно усложнило «деление вверх». Запись деления получалась очень громоздкой и для многих непонятной (поэтому мы его здесь не приводим). Даже знающие люди допускали при таком способе деления ошибки. Однако европейские математики восприняли способ деления от арабов и пользовались им до XVIII в. Вот почему среди итальянских поговорок сохранилась: «Трудная вещь — деление», а человек, усвоивший в то время деление, получал звание «доктора абака».
Способ деления, близкий к современному, впервые появился в итальянской рукописи 1460 г. Этот способ отличался от современного лишь тем, что остаток при вычитании частичного произведения делителя на отдельные разряды частного записывался дважды. Вот, например, как делили числа в XV — XVII вв.

Примечание: подчеркнутые цифры записывали в частное, словесные пояснения и вычисления в скобках приведены для ясности; все приведенные вычисления выполняли в уме.
Потребовалось около трех веков, чтобы указанный способ деления был окончательно усовершенствован и в современном виде принят всеми математиками мира. Попыток усовершенствовать деление было сделано немало, и поэтому приемов деления существовало около десятка.
На протяжении тысячелетий действие деления не обозначали каким-либо знаком — его просто называли и записывали словом. Индийские математики первыми стали обозначать деление начальной буквой из названия этого действия. Арабы ввели для обозначения деления черту. Черту для обозначения деления от арабов перенял в XIII в. итальянский математик Фибоначчи. Он же впервые употребил термин частное.
Фибоначчи.

Знак двоеточия (:) для обозначения деления вошел в употребление в конце XVII в. До этого у некоторых математиков встречался знак ÷, которым они обозначали это действие.
Результат деления в продолжение нескольких столетий называли сумма. В России названия делимое, делитель, частное впервые ввел Л. Ф. Магницкий в начале XVIII в. Он в своей книге «Арифметика» привел два способа деления — «деление вверх» и второй способ, близкий к современному.