Математика 5 класс - Поурочные разработки
Простые и составные числа - Простые и составные числа - Делимость чисел
Цели: ввести новые понятия, связанные с делимостью чисел, формировать умение распознавать простые и составные числа.
Ход урока
I . Организационный момент.
II. Устная работа.
Заполните прямоугольники в схеме (рис. 120).
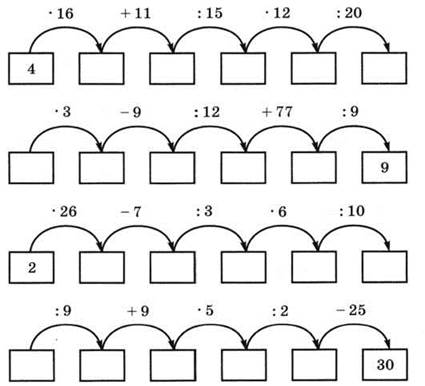
Рис. 120
III. Актуализация знаний.
Даны числа 24, 5, 18, 28, 37, 55, 75, 25, 53, 72, 11.
1. Нарисуйте в тетради данную таблицу и заполните ее.
Число |
Делители |
Количество делителей |
24 |
||
5 |
||
18 |
||
28 |
||
37 |
||
55 |
||
75 |
||
25 |
||
53 |
||
72 |
||
11 |
2. На какие две группы по количеству можно разделить эти числа?
3. Дополните каждую группу несколькими числами.
IV. Изучение нового материала.
1. Работа с текстом учебника.
1). Сформулировать определения простых и составных чисел. Обратить внимание учащихся на то, что 1 — ни простое, ни составное число.
2). У, № 542, 543 (устно).
2. 1). Исторический экскурс в мир простых чисел.
Рассмотреть решето Эратосфена и воспользоваться им для поиска простых чисел в пределах сотни. Знакомство с таблицей простых чисел.
2). У, № 549, 550 (устно).
3. Разложение составного числа на простые множители.
1). Рассмотрите записи 24 = 2 · 12; 24 = 2 · 2 · 6; 24 = 2 · 2 · 2 · 3. Что вы можете о них сказать? Какие преобразования выполнены с числом 24?
2). Рассмотрите графы (рис. 121). Объясните, как они построены. Существует ли между ними и равенствами из п. 1 связь? Если существует, то какая?
Эти графы называются деревьями. В начальной вершине этого дерева записано натуральное число.
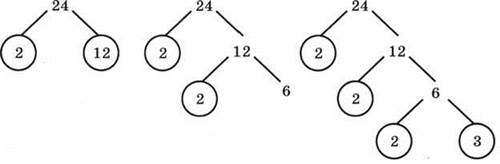
Рис. 121
3). Какое преобразование совершается с этим числом?
4). Постройте деревья для чисел 48, 100. Обратите внимание на обведенные числа.
Когда мы строим для числа дерево, то совершаем с числом важную математическую операцию, которая называется разложением числа на простые множители.
![]()
5). Разложите число 204 на простые множители, построив дерево этого числа (рис. 122).
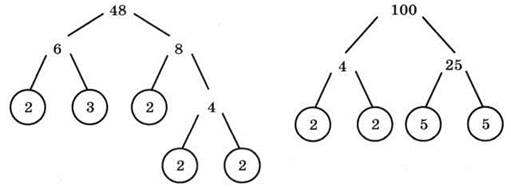
Рис. 122
6). На вершинах дерева записаны такие числа: {2, 3, 3, 3, 3}, {2, 3, 7}, {2, 2, 5, 7}. Для каких чисел строились деревья?
4. Основная теорема арифметики.
Каждое натуральное число, за исключением 1, раскладывается в произведение простых сомножителей, причем единственным образом.
Простые числа являются кирпичиками, из которых можно построить все остальные числа. Рассмотрим число 420. Оно составное. Его можно разложить на множители так:
![]()
V. Формирование умений и навыков.
1. У, № 544 (а).
2. Какое число разложено на простые множители: 22 · 3 · 5, 2 · 32 · 7, 22 · 32 · 5?
VI. Итоги урока.
1. Какое натуральное число называется простым? составным?
2. Какое натуральное число не является ни простым, ни составным? Ответ объясните.
VII. Домашнее задание.
У, п. 6.2, № 544 (б), 545, 547, 548.