Прямая и обратная пропорциональная зависимости - урок 3 - ОТНОШЕНИЯ И ПРОПОРЦИИ - ОБЫКНОВЕННЫЕ ДРОБИ

Цели: отрабатывать умение решать задачи с помощью пропорции, уравнения, записанные в виде пропорции; подготовить учащихся к контрольной работе по теме «Отношения и пропорции»; проверить знания и умения учащихся по изученному материалу.

Ход урока

I. Организационный момент

II. Устный счет

1. Пешеход затратил на путь 2 ч, двигаясь со скоростью 6 км/ч. Сколько времени затратит он на тот же путь, если его скорость будет 4 км/ч?

2. Найдите значение выражений:

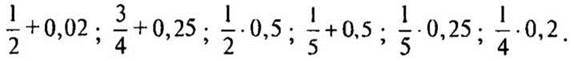
3. Из пункта А в пункт В автомобиль ехал 1 ч 20 мин, обратный путь он ехал с той же скоростью, но 80 мин. Почему?

4. Что идет, не двигаясь с места? (Время.)

5. Все натуральные числа до 100 записаны в один ряд. Сколько раз повторяется цифра 0 в этом ряду? (11 раз.)

III. Индивидуальная работа

1 карточка

Решите задачи, составив пропорции.

1. Скорость голубя 90 км/ч, ласточки — 150 км/ч. Какую часть пути ласточки пролетит голубь за то же время полета?

2. Три ученика пропололи грядку за 4 ч. За сколько часов выполнят работу два ученика?

2 карточка

Решите задачи, составив пропорции.

1. Сцеплены две шестерни, одна из них имеет 24 зубца, вторая имеет 8 зубцов. Вторая шестерня сделала два полных оборота. Какую часть полного оборота сделала за это время первая шестерня?

2. Четыре гнома посадили для Белоснежки 8 кустов роз. Сколько кустов роз за то же время посадят три гнома?

IV. Сообщение темы урока

— Сегодня на уроке мы продолжим отрабатывать свои умения решать пропорции и задачи с помощью пропорций.

V. Физкультминутка

VI. Закрепление изученного материала

1. № 788 стр. 130 (после разбора самостоятельно).

Прочитайте задачу.

— Что неизвестно? (Сколько посадили лип.)

— Сколько процентов лип посадили? (100%.)

— Сколько процентов лип принялось? (95%.)

— Сколько лип принялось? (57 лип.)

— Какая зависимость между рассматриваемыми величинами?

— Составьте краткую запись в виде таблицы.

— Самостоятельно решите задачу.

Решение:

Пусть х лип — посадили.

Посадили	х л.	100%
Принялось	57 л.	95%

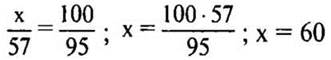
(Ответ: 60 лип посадили.)

2. № 793 стр. 131 (самостоятельно, самопроверка).

Решение:

Пусть х кг — примесей.

	Количество частей	Масса
Железо Примеси	7 ч. 3 ч.	73,5 кг x

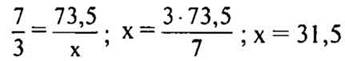
31,5 кг - примесей.

(Ответ: 31,5 кг.)

VII. Повторение изученного материала

1. № 796 стр. 131 (у доски и в тетрадях).

— Если знаменатель 6, то какие знаменатели будут у дробей, которые являются слагаемыми? (2 и 3.)

— Проверим: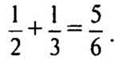

Решение:

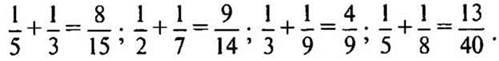
2. № 763 (з, и) стр. 125.

— Что такое пропорция?

— Как называются числа в пропорции?

— Как найти неизвестные члены пропорции?

— Как проверить, верно ли вы решили уравнение?

— На каком свойстве пропорции основана проверка?

Решение:

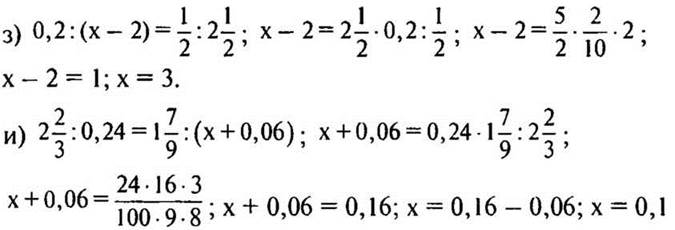
(Ответ: з) х = 3; и) х = 0,1.)

VIII. Самостоятельная работа (10—15 мин)

Вариант I

1. Решите уравнение: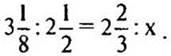

Решите задачи, составив пропорции.

2. На 20 км пути автомашина расходует л горючего. Сколько горючего автомашина израсходует на 50 км пути?

3. Для отопления здания заготовлено угля на 180 дней при норме расхода 0,6 т угля в день. На сколько дней хватит этого запаса, если его расходовать ежедневно по 0,5 т?

4. Напишите все двузначные числа, для записи которых употребляются только цифры 0, 1, 3, 5, и подчеркните те из них, которые кратны 3.

Вариант II

1. Решите уравнение: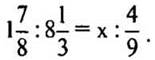

Решите задачи, составив пропорции.

2. На изготовление 8 деталей требуется г серебра. Сколько серебра потребуется на изготовление 12 таких деталей?

3. 24 человека за 6 дней пропололи участок клубники. За сколько дней выполнят ту же работу 36 человек, если будут работать с такой же производительностью?

4. Напишите все двузначные числа, для записи которых употребляются только цифры 0, 4, 6, 6, и подчеркните те из них, которые кратны 3.

IX. Подведение итогов урока

— Приведите примеры величин, у которых зависимость не является ни прямо, ни обратно пропорциональной.

— Почему зависимость между количеством товара и стоимостью покупки прямо пропорциональна? (Если купить товара в несколько раз больше, то и стоимость покупки увеличится во столько же раз.)

— Почему зависимость между шириной и длиной при одном и том же значении площади прямоугольника обратно пропорциональна? (Если увеличить длину прямоугольника в несколько раз, то надо ширину во столько же раз уменьшить.)

Домашнее задание

№ 812, 817, 818 стр. 133.