Величины, характеризующие колебательное движение - МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ. ЗВУК - Поурочные разработки по программе А. В. Перышкина

Цели урока:

Ввести понятия амплитуды, периода и частоты колебаний; сформировать представление о гармонических колебаниях.

Ход урока

I. Проверка домашнего задания, повторение

- Приведите примеры колебательных движений.

- Как вы понимаете утверждение о том, что колебательное движение периодично?

- Что такое период колебаний?

- Какие колебания называются свободными?

- Что такое смещение, амплитуда?

- Что такое колебательные системы?

- Что называется маятником?

- Какие тела входят в колебательную систему, называемую пружинным маятником? Нитяным (математическим) маятником?

II. Новый материал

Каждое движение характеризуется своими величинами.

- Какими величинами характеризуется равномерное прямолинейное движение? (Постоянной скоростью, координатой. Существует уравнение зависимости координаты от времени х = х₀ +v_xt.)

- Какими величинами характеризуется прямолинейное движение? (Постоянным ускорением, координатой.)

- Какими же величинами характеризуется колебательное движение?

Период колебаний

На прошлом уроке уже отмечалось, что колебательное движение - периодическое. Период Т - время одного полного колебания:

где t - все время движения, N — количество колебаний.

В СИ период колебаний выражается в секундах: [Т] = с.

Частота колебаний

Частота v - число полных колебаний за единицу времени:

где N — количество колебаний, t - время движения.

В СИ частота выражается в герцах: [v] = с^-1 = Гц.

Колебательное движение характеризуются также циклической частотой:

Амплитуда колебания

Амплитуда х (или А) - наибольшее смещение от положения равновесия, измеряется в метрах (м). Можно измерять в единицах плоского угла (для математического маятника).

Графическое представление колебательного движения Так как в процессе колебаний положение тела меняется, то очень удобно изменение смещения тела от положения равновесия во времени представлять графически. Подготовив установку, предложенную в учебнике на стр. 97, учитель демонстрирует вид траектории движения тела. График зависимости смещения х от времени изображен на рис. 47. График показывает, что на каждом периоде колебаний Т амплитуда колебаний убывает. Это связано с наличием трения в системе. Если трение очень мало, то амплитуда убывает очень медленно, и колебания долго не затухают.

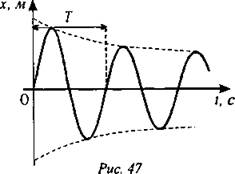
Полученная кривая называется синусоидой. (Несмотря на то, что такой термин используется в литературе, кривая, изображенная на рис. 47, не является истинной синусоидой - это более сложная функция. К сожалению, в 9 классе у ребят нет достаточных математических знаний, чтобы описать эту функцию. Истинная же синусоида показана на рис. 48.)

Периодические изменения во времени физической величины происходящие по закону синуса или косинуса, называются гармоническими колебаниями.

Закон изменения смещения х от времени t имеет вид:

Следует обратить внимание учеников, что по графику очень удобно определять все характеристики колебательного движения, а именно, период (T), амплитуду (А) и частоту (v).

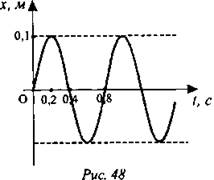
Например, по графику колебаний, изображенному на рис. 48, определяем:

А = 0,1 м,

T = 0,8 с,

v = 1 /T = 1,25 Гц.

Для данного графика: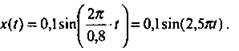

Далее можно предложить учащимся самостоятельно определить по заданному графику параметры движения тела.

Параметры колебательных систем

Чему же равны период и частота колебаний математического маятника, пружинного маятника?

а) Для пружинного маятника:

где m - масса груза, k - жесткость пружины.

Тогда частота колебаний:

б) Для математического маятника:

где l - длина нити, g - ускорение свободного падения

Частота колебаний:

Необходимо отметить отличие гармонических колебаний от негармонических. Период гармонических колебаний не зависит от способа выведения системы из положения равновесия (например, от амплитуды колебаний). В этом можно будет легко убедиться на следующем уроке в ходе лабораторной работы.

III. Упражнения и вопросы для повторения

- Какие колебания называются гармоническими?

- Что называют частотой колебаний? Какова единица измерений?

- Что называют амплитудой колебаний?

- Что называют периодом колебаний? Какая формула выражает смысл этого понятия? Какова единица измерения периода колебаний?

- Какое уравнение выражает смысл гармонического колебания?

- Как найти период математического маятника? Пружинного маятника?

IV. Решение задач

Задача 1

Маятник совершил 20 колебаний за 1 мин. 20 с. Найти период и частоту колебаний. (Ответ: T = 4 с; v = 0,25 Гц.)

Задача 2

Амплитуда незатухающих колебаний точки струны 2 мм, частота колебаний 1 кГц. Какой путь пройдет точка струны за 0,4 с? Какое перемещение совершит эта точка за один период колебаний? (Ответ: l = 3,2 м; S = 0.)

Задача 3

Координата колеблющегося тела изменяется по закону: х = 5cosπt. Чему равны амплитуда, период и частота колебаний, если в формуле все величины выражены в единицах СИ? (Ответ: А = 5 м; Т = 2 с; v = 0,5 Гц.)

Задача 4

Математический маятник длиной 2,45 м совершил 100 колебаний за 314 с. Определить ускорение свободного падения для данной местности. (Ответ: g = 9,8 м/с².)

Задача 5

Какова длина математического маятника, совершающего гармонические колебания с частотой 0,5 Гц на поверхности Луны? Ускорение свободного падения на поверхности Луны 1,6 м/с². (Ответ: l = 0,16 м.)

Задача 6

Груз массой 0,4 кг, подвешенный к невесомой пружине, совершает 30 колебаний в минуту. Чему равна жесткость пружины? (Ответ: k = 4 Н/м.)

Домашнее задание

1. Выучить § 26, 27;

2. Задачи на усмотрение учителя (3 из предложенных).