Решение задач на совместное движение нескольких тел. Ускорение - ЗАКОНЫ ВЗАИМОДЕЙСТВИЯ И ДВИЖЕНИЯ ТЕЛ - Поурочные разработки по программе А. В. Перышкина

Цели урока:

Научить учащихся решать задачи на совместное движение нескольких тел. Проверить их навыки и умения решать задачи. Сформировать понятие ускорения.

Ход урока

I. Повторение. Проверка домашнего задания

- Какое движение называют равномерным?

- Что называется скоростью равномерного движения? В каких единицах она выражается?

- В каких случаях проекция скорости равномерного движения на ось положительна, в каких отрицательна?

- Как находится проекция перемещения, если известна проекция скорости?

- Как найти координату тела в любой момент времени, если известна начальная координата, проекция скорости и время?

- Как скорость, выраженную в метрах в секунду, выразить в километрах в час и наоборот?

- Выразите в м/с скорость 72 км/ч.

- Какая скорость больше: 5 м/с или 36 км/ч?

II. Решение задач

Задача 1

В течение 30 с поезд двигался равномерно со скоростью 54 км/ч. Какой путь прошел поезд за это время? (Ответ: 450 м.)

Задача 2

Движения двух велосипедистов заданы уравнениями х₁ = 5t и х₂ = 150 – 10t.

а) Постройте графики зависимости х(t);

б) Найдите время и место встречи;

в) Постройте графики зависимости v_x(t).

(Ответ: тела встретятся через t = 10 с, х = 50 м.)

Задание 3

Точка А совершает движение на плоскости XY. Координаты точки, в зависимости от времени изменяются по закону: х = -2t, y = 2 + 3t.

а) Запишите уравнение траектории y(x) точки А.

б) Чему равны начальные координаты движущейся точки и координаты через 2 с после начала движения?

в) Постройте график функции y(х).

(Ответ: в начальный момент t = 0; х = 0. Через 2 с х = -4 м; у = 8 м.)

III. Самостоятельная работа

I вариант

На оси координат показаны тела, их скорости (рис. 14).

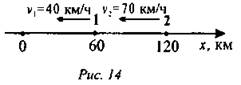
а) Определить начальные координаты первого и второго тела.

б) Записать для каждого тела уравнение зависимости координаты от времени - х(t).

в) Найти место и время встречи аналитически и графически.

г) Построить график v_x(t).

д) Найти координату каждого тела через 4 ч.

е) Найти путь, пройденный каждым телом за 6 ч.

II вариант

На оси координат показаны тела, их скорости (рис. 15).

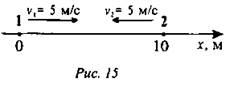
а) Определите начальные координаты 1 и 2 тела.

б) Записать для каждого тела уравнение зависимости координаты от времени.

в) Найти место и время встречи аналитически и графически.

г) Построить график v_x(t).

д) Найти координату каждого тела через 4 с.

е) Найти путь, пройденный каждым телом за 6 секунд.

IV. Новый материал

Прямолинейное равномерное движение, т. е. движение с постоянной (по модулю и направлению) скоростью, не очень часто встречается на практике.

Гораздо чаще приходится иметь дело с таким движением, при котором скорость со временем изменяется. Такое движение называется неравномерным.

Эксперимент

Рассмотрим движение шарика по наклонному желобу, а затем по горизонтальному участку (рис. 16).

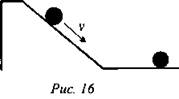
Координаты шарика через 2 с представлены в таблице:

t. с	0	2	4	6	8
x, см	0	8	32	72	128

Видно, что перемещения шарика за 2 с различны на разных этапах движения. При таком движении скорость тела (мгновенная скорость) непрерывно изменяется от точки к точке.

Для простоты будем считать, что за каждую единицу времени и вообще за любые равные промежутки времени скорость изменяется одинаково.

Движение тела, при котором его скорость за любые равные промежутки времени изменяется одинаково, называется равноускоренным движением.

Пусть скорость тела в начальный момент времени была равна , а через промежуток времени t она оказалась равной . Тогда отношение - быстрота изменения скорости. Ее называют ускорением:

Единица измерения ускорения в СИ - м/с²: [a] = м/с².

При прямолинейном движении векторы и направлены вдоль одной прямой. Удобнее использовать запись: В проекциях на ось ОХ это уравнение имеет вид:

Алгоритм решения простейших задач по кинематике:

1. Выясните и запишите характер движения.

2. Выясните и запишите, есть ли начальная скорость.

3. Запишите краткое условие задачи, выразив все величины в единицах СИ.

4. Используя основные формулы кинематики, запишите ее в векторной форме, спроецируйте на необходимую ось.

5. Запишите проекции с учетом знаков (в модулях).

6. Найдите искомую величину.

7. Вычислите ее.

8. Проанализируйте ответ.

Пример 1

Автомобиль, движущийся со скоростью 10 м/с, начал тормозить с ускорением 1 м/с². Сколько времени пройдет до остановки автомобиля?

Дано:

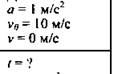
Решение:

Запишем уравнение для скорости при равноускоренном движении в проекциях на ось ОХ:

Т. к. векторы скорости и ускорения направлены в противоположные стороны, то их проекции имеют разные знаки. Получаем уравнение: v = v₀ - at.

Отсюда:

Ответ: t = 10 с.

Пример 2

Тело движется прямолинейно с уменьшающейся скоростью. Ускорение равно 4 м/с². В некоторый момент времени модуль скорости тела v₀ = 20 м/с. Найдите скорость тела через t₁ = 4 c и t₂, = 8 c после этого момента. Определите также момент времени, когда тело останавливается.

Дано:

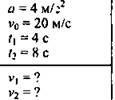
Решение:

Т. к. векторы скорости и ускорения направлены в противоположные стороны, то в проекциях на ось ОХ получаем уравнения: v_1x = v₀ – at₁, v_2x = v₀ - at₂.

Знак минус у проекции скорости означает, что к исходу 8-ой секунды тело двигалось в направлении, противоположном направлению начальной скорости. Модуль скорости v₂ = ? v_2X? = 12 м/с.

Можно вычислить момент, когда тело остановилось, т. е. когда v₃ = 0:

Ответ: v₁ = 4 м/с; v₂ = -12 м/с, t = 5 с (время остановки тела).

V. Решение задач

Для самостоятельного решения в классе учащимся можно дать следующие задачи:

Задача 1

Троллейбус, трогаясь с места, движется с постоянным ускорением 1,5 м/с². Через какое время он приобретет скорость 54 км/ч? (Ответ: через 10 с.)

Задача 2

Автомобиль, движущийся со скоростью 36 км/ч, останавливается при торможении в течение 4 с. С каким постоянным ускорением движется автомобиль при торможении? (Ответ: 2,5 м/с².)

Задача 3

Автомобиль, двигаясь с постоянным ускорением, на некотором участке увеличил свою скорость с 15 м/с до 25 м/с. За какое время произошло это увеличение, если ускорение автомобиля равно 1,6 м/с²? (Ответ: 6,25 с.)

Задача 4

Какая скорость могла быть достигнута, если бы тело в течение 0,5 ч двигалось с ускорением 10 м/с² из состояния покоя? (Ответ: 18000 м/с.)

Домашнее задание

1. Выучить § 5;

2. Упр. 5 (учебник, стр. 24);

3. Задача 7 (учебник, стр. 241).