Информатика - Методическое пособие для 7-9 классов - 2015 год
Запись вспомогательных алгоритмов на языке Паскаль - МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ПРОВЕДЕНИЮ УРОКОВ В 9 КЛАССЕ
Планируемые образовательные результаты:
• предметные — представления о способах записи вспомогательных алгоритмов в языке Паскаль;
• метапредметные — умение самостоятельно планировать пути достижения целей; умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности, определять способы действий в рамках предложенных условий, корректировать свои действия в соответствии с изменяющейся ситуацией; умение оценивать правильность выполнения учебной задачи;
• личностные — алгоритмическое мышление, необходимое для профессиональной деятельности в современном обществе; представление о программировании как сфере возможной профессиональной деятельности.
Решаемые учебные задачи:
1) напомнить сущность понятия вспомогательного алгоритма, ввести понятие подпрограммы;
2) познакомить с правилами оформления подпрограммы в виде процедуры;
3) познакомить с правилами оформления подпрограммы в виде функции;
4) познакомить с примером рекурсивной функции.
Основные понятия, рассматриваемые на уроке:
• вспомогательный алгоритм;
• формальные параметры;
• фактические параметры;
• подпрограмма;
• процедура;
• функция;
• рекурсивная функция.
Средства ИКТ, используемые на уроке:
• персональный компьютер (ПК) учителя, мультимедийный проектор, экран;
• ПК учащихся.
Электронное приложение к учебнику:
• презентация “Запись вспомогательных алгоритмов на языке Паскаль”.
Особенности изложения содержания темы урока
Данная тема имеет повышенный уровень сложности. Ее рассмотрение может быть проведено в ознакомительном порядке или вообще отложено для дальнейшего изучения в 10-11 классах. Наиболее подготовленным ученикам можно предложить самостоятельно разобраться в готовых текстах программ.
Указания, комментарии, ответы и решения
Задания в тексте параграфа
1. Задание в конце пункта 2.4.1 (с. 91).
а) Результат работы программы НОД = 3.


б) Десять целых двузначных чисел задаются случайным образом.

2. Первое задание в пункте 2.4.2 (с. 92).


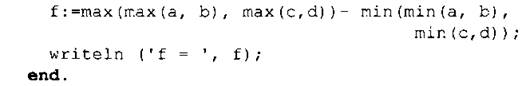
3. Второе задание в пункте 2.4.2 (с. 93). Программа, вычисляющая и выводящая на экран 10 первых членов последовательности Фибоначчи.

Задания в учебнике (после параграфа)
№ 4. Наименьшее общее кратное (НОК) двух целых чисел m и n есть наименьшее натуральное число, которое делится на m и n без остатка.
НОД(m, n) и НОК(m, n) связаны соотношением:
НОД(m, n) ∙ НОК(m, n) = m ∙ n.

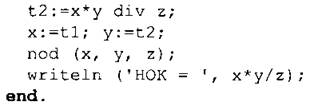
№ 5

№ 6. Возможный вариант решения задачи.


№ 7

№ 8. Здесь нет явных ограничений на х и n. В связи с этим может возникнуть потребность в типе longint.


№ 9

№ 10
