Упражнения с решениями - Урок 2 - Основы анализа алгоритмов

Упражнение с решением 1

Расположите функции из следующего списка по возрастанию скорости роста. Другими словами, если функция g(n) в вашем списке следует непосредственно после f(n), из этого следует, что f(n) = O(g(n)).

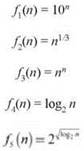
Решение

С функциями f₁, f₂ и f₄ все просто — они принадлежат базовым семействам экспоненциальных, полиномиальных и логарифмических функций. В частности, согласно (2.8), f₄(n) = O(f₂ (n)), а согласно (2.9), f₂(n) = O(f₁(n)).

Разобраться с функцией f₃ тоже не так уж сложно. Сначала она растет медленнее 10ⁿ, но после n ≥ 10 очевидно 10ⁿ ≤ nⁿ. Это именно то, что нужно для определения O(∙): для всех n ≥ 10 выполняется условие 10ⁿ ≤ cnⁿ, где в данном случае c = 1, а значит, 10ⁿ = O(nⁿ).

Остается функция f₅, которая выглядит, откровенно говоря, несколько странно. В таких случаях бывает полезно вычислить логарифм и посмотреть, не станет ли выражение более понятным. В данном случае Как выглядят логарифмы других функций? Bce эти выражения могут рассматриваться как функции log₂ n; используя обозначение z = log₂ n, получаем

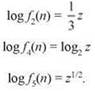
Теперь происходящее становится более понятным. Прежде всего, для z ≥ 16 имеем log₂ z ≤ z^1/2. Но условие z ≥ 16 эквивалентно n ≥ 2¹⁶ = 65 536; следовательно, после n ≥ 2¹⁶ выполняется условие log f₄(n) ≤ log f₅(n), а значит, f₄(n) ≤ f₅(n). Из этого следует, что f₄(n) = O(f₅(n)). Аналогично получаем z^1/2 ≤ 1/3z при z ≥ 9 — иначе говоря, при n ≥ 2⁹ = 512. Для n, больших этой границы, выполняется условие log f₅(n) ≤ log f₂(n); следовательно, f₅(n) ≤ f₂(n), и f₅(n) = O(f₂(n)). Фактически мы определили, что скорость роста функции лежит где-то между логарифмическими и полиномиальными функциями.

Функция f₅ занимает место в списке между f₄ и f₂, а упорядочение функций на этом завершается.

Упражнение с решением 2

Пусть f и g — две функции, получающие неотрицательные значения, и f = O(g). Покажите, что g = Ω(f).

Решение

Это упражнение помогает формализовать интуитивное ощущение, что O(∙) и Ω(∙) в некотором смысле противоположны. Собственно, доказать его несложно, для этого достаточно развернуть определения.

Известно, что для некоторых констант c и n₀ выполняется условие f(n) ≤ cg(n) для всех n ≥ n₀. Разделив обе стороны на с, можно сделать вывод, что g(n) ≥ 1/cf(n) для всех n ≥ n₀. Но именно это и необходимо, чтобы показать, что g = Ω(f): мы установили, что g(n) не меньше произведения f(n) на константу (в данном случае 1/c) для всех достаточно больших n (начиная с n₀).

Упражнения

1. В приведенном ниже списке указано время выполнения пяти алгоритмов (предполагается, что указано точное время выполнения). Насколько медленнее будет работать каждый из алгоритмов, если: (a) увеличить размер входных данных вдвое; (b) увеличить размер входных данных на 1?

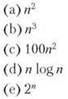
2. Есть шесть алгоритмов, время выполнения которых приведено ниже. (Предполагается, что указано точное количество выполняемых операций как функция размера данных n.) Предположим, имеется компьютер, способный выполнять 10¹⁰ операций в секунду, и результат должен быть вычислен не более чем за час. При каком наибольшем размере входных данных n результат работы каждого алгоритма может быть вычислен за час?

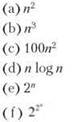
3. Расположите функции из следующего списка по возрастанию скорости роста. Другими словами, если функция g(n) в вашем списке следует непосредственно после f(n), из этого следует, что f(n) = O(g(n)).

4. Расположите функции из следующего списка по возрастанию скорости роста. Другими словами, если функция g(n) в вашем списке следует непосредственно после f(n), из этого следует, что f(n) = O(g(n)).

5. Допустим, имеются функции f и g, такие что f(n) = O(g(n)). Для каждого из следующих утверждений укажите, является оно истинным или ложным, и приведите доказательство или контрпример.

6. Рассмотрим следующую задачу: имеется массив A, состоящий из n целых чисел A[1], A[2], ..., A[n]. Требуется вывести двумерный массив B размером n х n, в котором B[i,j] (для i < j) содержит сумму элементов массива отA[i] доA[j], то есть суммуA[i] + A[i + 1] + ... + A[j]. (Для i ≥ j значение элемента массива B[i, j] остается неопределенным, поэтому выводиться для таких элементов может что угодно.)

Ниже приведен простой алгоритм решения этой задачи.

(a) Для некоторой выбранной вами функции f приведите границу времени выполнения этого алгоритма в форме O(f(n)) для входных данных размера n (то есть границу количества операций, выполняемых алгоритмом).

(b) Для той же функции f покажите, что время выполнения алгоритма для входных данных размера n также равно Ω(f(n)). (Тем самым определяется асимптотически точная граница Ө(f(n)) для времени выполнения.)

(c) Хотя алгоритм, проанализированный в частях (a) и (b), является наиболее естественным подходом к решению задачи (в конце концов, он просто перебирает нужные элементы массива B и заполняет их значениями), в нем присутствуют избыточные источники неэффективности. Предложите другой алгоритм для решения этой задачи с асимптотически лучшим временем выполнения. Другими словами, вы должны разработать алгоритм со временем выполнения O(g(n)), где lim_n→∞g(n)/f(n) = 0.

7. Существует целый класс народных и праздничных песен, в которых каждый куплет представляет собой предыдущий куплет с добавлением одной строки. Например, песня “Двенадцать дней Рождества” обладает этим свойством; добравшись до пятого куплета, вы поете о пяти золотых кольцах, затем упоминаются четыре дрозда из четвертого куплета, три курицы из третьего, две горлицы из второго и, конечно, куропатка из первого. Песня на арамейском языке “Хад гадья”, распеваемая на Пасху, тоже обладает этим свойством, как и многие другие песни.

Обычно такие песни исполняются долго, несмотря на относительно короткий текст. Чтобы определить слова и инструкции для одной из таких песен, достаточно указать новую строку, добавляемую в каждом куплете, не записывая заново все предшествующие строки. (Таким образом, строка “пять золотых колец” будет записана только один раз, хотя она присутствует в пятом и во всех последующих куплетах.)

В этом примере присутствует асимптотическое поведение, которое стоит проанализировать. Для конкретности допустим, что каждая строка имеет длину, ограниченную константой с, и при исполнении песня состоит из n слов. Покажите, как записать слова такой песни в виде текста длиной f(n) для функции f(n) с минимально возможной скоростью роста.

8. Вы занимаетесь экстремальными испытаниями различных моделей стеклянных банок для определения высоты, при падении с которой они не разобьются. Тестовый стенд для этого эксперимента выглядит так: имеется лестница с n ступенями, и вы хотите найти самую высокую ступень, при падении с которой банка останется целой. Назовем ее наивысшей безопасной ступенью.

На первый взгляд естественно применить бинарный поиск: сбросить банку со средней ступени, посмотреть, разобьется ли она, а затем рекурсивно повторить попытку от ступени n/4 или 3n/4 в зависимости от результата. Но у такого решения есть недостаток: вероятно, при поиске ответа будет разбито слишком много банок.

С другой стороны, если вы стремитесь к экономии, можно опробовать следующую стратегию. Сначала банка сбрасывается с первой ступени, потом со второй и т. д. Высота каждый раз увеличивается на одну ступень, пока банка не разобьется. При таком подходе достаточно всего одной банки (как только она разобьется, вы получаете правильный ответ), но для получения ответа может потребоваться до n попыток (вместо log n, как при бинарном поиске).

Похоже, намечается компромисс: можно выполнить меньше попыток, если вы готовы разбить больше банок. Чтобы лучше понять, как этот компромисс работает на количественном уровне, рассмотрим проведение эксперимента с ограниченным “бюджетом” из k ≥ 1 банок. Другими словами, нужно найти правильный ответ (наивысшую безопасную ступень), использовав не более к банок.

(a) Допустим, вам выделен бюджет k = 2 банки. Опишите стратегию поиска наивысшей безопасной ступени, требующую не более f(n) бросков для некоторой функции f(n) с менее чем линейной скоростью роста. (Иначе говоря, в этом случае lim_n→∞f(n)/n = 0.)

(b) Теперь допустим, что доступен бюджет k > 2 банок с некоторым заданным к. Опишите стратегию поиска наивысшей безопасной ступени с использованием не более k банок. Если обозначить количество бросков по вашей стратегии f_k(n), то функции f₁, f₂, f₃, ... должны обладать тем свойством, что каждая из них растет асимптотически медленнее предыдущей: lim_n→∞f_k(n)/f_k-1(n) = 0 для всех k.

Примечания и дополнительная литература

Принятие разрешимости с полиномиальным временем как формального понятия эффективности было постепенным процессом, на который повлияли работы многих исследователей, среди которых были Кобхэм, Рабин, Эдмондс, Хартманис и Стирнс. В отчете Сипсера (Sipser, 1992) содержится как историческая, так и техническая информация по процессу разработки. Подобным образом использование асимптотической записи порядка скорости роста как границы времени выполнения алгоритмов (в отличие от точных формул с коэффициентами при старших членах и младшими членами) было решением, не столь очевидным на момент его введения; в Тьюринговской лекции Тарьяна (Tarjan, 1987) содержится интересная точка зрения на ранние представления исследователей, работавших в этой области, включая Хопкрофта, Тарьяна и других. Дополнительную информацию об асимптотической записи и скорости роста базовых функций можно найти у Кнута (Knuth, 1997а).

Реализация приоритетных очередей с использованием кучи, а также ее применение для сортировки обычно приписываются Уильямсу (Williams, 1964) и Флойду (Floyd, 1964). Приоритетная очередь представляет собой нетривиальную структуру данных с множеством разных применений; в следующих главах мы обсудим другие структуры данных, когда они будут полезны при реализации конкретных алгоритмов. Структура данных Union-Find рассматривается в главе 4 для реализации алгоритма поиска минимального остовного дерева, а рандомизированное хеширование — в главе 13. Другие структуры данных рассматриваются в книге Тарьяна (Tarjan, 1983). Библиотека LEDA (Library of Efficient Datatypes and Algorithms) Мельхорна и Нэера (Mellhorn, Naher, 1999) предоставляет обширную подборку структур данных, используемых в комбинаторных и геометрических задачах.

Примечания к упражнениям

Упражнение 8 основано на задаче, о которой мы узнали от Сэма Туэга.