Более сложная структура данных: приоритетная очередь - Основы анализа алгоритмов

Наша основная цель в этой книге была представлена в начале главы: нас интересуют алгоритмы, обеспечивающие качественный выигрыш по сравнению с поиском методом “грубой силы”; в общем случае этот критерий имеет конкретную формулировку разрешимости с полиномиальным временем. Как правило, нахождение решения нетривиальной задачи с полиномиальным временем не зависит от мелких подробностей реализации, скорее различия между экспоненциальной и полиномиальной сложностью зависят от преодоления препятствий более высокого уровня. Но после разработки эффективного алгоритма решения задачи часто бывает возможно добиться дополнительного улучшения времени выполнения за счет внимания к подробностям реализации, а иногда — за счет использования более сложных структур данных.

Некоторые сложные структуры данных фактически адаптированы для алгоритмов одного определенного типа, другие находят более общее применение. В этом разделе рассматривается одна из самых популярных нетривиальных структур данных — приоритетная очередь. Приоритетные очереди пригодятся для описания реализации некоторых алгоритмов графов, которые будут разработаны позднее в книге. А пока она послужит полезной иллюстрацией к анализу структуры данных, которая, в отличие от списков и массивов, должна выполнять некоторую нетривиальную работу при каждом обращении.

Задача

В реализации алгоритма устойчивых паросочетаний (см. раздел 2.3) упоминалась необходимость поддержания динамически изменяемого множества S (множества всех свободных мужчин в данном примере). В такой ситуации мы хотим иметь возможность добавлять и удалять элементы из S, а также выбрать элемент из S, когда этого потребует алгоритм. Приоритетная очередь предназначена для приложений, в которых элементам назначается приоритет (ключ), и каждый раз, когда потребуется выбрать элемент из S, должен выбираться элемент с наивысшим приоритетом.

Приоритетная очередь представляет собой структуру данных, которая поддерживает множество элементов S. С каждым элементом v ∈ S связывается ключ key(v), определяющий приоритет элемента v; меньшие ключи представляют более высокие приоритеты. Приоритетные очереди поддерживают добавление и удаление элементов из очереди, а также выбор элемента с наименьшим ключом. В нашей реализации приоритетных очередей также будут поддерживаться дополнительные операции, краткая сводка которых приведена в конце раздела.

Основная область применения приоритетных очередей, которая обязательно должна учитываться при обсуждении их общих возможностей, — задача управления событиями реального времени (например, планирование выполнения процессов на компьютере). Каждому процессу присваивается некоторый приоритет, но порядок поступления процессов не совпадает с порядком их приоритетов. Вместо этого имеется текущее множество активных процессов; мы хотим иметь возможность извлечь процесс с наивысшим приоритетом и активизировать его. Множество процессов можно представить в виде приоритетной очереди, в которой ключ процесса представляет величину приоритета. Планирование процесса с наивысшим приоритетом соответствует выбору из приоритетной очереди элемента с наименьшим ключом; параллельно новые процессы должны вставляться в очередь по мере поступления в соответствии со значениями приоритетов.

На какую эффективность выполнения операций с приоритетной очередью можно рассчитывать? Мы покажем, как реализовать приоритетную очередь, которая в любой момент времени содержит не более n элементов, с возможностью добавления и удаления элементов и выбора элемента с наименьшим ключом за время O(log n).

Прежде чем переходить к обсуждению реализации, рассмотрим очень простое применение приоритетных очередей. Оно демонстрирует, почему время O(log n) на операцию является “правильной” границей, к которой следует стремиться.

(2.11) Последовательность из O(n) операций приоритетной очереди может использоваться для сортировки множества из n чисел.

Доказательство. Создадим приоритетную очередь H и вставим каждое число в H, используя его значение в качестве ключа. Затем будем извлекать наименьшие числа одно за другим, пока не будут извлечены все числа; в результате полученная последовательность чисел будет отсортирована по порядку. ■

Итак, с приоритетной очередью, способной выполнять операции вставки и извлечения минимума с временем O(log n) за операцию, можно отсортировать n чисел за время O(n log n). Известно, что в модели вычислений на базе сравнений (при которой каждая операция обращается к входным данным только посредством сравнивания пары чисел) время, необходимое для сортировки, должно быть пропорционально как минимум n log n, так что (2.11) поясняет, что в некотором смысле время O(log n) на операцию — лучшее, на что можно рассчитывать. Следует отметить, что реальная ситуация немного сложнее: реализации приоритетных очередей более сложные, чем представленная здесь, могут улучшать время выполнения некоторых операций и предоставлять дополнительную функциональность. Но из (2.11) следует, что любая последовательность операций приоритетной очереди, приводящая к сортировке n чисел, должна занимать время, пропорциональное по меньшей мере n log n.

Структура данных для реализации приоритетной очереди

Для реализации приоритетной очереди мы воспользуемся структурой данных, называемой кучей (heap). Прежде чем обсуждать организацию кучи, следует рассмотреть, что происходит при более простых, более естественных подходах к реализации функций приоритетной очереди. Например, можно объединить элементы в список и завести отдельный указатель Min на элемент с наименьшим ключом. Это упрощает добавление новых элементов, но с извлечением минимума возникают сложности. Найти минимум несложно (просто перейти по указателю Min), но после удаления минимального элемента нужно обновить Min для следующей операции, а для этого потребуется просканировать все элементы за время O(n) для нахождения нового минимума.

Это усложнение наводит на мысль, что элементы стоило бы хранить в порядке сортировки ключей. Такая структура упростит извлечение элемента с наименьшим ключом, но как организовать добавление новых элементов? Может, стоит хранить элементы в массиве или в связанном списке? Допустим, добавляется элемент s с ключом key(s). Если множество S хранится в отсортированном массиве, можно воспользоваться бинарным поиском для нахождения в массиве позиции вставки s за время O(log n), но для вставки s в массив все последующие элементы необходимо сдвинуть на одну позицию вправо. Сдвиг займет время O(n). С другой стороны, если множество хранится в двусвязном отсортированном списке, вставка в любой позиции выполняется за время O(1), но двусвязный список не поддерживает бинарный поиск, поэтому для поиска позиции вставки s может потребоваться время до O(n).

Определение кучи

Итак, во всех простых решениях по крайней мере одна из операций выполняется за время O(n) — это намного больше времени O(log n), на которое мы надеялись. На помощь приходит куча — структура данных, в нашем контексте сочетающая преимущества сортированного массива и списка. На концептуальном уровне куча может рассматриваться как сбалансированное бинарное дерево (слева на рис. 2.3). У дерева имеется корень, а каждый узел может иметь до двух дочерних узлов: левый и правый. Говорят, что ключи такого бинарного дерева следуют в порядке кучи, если ключ каждого элемента по крайней мере не меньше ключа элемента его родительского узла в дереве. Другими словами,

Порядок кучи: для каждого элемента v в узле i элемент w родителя i удовлетворяет условию key(w) ≤ key(v).

На рис. 2.3 числа в узлах определяют ключи соответствующих элементов.

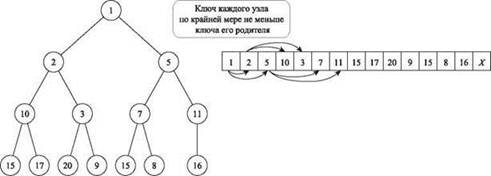
Рис. 2.3. Куча в виде бинарного дерева (слева) и в виде массива (справа). Стрелками обозначены дочерние узлы трех верхних узлов дерева

Прежде чем обсуждать работу с кучей, следует определиться со структурой данных, которая будет использоваться для ее представления. Можно использовать указатели: каждый узел содержит элемент, его ключ и три указателя (два дочерних узла и родительский узел). Однако если заранее известна граница N общего количества элементов, находящихся в куче в любой момент времени, можно обойтись и без указателей. Такие кучи могут храниться в массиве H с индексами i = 1, ..., N. Узлы кучи соответствуют позициям в массиве. H[1] представляет собой корневой узел, а для любого узла в позиции i его дочерние узлы находятся в позициях leftChild(i) = 2i и rightChild(i) = 2i + 1. Таким образом, два дочерних узла корня находятся в позициях 2 и 3, а родитель узла в позиции i находится в позиции parent(i) = [i/2]. Если куча в какой-то момент содержит n < N элементов, то первые n позиций массива используются для хранения n элементов кучи, а количество элементов в H обозначается length(H). С таким представлением куча в любой момент времени является сбалансированной. В правой части рис. 2.3 показано представление в виде массива для кучи, изображенной в левой части.

Реализация операций с кучей

Элементом кучи с наименьшим ключом является ее корень, так что поиск минимального элемента выполняется за время O(1). Как происходит добавление или удаление элементов кучи? Допустим, в кучу добавляется новый элемент v, а куча H на данный момент содержит n < N элементов. После добавления она будет содержать n + 1 элементов. Начать можно с добавления нового элемента v в последнюю позицию i = n + 1, для чего выполняется простое присваивание H[i] = v. К сожалению, при этом нарушается основное свойство кучи, так как ключ элемента vможет быть меньше ключа его родителя. Полученная структура данных почти является кучей, если не считать небольшой “поврежденной” части, где в конце был вставлен элемент v.

Для восстановления кучи можно воспользоваться несложной процедурой. Пусть j = parent(i) = [i/2] является родителем узла i, a H[j] = w. Если key[v] < key[w], позиции v и w просто меняются местами. Перестановка восстанавливает свойство кучи в позиции i, но может оказаться, что полученная структура нарушает свойство кучи в позиции j, — иначе говоря, место “повреждения” переместилось вверх от i к j. Рекурсивное повторение этого процесса от позиции j = parent(i) продолжает восстановление кучи со смещением поврежденного участка вверх.

На рис. 2.4 показаны первые два шага процесса после вставки.

Рис. 2.4. Восходящий процесс восстановления кучи. Ключ 3 в позиции 16 слишком мал (слева). После перестановки ключей 3 и 11 нарушение структуры кучи сдвигается на один шаг к корню дерева (справа)

Чтобы понять, почему эта процедура работает и в конечном итоге приводит к восстановлению порядка, полезно вникнуть структуру “слегка поврежденной” кучи в середине процесса. Допустим, H — массив, а v — элемент в позиции i. Будем называть H псевдокучей со слишком малым ключом H[i], если существует такое значение а ≥ key(v), что повышение key(v) до а приведет к выполнению основного свойства кучи для полученного массива. (Другими словами, элемент v в H[i] слишком мал, но повышение его до а решит проблему.) Важно заметить, что если H является псевдокучей со слишком малым корневым ключом (то есть H[1]), то в действительности H является кучей. Чтобы понять, почему это утверждение истинно, заметим, что если повышение H[1] до а превратит H в кучу, то значение H[1] также должно быть меньше значений обоих его дочерних узлов, — а следовательно, для H уже выполняется свойство порядка кучи.

(2.12) Процедура Heapify-up(H, i) исправляет структуру кучи за время O(log i) при условии, что массив H является псевдокучей со слишком малым ключом H[i]. Использование Heapify-upпозволяет вставить новый элемент в кучу из n элементов за время O(log n).

Доказательство. Утверждение будет доказано методом индукции по i. Если i = 1, истинность очевидна, поскольку, как было замечено ранее, в этом случае H уже является кучей. Теперь рассмотрим ситуацию с i > 1: пусть v = H[i], j = parent(i), w = H[j], и β = key(w). Перестановка элементов v и w выполняется за время O(1). После перестановки массив H представляет собой либо кучу, либо псевдокучу со слишком малым ключом H[j] (теперь содержащим v). Это утверждение истинно, поскольку присваивание в узле j ключа β превращает H в кучу.

Итак, по принципу индукции рекурсивное применение Heapify-up(j) приведет к формированию кучи, как и требовалось. Процесс проходит по ветви от позиции i до корня, а значит, занимает время O(log i).

Чтобы вставить новый элемент в кучу, мы сначала добавляем его как последний элемент. Если новый элемент имеет очень большой ключ, то массив представляет собой кучу. В противном случае перед нами псевдокуча со слишком малым значением ключа нового элемента. Использование процедуры Heapify-up приводит к восстановлению свойства кучи. ■

Теперь рассмотрим операцию удаления элемента. Во многих ситуациях с применением приоритетных очередей не нужно удалять произвольные элементы — только извлекать минимум. В куче это соответствует нахождению ключа в корневом узле (который содержит минимум) с его последующим удалением; обозначим эту операцию ExtractMin(H). Теперь можно реализовать более общую операцию Delete(H, i), которая удаляет элемент в позиции i. Допустим, куча в данный момент содержит n элементов. После удаления элемента H[i] в куче останется n - 1 элементов и помимо нарушения свойства порядка кучи в позиции i возникает “дыра”, потому что элемент H[i] пуст. Начнем с заполнения “дыры” в Hи переместим элемент w из позиции n в позицию i. После этого массив H по крайней мере удовлетворяет требованию о том, что его первые n - 1 элементов находятся в первых n - 1 позициях, хотя свойство порядка кучи при этом может не выполняться.

Тем не менее единственным местом кучи, в котором порядок может быть нарушен, является позиция i, так как ключ элемента w может быть слишком мал или слишком велик для позиции i. Если ключ слишком мал (то есть свойство кучи нарушается между узлом i и его родителем), мы можем использовать Heapify-up(i) для восстановления порядка. С другой стороны, если ключ key[w] слишком велик, свойство кучи может быть нарушено между i и одним или обоими его дочерними узлами. В этом случае будет использоваться процедура Heapify-down, очень похожая на Heapify-up, которая меняет элемент в позиции i с одним из его дочерних узлов и продолжает рекурсивно опускаться по дереву. На рис. 2.5 изображены первые шаги этого процесса.

Рис. 2.5. Нисходящий процесс восстановления кучи. Ключ 21 в позиции 3 слишком велик (слева). После перестановки ключей 21 и 7 нарушение структуры кучи сдвигается на один шаг к низу дерева (справа)

Допустим, H — массив, а w — элемент в позиции i. Будем называть H псевдокучей со слишком большим ключом H[i], если существует такое α ≤ key(w), что понижение key(w) до α приведет к выполнению основного свойства кучи для полученного массива. Если H[i] соответствует узлу кучи (то есть не имеет дочерних узлов) и при этом является псевдокучей со слишком большим ключом H[i], то в действительности H является кучей. В самом деле, если понижение H[i] превратит H в кучу, то значение H[i] уже больше родительского, а следовательно, для H уже выполняется свойство порядка кучи.

(2.13) Процедура Heapify-down(H, i) исправляет структуру кучи за время O(log n) при условии, что массив H является псевдокучей со слишком большим ключом H[i]. Использование Heapify-upили Heapify-down() позволяет удалить новый элемент в куче из n элементов за время O(log n).

Доказательство. Для доказательства того, что этот процесс исправляет структуру кучи, будет использован процесс обратной индукции по значению i. Пусть n — количество элементов в куче. Если 2i > n, то, как было указано выше, H уже является кучей и доказывать ничего не нужно. В противном случае пусть j является дочерним узлом i c меньшим значением ключа, а w = H[j]. Перестановка элементов массива w и v выполняется за время O(1). После перестановки массив H представляет собой либо кучу, либо псевдокучу со слишком большим ключом H[j] = v. Это утверждение истинно, поскольку присваивание key(v) = key(w) превращает H в кучу. Теперь j ≥ 2i, поэтому по предположению индукции рекурсивный вызов Heapify-down восстанавливает свойство кучи.

Алгоритм многократно перемещает элемент, находящийся в позиции i, вниз по ветви, поэтому за O(log n) итераций будет сформирована куча.

Чтобы использовать этот процесс для удаления элемента v = H[i] из кучи, мы заменяем H[i] последним элементом массива, H[n] = w. Если полученный массив не является кучей, то это псевдокуча со слишком малым или слишком большим значением ключа H[i]. Использование процедуры Heapify-up или Heapify-down приводит к восстановлению свойства кучи за время O(log n). ■

Реализация приоритетной очереди на базе кучи

Структура данных кучи с операциями Heapify-down и Heapify-up позволяет эффективно реализовать приоритетную очередь, которая в любой момент времени содержит не более N элементов. Ниже приводится сводка операций, которые мы будем использовать.

♦ StartHeap(N) возвращает пустую кучу H, настроенную для хранения не более N элементов. Операция выполняется за время O(N), так как в ней инициализируется массив, используемый для хранения кучи.

♦ Insert(H, v) вставляет элемент v в кучу H. Если куча в данный момент содержит n элементов, операция выполняется за время O(log n).

♦ FindMin(H) находит наименьший элемент кучи H, но не удаляет его. Операция выполняется за время O(1).

♦ Delete(H, i) удаляет элемент в позиции i. Для кучи, содержащей n элементов, операция выполняется за время O(log n).

♦ ExtractMin(H) находит и удаляет из кучи элемент с наименьшим значением ключа. Она объединяет две предыдущие операции, а следовательно, выполняется за время O(log n).

Также существует второй класс операций, которые должны выполняться с элементами по имени, а не по их позиции в куче. Например, во многих алгоритмах графов, использующих структуру данных кучи, элементы кучи представляют узлы графа, ключи которых вычисляются в процессе выполнения алгоритма. В разных точках этого алгоритма операция должна выполняться с некоторым узлом независимо от того, где он находится в куче.

Чтобы организовать эффективное обращение к нужным элементам приоритетной очереди, достаточно создать дополнительный массив Position, в котором хранится текущая позиция каждого элемента (каждого узла графа) в куче. С ним можно реализовать следующие операции.

♦ Для удаления элемента v применяется операция Delete(H,Position[v]). Создание массива не увеличивает общее время выполнения, поэтому удаление элемента v из кучи с n узлами выполняется за время O(log n).

♦ В некоторых алгоритмах также используется операция ChangeKey(H, v, α), которая изменяет ключ элемента v новым значением key(v) = α. Чтобы реализовать эту позицию за время O(log n), необходимо сначала определить позицию v в массиве, что делается при помощи массива Position. После определения позиции элемента v мы изменяем его ключ, а затем применяем процедуру Heapify-up или Heapify-down в зависимости от ситуации.