Алгоритмы - Разработка и применение - 2016 год
Кластеризация - Жадные алгоритмы
Практическая ценность задачи нахождения минимального остовного дерева была продемонстрирована на примере построения низкозатратной сети, связывающей ряд географических точек. Однако минимальные остовные деревья возникают во многих других ситуациях, порой внешне не имеющих ничего общего. Интересный пример использования минимальных остовных деревьев встречается в области кластеризации.
Задача
Под задачей кластеризации обычно понимается ситуация, в которой некую коллекцию объектов (допустим, набор фотографий, документов, микроорганизмов и т. д.) требуется разделить на несколько логически связных групп. В такой ситуации естественно начать с определения метрик сходства или расхождения каждой пары объектов. Одно из типичных решений основано на определении функции расстояния между объектами; предполагается, что объекты, находящиеся на большем расстоянии друг от друга, в меньшей степени похожи друг на друга. Для точек в реальном мире расстояние может быть связано с географическим расстоянием, но во многих случаях ему приписывается более абстрактный смысл. Например, расстояние между двумя биологическими видами может измеряться временным интервалом между их появлением в ходе эволюции; расстояние между двумя изображениями в видеопотоке может измеряться количеством пикселов, в которых интенсивность цвета превышает некоторый порог.
Для заданной функции расстояния между объектами процесс кластеризации пытается разбить их на группы так, чтобы объекты одной группы интуитивно воспринимались как “близкие”, а объекты разных групп — как “далекие”. Этот несколько туманный набор целей становится отправной точкой для множества технически различающихся методов, каждый из которых пытается формализовать общее представление о том, как должен выглядеть хороший набор групп.
Кластеризация по максимальному интервалу
Минимальные остовные деревья играют важную роль в одной из базовых формализаций, которая будет описана ниже. Допустим, имеется множество U из n объектов р1, p2, ..., pn. Для каждой пары pi и рj, определяется числовое расстояние d(pi, pj). К функции расстояния предъявляются следующие требования: d(pi, pj) = 0; d(pi, pj) > 0 для разных рi и рj, а также d(pi, pj) = d(pj, pi) (симметричность).
Предположим, объекты из U требуется разделить на k групп для заданного параметра k. Термином “k-кластеризация U” обозначается разбиение U на k непустых множеств С1, C2, ..., Сk. “Интервалом k-кластеризации” называется минимальное расстояние между любой парой точек, находящихся в разных кластерах. С учетом того, что точки разных кластеров должны находиться далеко друг от друга, естественной целью является нахождение k-кластеризации с максимально возможным интервалом.
Мы приходим к следующему вопросу. Количество разных k-кластеризаций множества U вычисляется по экспоненциальной формуле; как эффективно найти кластеризацию с максимальным интервалом?
Разработка алгоритма
Чтобы найти кластеризацию с максимальным интервалом, мы рассмотрим процедуру расширения графа с множеством вершин U. Компоненты связности соответствуют кластерам, и мы постараемся как можно быстрее объединить близлежащие точки в один кластер (чтобы они не оказались в разных кластерах, находящихся поблизости друг от друга). Начнем с создания ребра между ближайшей парой точек; затем создается ребро между парой точек со следующей ближайшей парой и т. д. Далее мы продолжаем добавлять ребра между парами точек в порядке увеличения расстояния d(pi, pj).
Таким образом граф H с вершинами U наращивает ребро за ребром, при этом компоненты связности соответствуют кластерам. Учтите, что нас интересуют только компоненты связности графа H, а не полное множество ребер; если при добавлении ребра (pi, pj) выяснится, что pi и pj уже принадлежат одному кластеру, ребро добавляться не будет — это не нужно, потому что ребро не изменит множество компонент. При таком подходе в процессе расширения графа никогда не образуется цикл, так что H будет объединением деревьев. Добавление ребра, концы которого принадлежат двум разным компонентам, фактически означает слияние двух соответствующих кластеров. В литературе по кластеризации подобный итеративный процесс слияния кластеров называется методом одиночной связи — частным случаем иерархической агломератной кластеризации. (Под “агломератностью” здесь понимается процесс объединения кластеров, а под “одиночной связью” — то, что для объединения кластеров достаточно одной связи.) На рис. 4.14 изображен пример для k = 3 кластеров с разбиением точек на естественные группы.
Какое отношение все это имеет к минимальным остовным деревьям? Очень простое: хотя процедура расширения графа базировалась на идее слияния кластеров, она в точности соответствует алгоритму минимального остовного дерева Крускала. Делается в точности то, что алгоритм Крускала сделал бы для графа G, если бы между каждой парой узлов (pi, pj) существовало ребро стоимостью d(pi, pj). Единственное отличие заключается в том, что мы стремимся выполнить k-кластеризацию, поэтому процедура останавливается при получении к компонент связности.
Другими словами, выполняется алгоритм Крускала, но он останавливается перед добавлением последних k - 1 ребер. Происходящее эквивалентно построению полного минимального остовного дерева T (в том виде, в каком оно было бы построено алгоритмом Крускала), удалению k - 1 ребер с наибольшей стоимостью (которое наш алгоритм вообще не добавлял) и определению k-кластеризации по полученным компонентам связности C1, C2,..., Ck. Итак, итеративное слияние кластеров эквивалентно вычислению минимального остовного дерева с удалением самых “дорогостоящих” ребер.
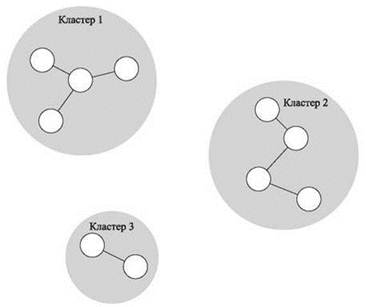
Рис. 4.14. Пример кластеризации методом одиночной связи с k = 3 кластерами. Кластеры образуются добавлением ребер между точками в порядке увеличения расстояния
Анализ алгоритма
Удалось ли нам достичь своей цели — создать кластеры, разделенные максимально возможным интервалом? Следующее утверждение доказывает этот факт.
(4.26) Компоненты C1, C2, ..., Ck, образованные удалением k - 1 ребер минимального остовного дерева T с максимальной стоимостью, образуют k-кластеризацию с максимальным интервалом.
Доказательство. Пусть C — кластеризация C1, C2, ..., Ck. Интервал C в точности равен длине d * (k - 1)-го ребра с максимальной стоимостью в минимальном остовном дереве; это длина ребра, которое алгоритм Крускала добавил бы на следующем шаге (в тот момент, когда мы его остановили).
Возьмем другую k-кластеризацию C', которая разбивает U на непустые множества C'1, C'2, ..., C'k. Требуется показать, что интервал C' не превышает d*.
Так как две кластеризации C и C' не совпадают, из этого следует, что один из кластеров Cr не является подмножеством ни одного из k множеств C's в C'. Следовательно, должны существовать точки рi, pj ∈ Cr, принадлежащие разным кластерам в C', — допустим, pi ∈ C's и рj ∈ C't ≠ C's.
Теперь взгляните на рис. 4.15. Так как рi и рj принадлежат одной компоненте С, алгоритм Крускала должен был добавить все ребра рi-рj пути P перед его остановкой. В частности, это означает, что длина каждого ребра P не превышает d*. Мы знаем, что рi ∈ C's, но рj ∉ C'; пусть р' — первый узел P, который не принадлежит C's, а р — узел из P, непосредственно предшествующий р'. Только что было замечено, что d(р, р') ≤ d*, так как ребро (р, р') было добавлено алгоритмом Крускала. Но р и р' принадлежат разным множествам кластеризации С', а значит, интервал С' не превышает d(р, р') ≤ d*, что и завершает доказательство. ■
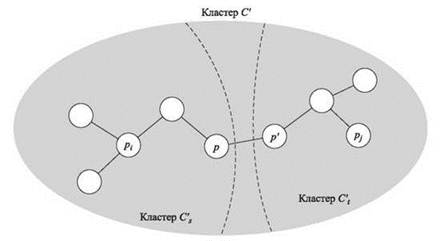
Рис. 4.15. Иллюстрация доказательства (4.26), показывающая, что интервал никакой другой кластеризации не может быть больше интервала кластеризации, найденной алгоритмом одиночной связи