Коды Хаффмана и сжатие данных - Жадные алгоритмы

В задачах нахождения кратчайшего пути и минимального остовного дерева было показано, как жадные алгоритмы позволяют ограничиться определенными частями решения (ребрами графа в этих случаях), основываясь исключительно на относительно “недальновидных” соображениях. А сейчас будет рассмотрена задача, в которой “ограничение” понимается еще свободнее: по сути, жадное правило используется для сокращения размера экземпляра задачи, чтобы эквивалентную меньшую задачу можно было решить посредством рекурсии. Будет доказано, что такая жадная операция “безопасна” в том смысле, что решение меньшего экземпляра приводит к оптимальному решению исходной задачи, однако глобальные последствия исходного жадного решения проявляются только при завершении полной рекурсии.

Сама задача относится к одной из базовых тем из области сжатия данных — области, формирующей технологическую основу цифровой передачи данных.

Задача

Компьютеры в конечном счете работают с последовательностями битов (то есть последовательностями, состоящими только из 0 и 1), поэтому должна существовать некая схема кодирования, которая берет текст, написанный на более полном алфавите (например, алфавите одного из мировых языков), и преобразует его в длинную цепочку битов.

Самое простое решение — использовать фиксированное число битов для каждого символа в алфавите, а затем просто объединить цепочки битов для каждого символа. Рассмотрим простой пример: допустим, мы хотим закодировать 26 букв английского языка, а также пробел (для разделения слов) и пять знаков препинания: запятую, точку, вопросительный знак, восклицательный знак и апостроф. Таким образом, закодировать нужно 32 символа. Из b битов можно сформировать 2^b разных последовательностей, поэтому при использовании 5 битов на символ можно закодировать 2⁵ = 32 символа — вполне достаточно для наших целей. Например, цепочка битов 00000 будет представлять букву “a”, цепочка 00001 — букву “b”, и т. д. вплоть до цепочки 11111, которая представляет апостроф. Следует учитывать, что соответствие битовых цепочек и символов выбирается произвольно; суть в том, что пяти битов на символ достаточно. Такие схемы кодирования, как ASCII, работают именно так, не считая того, что они используют больше количество битов на символ для поддержки наборов с большим количеством символов, включая буквы верхнего регистра, скобки и все специальные символы, которые вы видите на клавиатуре пишущей машинки или компьютера.

Вернемся к простейшему примеру с 32 символами. Какие еще требования могут предъявляться к схеме кодирования? Ограничиться 4 битами на символ не удастся, потому что 2⁴ = 16 — недостаточно для имеющегося количества символов. С другой стороны, неочевидно, что в больших объемах текста код одного символа в среднем должен состоять из 5 битов. Если задуматься, буквы большинства алфавитов используются с разной частотой. Скажем, в английском языке буквы e, t, a, o, i и n используются намного чаще букв q, j, x и z (более чем на порядок). Получается, что кодировать их одинаковым количеством битов крайне расточительно; разумнее было бы использовать малое количество битов для часто встречающихся букв, а большее количество битов для редких букв и надеяться на то, что в длинных блоках типичного текста для представления одной буквы в среднем будет использоваться менее 5 бит.

Сокращение среднего количества битов на символ является одной из фундаментальных задач в области сжатия данных. Когда большие файлы нужно передать по коммуникационной сети или сохранить на жестком диске, важно найти для них как можно более компактное представление — при условии, что сторона, которая будет читать файл, сможет правильно восстановить его. Значительные объемы исследований были посвящены разработке алгоритмов сжатия, которые получают файлы и сокращают объем занимаемого ими пространства за счет применения эффективных схем кодирования.

А теперь мы рассмотрим одну из фундаментальных формулировок этой задачи, через которую мы постепенно придем к вопросу о том, как оптимальным образом использовать факт неравномерности относительных частот букв. В каком-то смысле такое оптимальное решение становится хорошим ответом для задачи сжатия данных: из неравномерности частот извлекается вся возможная польза. В завершающей части этого раздела речь пойдет о том, как повысить эффективность сжатия за счет использования других возможностей помимо неравномерности частот.

Схемы кодирования с переменной длиной

До появления Интернета, цифровых компьютеров, радио и телефона существовал телеграф. По телеграфу данные передавались намного быстрее, чем в современных ему альтернативах доставки (железная дорога или лошади). Но телеграф позволял передавать по проводу только электрические импульсы, поэтому для передачи сообщения необходимо каким-то образом закодировать текст сообщения в виде последовательности импульсов.

Пионер телеграфной передачи данных Сэмюэл Морзе разработал код, в котором каждая буква соответствовала серии точек (короткие импульсы) и тире (длинные импульсы). В нашем контексте точки и тире можно заменить нулями и единицами, так что задача сводится к простому отображению символов на цепочки битов, как и в кодировке ASCII. Морзе понимал, что эффективность передачи данных можно повысить за счет кодирования более частых символов короткими строками, и выбрал именно такое решение. (За информацией об относительных частотах букв английского языка он обратился к местным типографиям.) В коде Морзе букве “e” соответствует 0 (точка), букве “t” — 1 (тире), букве “а” — 01 (точка-тире), и вообще более частым буквам соответствуют более короткие цепочки.

В коде Морзе для представления букв используются настолько короткие цепочки, что кодирование слов становится неоднозначным. Например, из того, что мы знаем о кодировке букв “е”, “t” и “а”, становится видно, что цепочка 0101 может соответствовать любой из последовательностей “eta”, “аа”, “etet” или “aet”. (Также существуют другие возможные варианты с другими буквами.) Для разрешения этой неоднозначности при передаче кода Морзе буквы разделяются короткими паузами (так что текст “аа” будет кодироваться последовательностью точка-тире- пауза-точка-тире-пауза). Это решение — очень короткие битовые цепочки с паузами — выглядит разумно, но оно означает, что буквы кодируются не 0 и 1; фактически применяется алфавит из трех букв — 0, 1 и “пауза”. Следовательно, если потребуется что-то закодировать только битами 0 и 1, потребуется дополнительное кодирование, которое ставит в соответствие паузе последовательность битов.

Префиксные коды

Проблема неоднозначности в коде Морзе возникает из-за существования пар букв, у которых битовая цепочка, кодирующая одну букву, является префиксом в битовой цепочке, кодирующей другую букву. Чтобы устранить эту проблему (а следовательно, получить схему кодирования с четко определенной интерпретацией каждой последовательности битов), достаточно отображать буквы на цепочки битов так, чтобы ни одна кодовая последовательность не была префиксом другой кодовой последовательности.

Префиксным кодом для множества букв S называется функция у, которая отображает каждую букву x ∈ S на некую последовательность нулей и единиц так, что для разных x, y ∈ Sпоследовательность γ(x) не является префиксом последовательности γ(y).

Предположим, имеется текст, состоящий из последовательности букв x₁, x₂, x₃, ..., x_n. Чтобы преобразовать его в последовательность битов, достаточно закодировать каждую букву последовательностью битов с использованием у, а затем объединить все эти последовательности: γ(x₁)γ(x₂)..:γ(x_n). Если это сообщение передается получателю, которому известна функция у, то получатель сможет восстановить текст по следующей схеме:

♦ Просканировать последовательность битов слева направо.

♦ Как только накопленных битов будет достаточно для кодирования некоторой буквы, вывести ее как первую букву текста. Ошибки исключены, потому что никакой более короткий или длинный префикс последовательности битов не может кодировать никакую другую букву.

♦ Удалить соответствующую последовательность битов от начала сообщения и повторить сначала.

В этом случае получатель сможет получить правильную последовательность букв, не прибегая к искусственным мерам вроде пауз для разделения букв. Предположим, мы пытаемся закодировать набор из пяти букв S ={a, b, c, d, e}. Кодировка γ₁, заданная следующим образом:

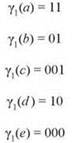
является префиксным кодом, поскольку ни один код не является префиксом другого. Например, строка “cecab” будет закодирована в виде 0010000011101. Получатель, зная γ₁, начнет читать сообщение слева направо.

Ни 0, ни 00 не являются кодом буквы, но для 001 такое соответствие обнаруживается, и получатель приходит к выводу, что первой буквой является “c”. Такое решение безопасно, поскольку ни одна более длинная последовательность битов, начинающаяся с 001, не может обозначать другую букву. Затем получатель перебирает остаток сообщения, 0000011101; он приходит к выводу, что второй буквой является “e” (000), и т. д.

Оптимальные префиксные коды

Все это делается из-за того, что некоторые буквы встречаются чаще других и мы хотим воспользоваться тем обстоятельством, что более частые буквы можно кодировать более короткими последовательностями. Чтобы точно сформулировать эту цель, сейчас мы введем вспомогательные обозначения для выражения частот букв.

Предположим, для каждой буквы х ∈ S существует относительная частота f_x, представляющая долю в тексте букв, равных х. Другими словами, если текст состоит из n букв, то nf_x из этих букв равны х. Сумма всех относительных частот равна 1, то есть

Если префиксный код у используется для кодирования заданного текста, то какой будет общая длина кодирования? Она будет равна сумме (по всем буквам х ∈ S) количества вхождений х, умноженной на длину битовой цепочки γ(х), используемой для кодирования х. Если |γ(х)| обозначает длину γ(х), этот факт можно записать в виде

Исключая коэффициент n из последнего выражения, получаем ^— среднее количество битов, необходимых для представления буквы. В дальнейшем эта величина обозначается ABL(γ) (Average Bits per Letter).

В продолжение этого примера допустим, что имеется текст с буквами S = {a, b, c, d, e} и следующим набором относительных частот:

Тогда среднее количество битов на букву для префиксного кода γ₁, определенного ранее, составит

Интересно сравнить эту величину со средним количеством битов на букву при использовании кодировки с фиксированной длиной. (Заметьте, что кодировка с фиксированной длиной является префиксным кодом: если все буквы кодируются последовательностями одинаковой длины, то никакой код не может быть префиксом любого другого.) Очевидно, в множестве S из пяти букв для кодировки с фиксированной длиной понадобится три бита на букву, так как два бита позволят закодировать только четыре буквы. Следовательно, кодировка γ₁ сокращает количество битов на букву с 3 до 2,25 — экономия составляет 25 %.

На самом деле γ₁ не лучшее, что можно сделать в этом примере. Рассмотрим префиксный код γ₂, определяемый следующим образом:

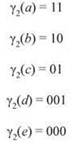
Среднее количество битов на букву для γ₂ составит

Теперь можно сформулировать естественный вопрос. Для заданного алфавита и множества относительных частот букв нам хотелось бы получить префиксный код, обладающий наибольшей эффективностью, а именно префиксный код, минимизирующий среднее количество битов на букву Такой префиксный код называется оптимальным.

Разработка алгоритма

Пространство поиска в этой задаче весьма сложно: оно включает все возможные способы отображения букв на цепочки битов с учетом определяющего свойства префиксных кодов. Для алфавитов с очень малым количеством букв возможен перебор этого пространства методом “грубой силы”, но такой подход быстро становится неприемлемым.

А теперь будет описан жадный метод построения оптимального префиксного кода с высокой эффективностью. Полезно начать с создания способа представления префиксных кодов на базе дерева, который репрезентирует их структуру более четко, чем списки значений из предыдущих примеров.

Представление префиксных кодов в форме бинарных деревьев

Дерево T, в котором каждый узел, не являющийся листовым, имеет не более двух дочерних узлов, называется бинарным деревом. Допустим, количество листовых узлов равно размеру алфавита S, а каждый лист помечен одной из букв S.

Такое бинарное дерево T естественно описывает префиксный код. Для каждой буквы х ∈ S отслеживается путь от корня до листа с меткой х; каждый раз, когда путь переходит от узла к его левому дочернему узлу, в результирующую цепочку битов записывается 0, а при переходе к правому узлу — 1. Полученная цепочка битов рассматривается как кодировка х.

Отметим следующий факт:

(4.27) Кодировка алфавита S, построенная на основе T, представляет собой префиксный код.

Доказательство. Чтобы кодировка х была префиксом кодировки у, путь от корня к узлу х должен быть префиксом пути от корня к узлу у. Но для этого узел х должен лежать на пути от корня к у, а это невозможно, если узел х является листовым. ■

Отношения между бинарными деревьями и префиксными кодами также работают и в обратном направлении: для префиксного кода γ можно рекурсивно построить бинарное дерево. Начните с корня; все буквы х ∈ S, кодировка которых начинается с 0, будут представлены листовыми узлами в левом поддереве, а все буквы y ∈ S, кодировка которых начинается с 1, будут представлены листьями в правом поддереве. Далее эти два поддерева строятся рекурсивно по указанному правилу.

Например, дерево на рис. 4.16, а соответствует следующему префиксному коду γ₀:

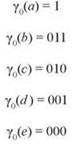
Чтобы убедиться в этом, заметьте, что к листу с меткой а можно перейти, просто выбрав правую ветвь от корневого узла (кодировка 1); для перехода к узлу e следует трижды выбрать левую ветвь от корневого узла; такие же объяснения действуют для b, c и d. Аналогичные рассуждения показывают, что дерево на рис. 4.16, b соответствует префиксному коду γ₁, а дерево на рис. 4.16, c соответствует префиксному коду γ₂ (оба кода определялись выше). Также следует заметить, что бинарные деревья двух префиксных кодов γ₁ и γ₂ имеют идентичную структуру; различаются только метки листьев. С другой стороны, дерево Y₀ имеет отличающуюся структуру.

Таким образом, поиск оптимального префиксного кода может рассматриваться как нахождение бинарного дерева T в сочетании с пометкой узлов T, минимизирующей среднее количество битов на букву. Кроме того, эта средняя величина имеет естественную интерпретацию в контексте структуры T: длина кодировки буквы х ∈ S попросту равна длине пути от корневого узла до листа с меткой х. Длина пути будет называться глубиной листа, а глубина листа v в T будет обозначаться depth_T(v). (Для удобства записи мы будем опускать нижний индекс T там, где он очевиден из контекста, и часто будем использовать букву х ∈ S для обозначения помечаемого ею узла.) Итак, мы пытаемся найти дерево с метками узлов, обладающее минимальным средним значением глубин всех листьев, взвешенных по частотам букв, которыми помечены листья: Для обозначения этой метрики будет использоваться запись ABL(T).

Первым шагом рассмотрения алгоритмов для этой задачи станет констатация простого факта, относящегося к оптимальному дереву. Для этого нам понадобится вспомогательное определение: бинарное дерево называется полным, если каждый узел, который не является листовым, имеет два дочерних узла. (Другими словами, не существует узлов, имеющих ровно один дочерний узел.) Обратите внимание: все три бинарных дерева на рис. 4.16 являются полными.

(4.28) Бинарное дерево, соответствующее оптимальному префиксному коду, является полным.

Рис. 4.16. Три разных префиксных кода для алфавита S = {a, b, c, d, e}

Доказательство. Это утверждение легко доказывается методом замены. Пусть T — бинарное дерево, соответствующее оптимальному префиксному коду; допустим, оно содержит узел u, имеющий ровно один дочерний узел v. Преобразуем T в дерево T', заменив узел u узлом v.

Чтобы анализ был точным, необходимо различать два случая. Если u — корень дерева, узел u просто удаляется, а v используется в качестве корневого узла. Если u корнем не является, пусть wявляется родителем u в T. В этом случае u удаляется, а v становится дочерним узлом w вместо u. Это изменение уменьшает количество битов, необходимых для кодирования любого листа в поддереве, корнем которого является u, и не влияет на другие листья. Итак, префиксный код, соответствующий T', имеет меньшее среднее количество битов на букву, чем префиксный код T, а это противоречит предположению об оптимальности T. ■

Первая попытка: нисходящий метод

На интуитивном уровне мы стремимся построить размеченное бинарное дерево, листья которого должны располагаться как можно ближе к корню. Именно такое строение обеспечит наименьшую среднюю глубину листа.

Естественный подход к решению этой задачи будет основан на построении дерева сверху вниз с как можно более плотной “упаковкой” листьев. Допустим, мы пытаемся разбить алфавит S на два множества S₁ и S₂, так, чтобы сумма частот букв в каждом наборе была равна в точности 1/2. Если такое идеальное разбиение невозможно, то мы можем опробовать следующую разбивку, ближайшую к сбалансированности. Затем для S₁ и S₂ рекурсивно строятся префиксные коды, которые образуют два поддерева от корневого узла. (В контексте цепочек битов это означает, что кодировки для S_l будут начинаться с 0, а кодировки для S₂ — с 1.)

Пока не совсем ясно, как конкретно определить это “почти сбалансированное” разбиение алфавита, однако более точная формулировка возможна. Такие схемы кодирования называются кодами Шеннона-Фано по именам Клода Шеннона и Роберта Фано — двух крупных ученых, работавших в области теории передачи информации (дисциплины, изучающей способы представления и кодирования цифровых данных). Такие префиксные коды неплохо работают на практике, но для наших текущих целей они создают своего рода “тупик”: никакая разновидность такой стратегии нисходящего разбиения не будет гарантированно создавать оптимальный префиксный код. Вернемся к примеру с алфавитом из пяти букв S = {a, b, c, d, e} и частотами

Существует всего один способ разбиения этого алфавита на два множества с равными частотами: {a, d} и {b, c, e}. В подмножестве {a, d} каждая буква может кодироваться одним дополнительным битом. Для {b, c, e} кодирование должно продолжаться рекурсивно, и снова существует уникальный способ разбиения множества на два подмножества с равной суммой частот. Полученный код соответствует кодировке γ₁, представленной размеченным деревом на рис. 4.16, b; как вы уже знаете, кодировка γ₁ менее эффективна, чем префиксная кодировка γ₂, соответствующая дереву на рис. 4.16, c.

Шеннон и Фано знали, что их метод не всегда порождает оптимальный префиксный код, но не знали, как вычислить оптимальный код без поиска методом “грубой силы”. Эту задачу через несколько лет решил аспирант Дэвид Хаффман — он узнал о задаче на учебном курсе, который вел Фано.

Рассмотрим некоторые идеи, которые привели Хаффмана к обнаружению жадного алгоритма построения оптимальных префиксных кодов.

А если бы структура дерева оптимального префиксного кода была известна?

Существует метод, который часто помогает при поиске эффективного алгоритма: вы мысленно предполагаете, что у вас имеется частичная информация об оптимальном решении, и смотрите, как воспользоваться этой неполной информацией для поиска полного решения. (Как будет показано позднее, в главе 6, этот метод является одной из главных основ метода динамического программирования при разработке алгоритмов.)

В контексте текущей задачи будет полезно задаться вопросом: а если бы нам было известно бинарное дерево T*, соответствующее оптимальному префиксному коду, но не разметка листьев? Осталось бы разобраться, какой буквой должен быть помечен каждый из листьев T*, и код был бы найден. Насколько сложно это сделать?

На самом деле это достаточно просто, но сначала следует сформулировать базовый факт.

(4.29) Допустим, u и v — листовые узлы T*, такие что depth(u) < depth(v). Также предположим, что в разметке T*, соответствующей оптимальному префиксному коду, лист u помечается y ∈ S, а лист v помечается z ∈ S. В этом случае f_y ≥ f_z.

Доказательство. Следующее короткое доказательство основано на методе замены. Допустим, f_y < f_z; рассмотрим код, который будет получен, если поменять местами метки узлов u и v. В выражении для среднего количества битов на букву замена приводит к следующему эффекту: множитель у f_y возрастает (с depth(u) до depth(v)), а множитель у f_zуменьшается на ту же величину (с depth(v) до depth(u)). Следовательно, сумма изменится на величину (depth(v) - depth(u))(f_y - f_z). Если f_y < f_z, это изменение будет отрицательным числом, что противоречит предположению об оптимальности префиксного кода до замены. ■

Идея, заложенная в основу (4.29), продемонстрирована на рис. 4.16, b. Как легко показать, что код неоптимален? Достаточно показать, что его можно улучшить, поменяв местами метки c и d. Наличие низкочастотной буквы на строго меньшей глубине, чем у другой буквы с более высокой частотой, — именно тот признак, который исключается у оптимального решения согласно (4.29).

Из (4.29) следует интуитивно понятный оптимальный способ разметки готового дерева T* (при условии, что кто-то нам его предоставил). Сначала берем все листья глубины 1 (если они есть) и размечаем их буквами с наибольшей частотой в любом порядке. Затем берем все листья глубины 2 (если они есть) и размечаем их буквами с наибольшей частотой в любом порядке. Процедура продолжается в порядке повышения глубины, с назначением букв в порядке уменьшения частоты. Здесь важно то, что это не может привести к субоптимальной разметке T*, поскольку к любой предположительно лучшей разметке может быть применена замена (4.29). Также принципиально то, что при назначении меток в блоке листьев одной глубины не важно, какая метка будет назначена тому или иному узлу. Поскольку глубины совпадают, соответствующие множители в выражении тоже совпадают, а выбор присваивания между листьями одной глубины не влияет на среднее количество битов на букву.

Но как все это поможет нам? Структура оптимального дерева T* нам неизвестна, а из-за экспоненциального количества возможных деревьев (от размера алфавита) перебрать все возможные деревья методом “грубой силы” не удастся.

Однако все рассуждения о T* становятся очень полезными, если думать не о начале процесса разметки (с листьями минимальной глубины), а о его завершении с листьями максимальной глубины — теми, которым достаются буквы с наименьшей частотой. А конкретнее, рассмотрим лист v в дереве T* с наибольшей возможной глубиной. Лист v имеет родителя и, но, согласно (4.28), T* является полным бинарным деревом, поэтому у и есть другой дочерний узел — w. Узлы v и w будут называться одноранговыми (или соседями). Тогда получаем

(4.30) Узел w является листом T*.

Доказательство. Если узел w не является листовым, где-то в поддереве ниже него должен быть узел w'. Но тогда глубина w' будет превышать глубину v, а это противоречит нашему предположению о том, что v является листом максимальной глубины в T*. ■

Итак, v и w — одноранговые узлы, имеющие максимально возможную глубину в T*. Следовательно, процесс разметки T* в соответствии с (4.29) доберется до уровня, содержащего v и w, в последнюю очередь. Для этого уровня останутся буквы с наименьшей частотой. Так как порядок назначения этих букв листьям внутри уровня роли не играет, существует оптимальная разметка, при которой v и w достанутся две буквы с наименьшей частотой из всех возможных.

Подведем итог:

(4.31) Существует оптимальный префиксный код с соответствующим деревом T*, в котором две буквы с наименьшей частотой назначаются листьям, которые являются одноранговыми в T*.

Алгоритм построения оптимального префиксного кода

Предположим, у* и z* — две буквы S с наименьшими частотами (с произвольной разбивкой “ничьих”). Утверждение (4.31) важно, так как оно сообщает важную информацию о местонахождении у* и z* в оптимальном решении; оно говорит, что при анализе решениях их можно “держать вместе”, потому что мы знаем, что они станут одноранговыми узлами под общим родителем. Получается, что этот общий родитель становится “метабуквой”, частота которой равна сумме частот у* и z*.

Отсюда напрямую следует идея алгоритма: у* и z* заменяются этой метабуквой с получением алфавита, уменьшенного на одну букву. Затем рекурсивно вычисляется префиксный код для сокращенного алфавита, метабуква снова “раскрывается” на у* и z* с получением префиксного кода для S. Эта рекурсивная стратегия изображена на рис. 4.17.

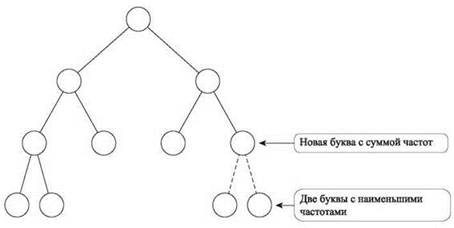
Рис. 4.17. Существует оптимальное решение, в котором две буквы с наименьшими частотами используются для пометки одноранговых листьев; если удалить их и пометить родительский узел новой буквой с суммарной частотой, это порождает экземпляр задачи с сокращенным алфавитом

Ниже приводится формальное описание алгоритма.

Эта процедура будет называться алгоритмом Хаффмана, а префиксный код, создаваемый ею для заданного алфавита, соответственно, будет называться кодом Хаффмана. В общем случае очевидно, что выполнение алгоритма всегда завершается, потому что он рекурсивно вызывает себя для алфавита, уменьшенного на одну букву. Более того, с (4.31) нетрудно доказать, что алгоритм действительно создает оптимальный префиксный код. Но перед этим стоит сделать пару замечаний по поводу алгоритма.

Для начала рассмотрим поведение алгоритма на примере с S = {a, b, c, d, e} и частотами

Алгоритм объединяет d и e в одну букву — обозначим ее (de) — с частотой 0,18 + 0,05 = 0,23. Теперь мы имеем экземпляр задачи с четырехбуквенным алфавитом S' = {a, b, c, (de)}. Двумя буквами S' с наименьшей частотой являются буквы c и (de), поэтому на следующем шаге они объединяются в одну букву (cde) с частотой 0,20 + 0,23 = 0,43; образуется трехбуквенный алфавит {a, b, (cde)}. Далее объединяются буквы a и b с получением алфавита из двух букв, и в этой точке активизируется база рекурсии. Развернув результат по цепочке рекурсивных вызовов, мы получим дерево, изображенное на рис. 4.16, c.

Интересно, как жадное правило, заложенное в основу алгоритма Хаффмана (слияние букв с двумя наименьшими частотами), укладывается в структуру алгоритма в целом. Фактически на момент слияния двух букв мы не знаем точно, какое место они займут в общем коде. Вместо этого мы просто считаем их дочерними узлами одного родителя, и этого хватает для построения новой эквивалентной задачи, сокращенной на одну букву.

Кроме того, алгоритм образует естественный контраст с более ранним решением, приводящим к субоптимальным кодам Шеннона-Фано. Этот метод базировался на нисходящей стратегии, которая прежде всего обращала внимание на разбиение верхнего уровня в бинарном дереве, а именно на два подузла, находящиеся непосредственно под корнем. С другой стороны, алгоритм Хаффмана использует восходящий метод: он находит листья, представляющие две буквы с самой низкой частотой, а затем продолжает работу по рекурсивному принципу.

Анализ алгоритма

Оптимальность

Начнем с доказательства оптимальности алгоритма Хаффмана. Поскольку алгоритм работает рекурсивно, вызывая самого себя для последовательно сокращаемых алфавитов, будет естественно попытаться установить его оптимальность посредством индукции по размеру алфавита. Очевидно, он оптимален для всех двухбуквенных алфавитов (так как использует всего один бит на букву). Итак, предположим посредством индукции, что он оптимален для всех алфавитов размера k - 1, и рассмотрим входной экземпляр, состоящий из алфавита S размера k.

Напомним, как работает алгоритм для этого экземпляра: он объединяет две буквы с наименьшей частотой у*, z* ∈ S в одну букву ω, рекурсивно вызывает себя для сокращенного алфавита S' (в котором у* и z* заменены ω) и посредством индукции строит оптимальный префиксный код для S', представленный размеченным бинарным деревом T'. Полученный код расширяется в дерево Tдля S, для чего листья у* и z* присоединяются как дочерние узлы к узлу T с меткой ω.

Между метриками ABL(T) и ABL(T') существует тесная связь (первая — среднее количество битов, используемых для кодирования букв S, а вторая — среднее количество битов, используемых для кодирования букв S').

(4.32) ABL(T') = ABL(T) - f_ω.

Доказательство. Глубина каждой буквы х, за исключением у*, z*, одинакова в T и T'. Кроме того, каждая из глубин у* и z* в T на 1 больше глубины ω в T'. Используя это отношение, а также тот факт, что f_ω = f_y* + f_z*, получаем

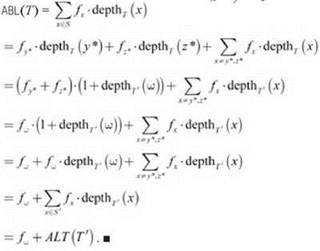
При помощи этой формулы теперь можно переходить к доказательству оптимальности.

(4.33) Код Хаффмана для заданного алфавита обеспечивает минимальное среднее количество битов на букву в любом префиксном коде.

Доказательство. Действуя от обратного, предположим, что построенное жадным алгоритмом дерево T не является оптимальным. Это означает, что существует размеченное бинарное дерево Z, такое что ABL(Z) < ABL(T); а согласно (4.31), существует такое дерево Z, в котором листья, представляющие у* и z* являются одноранговыми.

Теперь легко прийти к противоречию: если удалить из Z листья с метками у* и z* и пометить их бывшего родителя ю, мы получаем дерево Z', определяющее префиксный код S'. По тому же принципу, по которому дерево T получается из T', дерево Z получается из Z' посредством добавления листьев у* и z* под ω; следовательно, равенство из (4.32) также применимо к Z и Z': ABL(Z') = ABL(Z) - f_ω.

Но мы предполагали, что ABL(Z) < ABL(T ); вычитая f_ω из обеих сторон неравенства, получаем ABL(Z') < ABL(T'), что противоречит оптимальности T' как префиксного кода S'. ■

Реализация и время выполнения

Очевидно, что алгоритм Хаффмана может выполняться за полиномиальное время в зависимости от k — количества букв в алфавите. Рекурсивные вызовы алгоритма определяют серию k - 1 итераций по последовательно уменьшающимся алфавитам. Каждая итерация, кроме последней, состоит из простого нахождения двух букв с наименьшей частотой и слияния их в одну букву с суммарной частотой. Даже при простейшей реализации выявление букв с наименьшей частотой осуществляется за один проход по алфавиту с временем O(k), так что суммирование по k - 1 итерациям дает время O(k²).

Но в действительности алгоритм Хаффмана идеально подходит для использования приоритетной очереди. Вспомните, что приоритетная очередь используется для хранения множества из к элементов, каждый из которых имеет числовой ключ, и поддерживает операции вставки новых элементов и извлечения элемента с минимальным ключом. Таким образом, алфавит S может храниться в приоритетной очереди с использованием частоты каждой буквы в качестве ключа. При каждой итерации дважды извлекается минимальный элемент (две буквы с наименьшими частотами), после чего вставляется новая буква с ключом, равным сумме двух минимальных частот. В результате приоритетная очередь содержит представление алфавита, необходимое для следующей итерации.

С реализацией приоритетных очередей на базе кучи (см. главу 2) операции вставки и извлечения минимума выполняются за время O(log k); следовательно, каждая итерация, в которой выполняются всего три такие операции, выполняется за время O(log k). Суммирование по всем к итерациям дает общее время выполнения O(k log k).

Расширения

Структура оптимальных префиксных кодов, которые рассматривались в этом разделе, является фундаментальным результатом исследований в области сжатия данных. Но также важно понимать, что оптимальность никоим образом не означает, что обнаружен лучший способ сжатия данных в любых обстоятельствах.

Когда оптимального префиксного кода может оказаться недостаточно? Для начала представьте ситуацию с передачей черно-белых изображений: каждое изображение представляет собой массив из 1000 х 1000 пикселов и каждый пиксел принимает одно из двух значений (для черного или белого цвета). Также будем считать, что типичное изображение состоит почти полностью из белых пикселов: приблизительно 1000 из миллиона пикселов имеют черный цвет, а все остальные белые. При сжатии такого изображения весь метод префиксных кодов практически бесполезен: имеется текст из миллиона символов с двухбуквенным алфавитом {черный, белый}. Получается, что текст уже закодирован с использованием одного бита на букву — минимальной возможной длины в нашей системе кодирования.

Понятно, что такие изображения должны хорошо сжиматься. Интуитивно хотелось бы использовать “часть бита” для каждого из столь многочисленных белых пикселов, даже если каждый черный пиксел будет представляться несколькими битами. (В предельном случае отправка списка координат (x, y) всех черных пикселов будет работать эффективнее отправки изображения в виде текста с миллионом битов.) Проблема в том, чтобы определить схему кодирования с четко определенным понятием “части бита”. В этой области сжатия данных достигнуты определенные результаты; для подобных ситуаций разработан метод арифметического кодирования, а также ряд других способов.

Второй недостаток префиксных кодов в том виде, в каком они определяются здесь, заключается в том, что они не могут адаптироваться к изменениям в тексте. Снова рассмотрим простой пример. Допустим, мы хотим закодировать вывод программы, которая строит длинную последовательность букв из набора {a, b, с, d}. Также предположим, что в первой половине последовательности буквы а и b встречаются с равной частотой, а буквы c и d не встречаются вообще; во второй половине последовательности буквы c и d встречаются с равной частотой, а буквы а и b не встречаются вообще. В системе кодирования, разработанной в этом разделе, мы стремились организовать сжатие текста с четырехбуквенным алфавитом {a, b, c, d}, с равной частотой букв.

Но в этом примере в действительности частоты остаются стабильными в половине текста, а потом радикально изменяются. Например, следующая схема позволяет обойтись всего одним битом на букву, с небольшими затратами на хранение дополнительной информации:

♦ Начать с кодировки, в которой бит 0 представляет а, а бит 1 представляет b.

♦ На середине последовательности вставить инструкцию, которая сообщает: “Кодировка изменяется, с этого момента бит 0 представляет с, а бит 1 представляет d”.

♦ Использовать новую кодировку для оставшейся части последовательности.

Суть в том, что небольшие затраты на описание новой кодировки могут многократно окупиться, если они сокращают среднее количество битов на букву в длинном тексте. Методы, изменяющие кодировку внутри потока, называются адаптивными схемами сжатия. Для многих видов данных они приводят к существенным улучшениям по сравнению со статическим методом, который был рассмотрен выше.

Все эти аспекты дают представление о направлениях, в которых велась работа над сжатием данных. Как правило, существует компромисс между эффективностью метода сжатия и его вычислительной сложностью. В частности, многие усовершенствования только что описанных кодов Хаффмана приводят к соответствующему росту вычислительных затрат, необходимых для получения сжатой версии данных, их декодирования и восстановления исходного текста. Сейчас в области поиска баланса между ними идут активные исследования.