Упражнения с решениями - Урок 4 - Жадные алгоритмы

Упражнение с решением 1

Предположим, что трое ваших друзей, вдохновившись неоднократными просмотрами культового фильма “Ведьма из Блэр”, решили отправиться по Аппалачской тропе. Они хотят проходить как можно большее расстояние в дневное время, но по очевидным причинам не после наступления темноты. На карте обозначено множество хороших точек для разбивки лагеря. Чтобы выбрать место для остановки, они используют следующее правило: подходя к очередной возможной точке, они определяют, удастся ли им добраться до следующей точки до наступления темноты. Если время позволяет, то они продолжают идти, а если нет — останавливаются.

Несмотря на множество серьезных недостатков, эта система, по мнению ваших друзей, обладает одной полезной особенностью. “Раз мы идем только днем, — говорят они, — необходимое количество стоянок сводится к минимуму”.

Так ли это? Предлагаемая система выбора является жадным алгоритмом, и мы хотим определить, минимизирует ли он количество необходимых остановок.

Чтобы уточнить формулировку, сделаем несколько упрощающих предположений. Тропа будет моделироваться длинным отрезком прямой длины L; предполагается, что ваши друзья могут проходить d миль в день (независимо от рельефа, погоды и т. д.) Возможные точки остановок расположены на расстояниях x₁, x₂, ..., x_n от начала тропы. Также будем считать (очень великодушно), что ваши друзья никогда не ошибаются в оценке того, успеют ли они добраться до следующей точки остановки до наступления темноты.

Множество точек остановки считается действительным, если расстояние между каждой смежной парой не превышает d (для первой точки считается расстояние от начала тропы, а от последней — до конца тропы). Таким образом, действительность множества точек означает, что турист будет останавливаться только в этих точках и при этом доберется до конца тропы. Естественно, предполагается, что полное множество из n точек действительно, иначе пройти весь путь не удастся.

Теперь исходный вопрос можно сформулировать следующим образом. Является ли жадный алгоритм ваших друзей (ежедневный переход на максимально возможное расстояние) оптимальным в том смысле, что он находит действительное множество с минимально возможным размером?

Решение

Жадный алгоритм часто на первый взгляд выглядит правильным. Но прежде чем поддаваться его интуитивной привлекательности, полезно спросить себя: почему он может не работать? Какие скрытые проблемы в нем могут присутствовать?

Описанный алгоритм создает естественный вопрос: а не получится ли так, что более ранняя остановка позволит лучше синхронизироваться с возможностями выбора будущих дней? Но если над этим задуматься, начинаешь интересоваться, действительно ли это возможно. Может ли существовать альтернативное решение, которое намеренно отстает от жадного решения, а потом резко “набирает скорость” и обгоняет его? И как оно может обогнать, если жадное решение каждый день перемещается на максимально возможное расстояние?

Кажется, последний вопрос может стать основой для рассуждений, основанных на принципе “опережения” из раздела 4.1. Возможно, удастся показать, что если жадная стратегия идет впереди в любой конкретный день, никакое другое решение не сможет догнать и обогнать его в будущем.

Чтобы доказать, что этот алгоритм действительно оптимален, следует определить естественный смысл, по которому выбираемые им точки “идут впереди” любого другого действительного множества точек остановки. И хотя доказательство строится по той же схеме, что и доказательство из раздела 4.1, стоит отметить интересный контраст с задачей интервального планирования: в том случае доказывалось, что жадный алгоритм максимизирует нужную характеристику, а сейчас мы стремимся к минимизации некоторой характеристики.

Пусть — множество точек остановки, выбранное жадным алгоритмом. Действуя от противного, предположим, что существует меньшее действительное множество точек остановки такое что m < k.

Чтобы прийти к противоречию, сначала покажем, что точка остановки, достигаемая жадным алгоритмом в каждый день j, находится дальше точки остановки, достигаемой альтернативным решением, то есть

(4.40) Для всех j = 1, 2,..., m выполняется условие

Доказательство. Воспользуемся индукцией по j. Случай j = 1 очевиден из определения жадного алгоритма: в первый день туристы приходят максимально возможное расстояние, прежде чем остановиться. Теперь предположим, что j > 1, а предположение истинно для всех i < j. Тогда

так как S является действительным множеством точек остановки, и

так как по индукционной гипотезе. Объединяя эти два неравенства, получаем

Это означает, что у ваших друзей имеется возможность пройти весь путь от до за один день; а значит, точка в которой они в конечном счете остановятся, может находиться только дальше (Обратите внимание на сходство с соответствующим доказательством для задачи интервального планирования: здесь жадный алгоритм “идет впереди”, потому что на каждом шаге выбор, принимаемый альтернативным решением, является одним из его действительных вариантов.) ■

В частности, из (4.40) следует, что Теперь, если m < k, должно выполняться условие потому что в противном случае туристам не пришлось бы останавливаться в точке Объединяя эти два неравенства, можно сделать вывод, что но это противоречит предположению о том, что S является действительным множеством точек остановки.

Соответственно, предположение m < k было ложным, и мы доказали, что жадный алгоритм создает действительное множество точек остановки минимального возможного размера.

Упражнение с решением 2

Ваши друзья открывают компанию, занимающуюся компьютерной безопасностью, и им необходимо получить лицензии на n разных криптографических продуктов. Согласно действующим требованиям, они могут получать не более одной лицензии в месяц.

Каждая лицензия в настоящее время стоит $100, но со временем цена растет по экспоненциальному закону: в частности, лицензия j ежемесячно умножается на коэффициент r_j > 1 (где r_j — заданный параметр). Таким образом, если лицензия j приобретается через t месяцев, она будет стоить 100 ∙ r_jⁱ. Будем считать, что все скорости роста цены различны, то есть r_i ≠ r_j для i ≠ j(хотя все они начинаются с одной исходной цены $100).

Вопрос: если компания может покупать не более одной лицензии в месяц, в каком порядке следует совершать покупки, чтобы общая потраченная сумма была минимальной?

Приведите алгоритм, который получает n скоростей роста цены r₁, r₂, ..., r_n и вычисляет порядок покупки лицензий, чтобы общая сумма потраченных денег была минимальной. Время выполнения алгоритма должно быть полиномиальным по n.

Решение

Два естественных варианта выбора последовательности покупки — сортировка r в порядке убывания или возрастания. Сталкиваясь с подобными альтернативами, бывает полезно проработать маленький пример и посмотреть, не снимает ли он по крайней мере один из этих вариантов. Проверим вариант r₁ = 2, r₂ = 3 и r₃ = 4. Покупка лицензий по возрастанию обеспечивает общую стоимость

100(2 + 3² + 4³) = 7500,

тогда как при покупке в порядке убывания получается общая стоимость

100(4 + 3² + 2³) = 2100.

Вариант с упорядочением по возрастанию можно сразу отбросить. (С другой стороны, это не значит, что вариант с упорядочением по убыванию правилен, но по крайней мере мы исключили один из двух варинатов.)

Попробуем доказать, что сортировка r_i по убыванию действительно всегда приводит к оптимальному решению. Когда жадный алгоритм применяется в подобных задачах, в которых требуется разместить группу значений в оптимальном порядке, вы уже видели, что для доказательства правильности часто бывает эффективно воспользоваться методом замены.

Предположим, имеется оптимальное решение O, отличное от решения S. (Другими словами, S состоит из лицензий, отсортированных по убыванию). Значит, оптимальное решение O должно содержать инверсию, то есть должны существовать два смежных месяца t и t + 1, для которых скорость роста цены лицензии, купленной в месяце t (обозначим ее r_t), меньше, чем купленной в месяце t + 1 (обозначается r_t+1). Следовательно, r_t < r_t+1.

Утверждается, что, поменяв местами эти две покупки, можно строго улучшить оптимальное решение; это противоречит исходному предположению об оптимальности O. Следовательно, если нам удастся это доказать, мы успешно покажем, что алгоритм правилен.

Если поменять местами эти две покупки, остальные покупки будут иметь одинаковые цены. В О сумма, уплаченная за два месяца, задействованных в замене, будет равна другой стороны, если поменять эти две покупки местами, мы заплатим Поскольку константа 100 является общей для обоих выражений, нужно показать, что второй множитель больше первого. Итак, мы хотим показать, что

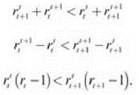
Но последнее неравенство истинно просто потому, что r_i > 1 для всех i, а значит, r_t < r_t+1.

На этом доказательство правильности можно считать завершенным. Время выполнения алгоритма равно O(n log n), поскольку сортировка занимает именно такое время, а остальные операции (вывод) выполняются за линейное время. Итак, общее время выполнения равно O(n log n).

Примечание: интересно, что даже при небольшом изменении вопроса ситуация существенно усложняется. Предположим, вместо покупки лицензий с возрастающей ценой вы пытаетесь продавать оборудование, цена которого последовательно снижается. Цена элемента У снижается с коэффициентом r_i < 1 в месяц, начиная с $100, так что при продаже его через t месяцев вы получите (Иначе говоря, скорость роста теперь не больше, а меньше 1.) Если в месяц продается только один вид оборудования, в каком оптимальном порядке их следует продавать? Как выясняется, существуют ситуации, в которых оптимальное решение не упорядочивает коэффициенты по возрастанию или убыванию (как с входными данными ).

Упражнение с решением 3

Предположим, имеется связный граф G; будем считать, что стоимости всех ребер различны. Граф G содержит n вершин и m ребер. Задано конкретное ребро e графа G. Предложите алгоритм со временем выполнения O(m + n), который будет решать, содержится ли e в минимальном остовном дереве G.

Решение

Мы знаем, что принадлежность ребра e минимальному остовному дереву проверяется по двум правилам: свойство сечения (4.17) утверждает, что e присутствует в минимальном остовном дереве, если это ребро с наименьшей стоимостью, переходящее из некоторого множества S в дополнение V - S; а свойство цикла (4.20) утверждает, что е не включается ни в какое минимальное остовное дерево, если это ребро с наибольшей стоимостью в некотором цикле C. Удастся ли нам использовать эти два правила как часть алгоритма, который решает задачу за линейное время?

Оба свойства фактически определяют, в каких отношениях e находится с множеством ребер, обладающих меньшей стоимостью, чем у е. Свойство сечения можно рассматривать как вопрос: существует ли такое множество S ⊆ V, чтобы для перехода из S в V - S без использования е пришлось бы использовать ребро с большей стоимостью, чем у е? И если взглянуть на цикл C в контексте свойства цикла, “длинный путь” по C (в обход e) может рассматриваться как альтернативный маршрут между конечными точками e, использующими только ребра с меньшей стоимостью.

Объединяя эти два наблюдения, мы приходим к следующему утверждению.

(4.41) Ребро е = (v, w) не принадлежит минимальному остовному дереву графа G в том, и только в том случае, если v и w можно соединить путем, состоящим исключительно из ребер с меньшей стоимостью, чем у е.

Доказательство. Сначала предположим, что P — путь v-w, состоящий исключительно из ребер с меньшей стоимостью, чем у е. Если добавить е в P, мы получим цикл, для которого е является самым “дорогостоящим” ребром. Следовательно, по свойству цикла е не принадлежит минимальному остовному дереву G.

С другой стороны, предположим, что v и w невозможно соединить путем, состоящим исключительно из ребер со стоимостью меньшей, чем у е. Определим множество S, для которого е является ребром с наименьшей стоимостью, один конец которого находится в S, а другой в V - S; если это возможно, то из свойства сечения следует, что е принадлежит каждому минимальному остовному дереву. Наше множество S будет представлять собой множество всех узлов, к которым можно перейти из v по пути, состоящему только из ребер со стоимостью меньшей, чем у е. Согласно нашему предположению, w ∈ V - S. Кроме того, по определению S не может существовать ребро f = (x, у) со стоимостью меньшей, чем у е, для которого один конец x принадлежит S, а другой конец у — V - S. В самом деле, если бы такое ребро f существовало, то раз к узлу x можно перейти из v по ребрам только с меньшей стоимостью, чем у е, узел у также был бы достижим. Следовательно, е — ребро с наименьшей стоимостью, один конец которого принадлежит S, а другой — V - S, как и требовалось. Доказательство закончено. ■

С учетом этого факта наш алгоритм выглядит так. Мы строим граф G', удаляя из G все ребра с весом, превышающим с_е (а также само ребро е). Затем при помощи одного из алгоритмов связности из главы 3 он определяет, существует ли путь от v к w в G'. Согласно (4.41), е принадлежит минимальному остовному дереву в том, и только в том случае, если такой путь не существует.

Время выполнения этого алгоритма включает O(m + n) для построения G' и O(m + n) для проверки пути от v к w.

Упражнения

1. Решите, истинно или ложно следующее утверждение. Если оно истинно, приведите краткое объяснение, а если ложно — контрпример.

Пусть G — произвольный связный ненаправленный граф с различающимися стоимостями c(e) всех ребер e. Предположим, e* — ребро с минимальной стоимостью в G, то есть c(e*) < c(e) для каждого ребра е ≠ e*. Тогда существует минимальное остовное дерево T графа G, содержащее ребро e*.

2. Решите, истинно или ложно каждое из следующих двух утверждений. Если утверждение истинно, приведите краткое объяснение, а если ложно — контрпример.

(a) Предположим, имеется экземпляр задачи нахождения минимального остовного дерева для графа G, все стоимости ребер которого положительны и различны. Пусть Т — минимальное остовное дерево для этого экземпляра. Стоимость каждого ребра с_е заменяется его квадратом с_e²; так образуется новый экземпляр задачи с тем же графом, но другими стоимостями. Истинно или ложно? Дерево T должно остаться минимальным остовным деревом для нового экземпляра задачи.

(b) Предположим, имеется экземпляр задачи нахождения кратчайшего пути s-t в направленном графе G. Все стоимости ребер положительны и различны. Пусть Р — путь s-t для этого экземпляра с минимальной стоимостью. Стоимость каждого ребра с_е заменяется его квадратом с_e²; так образуется новый экземпляр задачи с тем же графом, но другими стоимостями.

Истинно или ложно? Путь P должен остаться путем s-t c минимальной стоимостью для нового экземпляра задачи.

3. Вы консультируете транспортную компанию, которая перевозит грузы между Нью-Йорком и Бостоном. Объем перевозок достаточно велик, чтобы ежедневно между двумя городами отправлялось несколько грузовиков. У каждого грузовика имеется предельный вес перевозимых грузов W. Грузы прибывают на склад в Нью-Йорке один за другим, каждый пакет i имеет вес w_i. Склад невелик, поэтому в любой момент времени на нем может находиться только один грузовик. По действующим в компании правилам грузы отправляются в порядке их поступления, чтобы покупатели не сердились, если груз, отправленный позднее их груза, доберется до Бостона раньше. Сейчас в компании используется простой жадный алгоритм упаковки: грузы упаковываются в порядке поступления, а если следующий груз не помещается, то грузовик отправляется без него.

Но владельцы компании подозревают, что они используют слишком много грузовиков, и хотят повысить эффективность. Нельзя ли сократить количество машин, отправляя незаполненный грузовик, чтобы следующие грузовики заполнялись более эффективно?

Докажите, что для заданного набора грузов с заданными весами жадный алгоритм, используемый в настоящее время, действительно минимизирует количество используемых грузовиков. Доказательство должно строиться по тому же образцу, что и приведенное выше доказательство для задачи интервального планирования: оптимальность жадного алгоритма устанавливается определением метрики, в соответствии с которой он “опережает” все остальные решения.

4. Ваши друзья занялись расширяющейся областью анализа временных рядов. Целью анализа является поиск закономерностей в последовательностях событий, происходящих во времени. Одним из источников таких данных с естественным упорядочением по времени могут служить покупки на биржах (что и когда покупается). Ваши друзья хотят иметь эффективный механизм обнаружения некоторых “закономерностей” в заданной последовательности S таких событий: например, они хотят знать, происходят ли в последовательности S четыре события

в такой очередности (но не обязательно подряд).

Они начинают с набора всех возможных событий (например, возможных транзакций) и последовательности S из n таких событий. Заданное событие может встречаться в S несколько раз (например, акции Yahoo могут покупаться многократно в одной последовательности S). Последовательность S' называется подпоследовательностью S, если из S возможно удалить некоторые события так, чтобы оставшиеся события (с соблюдением порядка) были равны последовательности S'. Так, приведенная последовательность из четырех событий является подпоследовательностью для последовательности

Ваши друзья хотят вводить короткие последовательности и быстро узнавать, являются ли они подпоследовательностями S. Поставлена следующая задача: предложите алгоритм, который получает две последовательности событий — S' длины m и S длины n (в обеих последовательностях события могут повторяться) и за время O(m + n) решает, является ли S' подпоследовательностью S.

5. Представьте длинную, спокойную проселочную дорогу, на которой редко встречаются отдельные дома. (Будем считать, что дорога представляет собой отрезок прямой с двумя концами, восточным и западным.) Также предположим, что несмотря на пасторальную обстановку, жители этих домов активно пользуются мобильными телефонами. Требуется разместить базовые станции сотовой связи вдоль дороги так, чтобы любой дом находился на расстоянии не более четырех миль от одной из базовых станций.

Предложите эффективный алгоритм для достижения этой цели с минимальным количеством базовых станций.

6. Ваш друг работает в детском лагере и отвечает за проведение мероприятий в группе подростков. В его планы входит проведение мини-триатлона: каждый участник должен проплыть 20 дорожек в бассейне, проехать на велосипеде 10 миль, а потом пробежать 3 мили. Участники будут выходить на дистанцию поочередно, по следующему правилу: в любой момент времени бассейн будет использоваться только одним участником. Другими словами, первый участник проплывает 20 дорожек, выходит и садится на велосипед. Как только он покидает бассейн, второй участник начинает проплывать свои 20 дорожек; когда он выходит из бассейна, заплыв начинает третий участник... и т. д.

У каждого участника имеется прогнозируемое время плавания (время, за которое он должен проплыть 20 дорожек), прогнозируемое время проезда (время, за которое он должен проехать 10 миль) и прогнозируемое время бега (время, за которое он пробежит 3 мили). Ваш друг хочет спланировать расписание триатлона: порядок, в котором участники будут выходить на дистанцию. Завершающим временем расписания будет называться самое меньшее время, за которое все участники пройдут все три стадии триатлона, при условии, что они точно выдержат спрогнозированное время во всех трех стадиях (еще раз: участники могут ехать на велосипеде и бежать одновременно, но в бассейне в любой момент времени может находиться только один человек). Как выглядит оптимальный порядок выхода участников, чтобы соревнования закончились как можно раньше? А точнее, предложите эффективный алгоритм, который строит расписание с минимальным завершающим временем.

7. Невероятно популярная испаноязычная поисковая система Goog проводит огромный объем вычислений при каждом пересчете индекса. К счастью, в распоряжении компании имеется один суперкомпьютер с практически неограниченным запасом мощных рабочих станций.

Вычисления разбиты на n заданий J₁, J₂, ..., J_n, которые могут выполняться полностью независимо друг от друга. Каждое задание состоит из двух фаз: сначала оно проходит предварительную обработку на суперкомпьютере, а затем завершается на одной из рабочих станций. Допустим, обработка задания J_i требует р_i секунд на суперкомпьютере, а затем f_i секунд на рабочей станции. На площадке доступны как минимум n рабочих станций, поэтому завершающая фаза обработки всех заданий может проходить параллельно — все задания будут выполняться одновременно. Однако суперкомпьютер может работать только с одним заданием, поэтому администратор должен определить порядок передачи заданий суперкомпьютеру. Как только первое задание в этом порядке будет обработано на суперкомпьютере, оно передается на рабочую станцию для завершения; после обработки на суперкомпьютере второе задание передается на рабочую станцию независимо от того, завершилось первое задание или нет (так как рабочие станции работают параллельно), и т. д.

Допустим, расписание представляет собой упорядоченный список заданий для суперкомпьютера, а время завершения расписания определяется самым ранним временем завершения всех заданий на рабочих станциях. Очень важно свести к минимуму эту характеристику, так как она определяет, насколько быстро El Goog сможет построить новый индекс.

Предложите алгоритм с полиномиальным временем, который находит расписание с минимальным временем завершения.

8. Имеется связный граф G, стоимости всех ребер которого различны. Докажите, что в G существует уникальное минимальное остовное дерево.

9. Одна из практических целей для задачи нахождения минимального остовного дерева — построение остовной сети для множества узлов с минимальной общей стоимостью. Однако сейчас нас интересует другой тип целей: проектирование остовной сети, в которой максимальная стоимость ребра настолько низка, насколько это возможно.

Говоря конкретнее, пусть G = (V, E) — связный граф с n вершинами, m ребрами и положительными стоимостями ребер (предполагается, что все стоимости различны). Пусть T = (V, E') — остовное дерево G; критическим ребром дерева T будет называться ребро из T с наибольшей стоимостью.

Остовное дерево T графа G называется минимально-критическим остовным деревом, если не существует остовного дерева T' графа G с меньшей стоимостью критичного ребра.

(a) Является ли каждое минимально-критичное дерево графа G минимальным остовным деревом G? Докажите или приведите контрпример.

(b) Является ли каждое минимальное остовное дерево графа G минимальнокритичным деревом графа G? Докажите или приведите контрпример.

10. Пусть G = (V, E) — (ненаправленный) граф со стоимостями с_е ≥ 0 ребер e ∈ E. Допустим, вам известно минимальное остовное дерево T для G. Предположим, что в G добавляется новое ребро, соединяющее два узла v, w ∈ V со стоимостью с.

(a) Предложите эффективный алгоритм проверки того, остается ли T остовным деревом минимальной стоимости при добавлении нового ребра в G (но не в дерево T). Алгоритм должен выполняться за время O(|E|). Удастся ли вам заставить его выполняться за время O(|V|)? Отметьте все предположения, которые вам пришлось сделать относительно структуры данных, используемой для представления дерева T и графа G.

(b) Допустим, T уже не является минимальным остовным деревом. Предложите алгоритм с линейным временем (O(|E|)) для замены T новым минимальным остовным деревом.

11. Предположим, имеется связный граф G = (V, E), ребро e которого имело стоимость с_e. В предыдущей задаче было показано, что при различных стоимостях ребер G содержит уникальное минимальное остовное дерево. Но если в графе имеются ребра с одинаковой стоимостью, G может содержать несколько минимальных остовных деревьев. Вопрос: можно ли заставить алгоритм Крускала найти все минимальные остовные деревья графа G?

Вспомните, что алгоритм Крускала сортирует ребра в порядке увеличения стоимости, а затем жадно обрабатывает ребра одно за другим, добавляя ребро e при условии, что оно не приводит к образованию цикла. Когда некоторые ребра имеют одинаковую стоимость, выражение “в порядке увеличения стоимости” необходимо задать более тщательно: упорядочение ребер называется действительным, если соответствующая последовательность стоимостей ребер не уменьшается. Действительным выполнением алгоритма Крускала будет называться выполнение, начинающее с действительного упорядочения ребер G.

Для любого графа G и любого минимального остовного дерева T графа G существует ли действительное выполнение алгоритма Крускала для G, которое выдает T как результат? Приведите доказательство или контрпример.

12. Предположим, имеется n видеопотоков, которые необходимо передать один за другим по каналу связи. Поток i состоит из b_i битов, которые должны передаваться с постоянной скоростью за период t_i секунд. Два потока не могут передаваться одновременно, поэтому необходимо составить расписание потоков, то есть порядок их отправки. Какой бы порядок ни был выбран, задержек между концом одного и началом следующего потока быть не должно. Предположим, расписание начинается во время 0 (а следовательно, завершается во время независимо от выбранного порядка). Предполагается, что все значения b_i и t_i — положительные целые числа.

Владелец канала не хочет, чтобы один пользователь создавал слишком большую нагрузку на канал, поэтому он устанавливает следующее ограничение с фиксированным параметром r:

(*) Для каждого натурального числа t > 0 общее количество битов, передаваемых за интервал времени от 0 до t, не может превышать r_i. Обратите внимание: ограничения устанавливаются только для интервалов, начинающихся с 0 (но не для любой другой начальной точки).

Расписание называется действительным, если оно удовлетворяет ограничению (*), установленному для канала.

Задача. Для заданного множества из n потоков, каждый из которых задается количеством битов b_i и продолжительностью t_i, а также для параметра канала r определите, существует ли действительное расписание.

Пример. Предположим, имеются n = 3 потока с параметрами (b₁, t₁) = (2000, 1), (b₂, t₂) = (6000, 2), (b₃, t₃) = (2000, 1), а параметр канала r = 5000. В этом случае расписание, передающее потоки в порядке 1, 2, 3, будет действительным, так как ограничение (*) соблюдается:

t = 1: весь первый поток отправлен, 2000 < 5000 ∙ 1

t = 2: отправлена половина второго потока, 2000 + 3000 < 5000 ∙ 2

Аналогичные вычисления проводятся для t = 3 и t = 4.

(a) Рассмотрим следующее утверждение:

Действительное расписание существует в том, и только в том случае, если каждый поток i удовлетворяет условию b_i ≤ rt_i.

Решите, истинно или ложно это утверждение. Предоставьте доказательство или контрпример.

(b) Предложите алгоритм, который получает множество из n потоков, каждый из которых задается количеством битов b_i и продолжительностью t_i, а также параметр канала r и определяет, существует ли для них действительное расписание. Время выполнения алгоритма должно быть полиномиальным по n.

13. Небольшая фирма — скажем, копировальный центр с одним большим копировальным аппаратом — сталкивается с проблемой планирования. Каждое утро она получает множество заказов от клиентов. Заказы должны быть выполнены на единственном аппарате в порядке, который устроит большинство клиентов. На выполнение заказа клиента i требуется время t_i. Пусть при заданном расписании (то есть порядке заказов) время завершения заказа i обозначается C. Например, если задание j должно быть выполнено первым, то C_j = t_j; а если задание j выполняется сразу же после задания i, то C_j = C_i + t_j. Каждому клиенту i также назначается вес w_i, представляющий его важность для фирмы. Настроение клиента i зависит от времени завершения его заказа. Таким образом, фирма стремится упорядочить заказы так, чтобы свести к минимуму взвешенную сумму времен завершения,

Предложите эффективный алгоритм для решения этой задачи. Алгоритм получает множество из n заказов с временем обработки t_i и весом w_i для каждого заказа. Требуется упорядочить заказы так, чтобы минимизировать взвешенную сумму времен завершения

Пример. Предположим, получены два заказа: первый с временем t₁ = 1 и весом w₁ = 10, и второй с временем t₂ = 3 и весом w₂ = 2. Если заказ 1 будет выполнен первым, то взвешенное время завершения составит 10 ∙ 1 + 2 ∙ 4 = 18, а если начать со второго заказа, то взвешенное время увеличится до 10 ∙ 4 + 2 ∙ 3 = 46.

14. Вы работаете с группой консультантов в области безопасности, которые наблюдают за работой большой компьютерной системы. Особый интерес вызывают процессы с пометкой “системный”. Для каждого такого процесса задано начальное и конечное время; в промежутке между этими моментами процесс непрерывно работает; у консультантов имеется список начального и конечного времени для всех системных процессов, запланированных на сегодняшний день.

Консультанты написали программу status_check, которая выполняется несколько секунд и сохраняет различную информацию о системных процессах, выполняемых в системе в настоящее время. (В нашей модели каждый вызов status_check относится только к одному конкретному моменту времени.) Консультанты хотели бы запускать программу status_check как можно меньше раз за день, но достаточно для того, чтобы на протяжении выполнения каждого системного процесса P программа была запущена хотя бы один раз.

(а) Предложите эффективный алгоритм, который получает начальное и конечное время для всех системных процессов и находит минимальное множество временных точек для вызова status_check, с которым программа будет вызвана хотя бы один раз на протяжении работы каждого системного процесса P.

(b) Пока вы работали над алгоритмом, консультанты тоже пытались найти подход к решению задачи. “Допустим, нам удастся найти множество из к системных процессов, обладающих тем свойством, что никакие из них никогда не выполняются одновременно. Тогда, очевидно, алгоритм должен вызвать status_check минимум к раз; каждый отдельный вызов status_check сможет обработать только один из таких процессов”.

Конечно, это правильно, и в дальнейшем обсуждении возник вопрос: а не действует ли более сильное правило, своего рода обратное приведенному? Предположим, k* — наибольшее значение k, позволяющее найти множество из k системных процессов, никакие два из которых никогда не выполняются одновременно. Значит ли это, что должно существовать множество из k* моментов времени для запуска status_check, чтобы хотя бы один вызов случился во время выполнения каждого системного процесса? (Другими словами, не является ли аргумент из предыдущего абзаца единственной причиной, по которой приходится много раз вызывать status_check?) Решите, истинно или ложно это утверждение, и приведите доказательство или контрпример.

15. К вам обращается менеджер крупного студенческого объединения. Она руководит группой из n студентов, каждый из которых по графику должен отработать одну смену за неделю. Со сменами связаны различные виды работ (помощь в доставке пакетов, перезагрузка зависших информационных терминалов и т. д.), но мы можем рассматривать каждую смену как один непрерывный интервал времени. Несколько смен могут проходить одновременно.

Менеджер хочет выбрать подмножество из этих n студентов и сформировать наблюдательный комитет, с которым будет проводить встречи раз в неделю. Комитет будет считаться полным, если у каждого студента, не входящего в комитет, смена перекрывается (по крайней мере частично) со сменой студента, входящего в комитет. Таким образом, качество работы каждого студента будет видно по крайней мере одному участнику комитета.

Приведите эффективный алгоритм, который получает расписание из n смен и выдает состав полного наблюдательного комитета с минимальным количеством участников.

Пример. Предположим, n = 3 и смены проводятся в следующее время: понедельник 16:00 — понедельник 20:00 понедельник 18:00 — понедельник 22:00 понедельник 21:00 — понедельник 23:00 В этом случае наименьший полный наблюдательный комитет будет состоять только из второго студента, потому что вторая смена перекрывается как с первой, так и с третьей.

16. Консультанты по вопросам финансовой безопасности в настоящее время работают с клиентом, исследующим потенциальную схему отмывания денег. Проведенные исследования показали, что за последнее время состоялось n сомнительных операций, каждая из которых была связана с переводом денег на некий счет. К сожалению, отрывочный характер доказательств означает, что исследователям неизвестен сам счет, суммы переводов и точное время проведения операций. Известна лишь приблизительная временная метка каждой операции; из доказательств следует, что операция i состоялась во время t_i ± е_i с некоторой “погрешностью” е_i. (Иначе говоря, операция состоялась где-то в интервале от t_i – е_i до t_i + е_i). Не забывайте, что у разных операций могут быть разные погрешности.

Недавно был обнаружен подозрительный банковский счет, который, как предполагается, мог быть использован в преступлении. За последнее время со счетом выполнялись n операций, происходивших во время x₁, x₂, ..., x_n. Чтобы узнать, тот это счет или нет, нужно связать каждое из n событий с одной из n сомнительных операций так, чтобы если событие x_. связывается с сомнительной операцией t_j, то выполнялось условие │t_j – x_i│ < е_j. (Иначе говоря, клиент хочет знать, можно ли связать события с сомнительными операциями так, чтобы временные расхождения находились в пределах разумной погрешности; задача усложняется тем, что заранее неизвестно, какое событие с какой погрешностью должно связываться.)

Предложите эффективный алгоритм, который получает данные и решает, существует ли такая ассоциация. Если возможно, алгоритм должен выполняться за время не более O(n²).

17. Рассмотрим следующую вариацию на тему задачи интервального планирования. Имеется компьютер, который может работать ежедневно по 24 часа в сутки. Пользователи подают заявки на выполнение ежедневных заданий на компьютере. У каждого задания имеется начальное и конечное время; если задание принято на выполнение, оно выполняется каждый день в период между начальным и конечным временем. (Обратите внимание: задания могут начинаться до полуночи и завершаться после полуночи; из-за этого ситуация отличается от той, какую мы видели в задаче интервального планирования.) Получив список из n таких заданий, нужно принять как можно больше заданий (независимо от их длины) с учетом ограничения, согласно которому в любой момент времени на компьютере может выполняться только одно задание. Предложите алгоритм решения этой задачи с временем, полиномиальным по n. Для простоты можно считать, что не существует заданий с одинаковым начальным и конечным временем.

Пример. Получены следующие четыре задания, заданных парами (начало, конец):

(18:00, 6:00), (21:00, 4:00), (3:00, 14:00), (13:00, 19:00)

В оптимальном варианте выбираются два задания (21:00, 4:00) и (13:00, 19:00), которые могут быть запланированы без перекрытия по времени.

18. Ваши друзья собрались в зимний поход к небольшому городку возле канадской границы. Они проанализировали все варианты перемещений и построили направленный граф, узлы которого представляют промежуточные пункты, а ребра — соединяющие их дороги.

Также известно, что из-за плохой погоды некоторые дороги в этой местности зимой заметает и перемещение по ним может существенно замедлиться. К счастью, имеется отличный сайт с точными прогнозами скорости перемещения по дорогам; однако эта скорость зависит от времени года. Точнее, сайт отвечает на запросы следующего вида: имеется ребро e = (v, w), соединяющее два пункта v и w; для заданного начального времени t для пункта v сайт возвращает значение f_e(t) прогнозируемое время прибытия в w. Сайт гарантирует, что f_e(t) ≥ t для всех ребер e и моментов времени t (обратные перемещения во времени невозможны), а f_e(t) является монотонно возрастающей функцией t (то есть отправившись в путь позднее, вы не приедете раньше). В остальном функции _fe(t) могут быть произвольными. Например, в местах, в которых скорость перемещения не зависит от времени года, f_e(t) = t + l_e, где l_e — время, необходимое для перемещения от начала ребра e к его концу.

Ваши друзья хотят использовать сайт для определения самого быстрого способа перемещения по направленному графу от начальной точки до места назначения. (Предполагается, что они отправляются во время 0, а все прогнозы сайта полностью верны.) Предложите алгоритм с полиномиальным временем для решения этой задачи; отправка одного запроса на сайт (с заданным ребром e и временем t) рассматривается как отдельный шаг вычислений.

19. Группа планирования сети из коммуникационной компании CluNet столкнулась со следующей задачей. Имеется связный граф G = (V, E); узлы графа представляют точки, с которыми требуется организовать обмен данными. Каждое ребро e представляет канал связи с заданной пропускной способностью b_e.

Для каждой пары узлов u, v ∈ V требуется выбрать один путь P из u в v, по которому эта пара будет обмениваться данными. Критической пропускной способностьюb(P) этого пути P называется минимальная пропускная способность всех входящих в него ребер; иначе говоря, b(P) = min_e∈pb_e. Лучшей достижимой пропускной способностью для пары u, v в графе G называется максимум значения b(P) по всем путям P для пар u-v в графе G.

С какого-то момента отслеживать пути для всех пар узлов в сети становится слишком сложно, и один из проектировщиков сети выступает со смелым предложением: нельзя ли найти остовное дерево T для G, в котором для каждой пары узлов и, v уникальный путь u-v в дереве будет обеспечивать лучшую достижимую пропускную способность для маршрута u-v в G? (Иначе говоря, хотя путь u-v может выбираться по всему графу, улучшить результат по сравнению с путем u-v в T все равно не удастся.)

В CluNet эта идея подверглась дружной критике, и у этого скептицизма имеется естественная причина: пути, которые будут использоваться для обеспечения пропускной способности между двумя узлами, могут сильно отличаться. С чего бы полагать, что одно дерево одновременно решит все проблемы? Но после нескольких неудачных попыток опровергнуть идею люди начинают подозревать, что это все же возможно.

Докажите, что такое дерево существует, и предложите эффективный алгоритм его построения. Иначе говоря, предложите алгоритм построения остовного дерева T, в котором для каждой пары u, v ∈ V пропускная способность пути u-v в T равна лучшей достижимой пропускной способности для пары u, v в графе G.

20. Ежегодно осенью в отдаленной горной местности собирается группа представителей дорожных служб, которая выбирает, какие дороги следует постоянно расчищать предстоящей зимой. В округе n городов, а дорожная сеть может рассматриваться как (связный) граф (V, E) для этого множества городов; каждое ребро представляет дорогу, соединяющую два города. Зимой людей, живущих в горах, беспокоит не столько длина дороги, сколько высота — именно она начинает определять сложность поездки.

Каждая дорога (каждое ребро е в графе) помечается числом а_е, определяющим высоту самой высокой точки дороги. Будем считать, что в графе нет двух ребер с одинаковым значением а_е. Высота пути P в графе определяется максимальным значением а_е для всех ребер е, входящих в P. Наконец, путь между городами i и j считается оптимальным, если он обеспечивает минимально возможную высоту по всем путям от i до j.

Представители дорожных служб собираются выбрать множество E' ⊆ E дорог, которые будут расчищаться зимой; снег на остальных дорогах убираться не будет, и они станут недоступными для путешественников. Все согласны с тем, что какое бы подмножество дорог E' ни было выбрано, оно должно обладать тем свойством, что (V, E') является связным подграфом; и что еще важнее, для каждой пары городов i и j высота оптимального пути в (V, E') не должна быть больше, чем в полном графе G = (V, E). Связный подграф (V, E'), обладающий этим свойством, будет называться связным подграфом с минимальной высотой. Но если это ключевое свойство соблюдается, дорожные службы хотели бы свести к минимуму количество расчищаемых дорог. И вот однажды они выдвигают следующую гипотезу:

Минимальное остовное дерево графа G с весами ребер а_е является связным графом с минимальной высотой.

(В одной из предшествующих задач утверждалось, что при различающихся весах ребер существует уникальное минимальное остовное дерево. Следовательно, благодаря предположению о том, что все значения а_е различны, можно говорить о минимальном остовном дереве.)

Изначально эта гипотеза выглядит неочевидной, поскольку минимальное остовное дерево стремится минимизировать сумму значений а_е, а цель минимизации высоты кажется чем-то совершенно иным. Однако при отсутствии опровержений выдвигается еще более смелая вторая гипотеза:

Подграф (V, E') является связным подграфом с минимальной высотой в том, и только в том случае, если он содержит ребра минимального остовного дерева. Обратите внимание: из второй гипотезы немедленно следует первая, так как минимальное остовное дерево содержит свои ребра.

Вопросы:

(a) Является ли первая гипотеза истинной для всех вариантов выбора G и различающихся высот а_e? Представьте доказательство или контрпример с объяснением.

(b) Является ли вторая гипотеза истинной для всех вариантов выбора G и различающихся высот а_e? Представьте доказательство или контрпример с объяснением.

21. Будем называть граф G = (V, E) квазидеревом, если он является связным и содержит не более n + 8 ребер, где n = |V|. Предложите алгоритм с временем выполнения O(n), который получает квазидерево G со стоимостями всех ребер и возвращает минимальное остовное дерево графа G. Считайте, что все стоимости ребер различны.

22. Рассмотрим задачу нахождения минимального остовного дерева для ненаправленного графа G = (V, E) со стоимостью c_e ≥ 0 каждого ребра; при этом стоимости ребер могут совпадать. Если граф может содержать ребра с одинаковой стоимостью, то и решений с минимальной стоимостью может быть несколько. Предположим, имеется остовное дерево T ⊆ E с гарантией того, что каждое ребро e ∈ T принадлежит некоторому минимальному остовному дереву графа G. Можно ли заключить, что T является минимальным остовным деревом G? Представьте доказательство или контрпример с объяснением.

23. Вспомните задачу вычисления ориентированного дерева с минимальной стоимостью в направленном графе G = (V, E) со стоимостями ребер c_e > 0. Здесь мы рассмотрим случай, в котором Gявляется направленным ациклическим графом (DAG), то есть не содержит направленных циклов.

Как и в случае с направленными графами вообще, разных решений с минимальной стоимостью может быть много. Допустим, имеется направленный ациклический граф G = (V, E) и ориентированное дерево A ⊆ E с гарантией того, что каждое ребро e ∈ A принадлежит некоторому ориентированному дереву с минимальной стоимостью в G. Можно ли сделать вывод, что Aявляется ориентированным деревом с минимальной стоимостью в G? Представьте доказательство или контрпример с объяснением.

24. Цепи синхронизации — один из важнейших компонентов больших интегральных схем. Ниже представлена простая модель такой цепи. Возьмем полное сбалансированное бинарное дерево с n листьями, где n — степень 2. С каждым ребром e дерева связана длина I, которая является положительным числом. Расстояние от корня до заданного листа вычисляется суммированием длин всех ребер пути от корня к листу.

Корень генерирует синхросигнал, который распространяется по ребрам к листьям. Будем считать, что время, необходимое сигналу для перехода к заданному листу, пропорционально расстоянию от корня до листа.

Если расстояния от листьев до корня различны, то сигнал дойдет до листьев в разное время, и это создаст большие проблемы. Мы хотим, чтобы листья были полностью синхронизированы и получали сигнал одновременно. Для этого необходимо увеличить длины некоторых ребер, чтобы все пути от корня до листьев имели одинаковую длину (уменьшить длины ребер нельзя). Если эта задача будет решена, то дерево (с новыми длинами ребер) имеет нулевой сдвиг. Наша цель — обеспечить нулевой сдвиг так, чтобы сумма длин всех ребер оставалась минимальной.

Предложите алгоритм, увеличивающий длину некоторых ребер так, чтобы полученное дерево имело нулевой сдвиг, а общая длина ребер была минимально возможной.

Пример. Рассмотрим дерево на рис. 4.20, на котором буквами обозначены узлы, а числами — длины ребер.

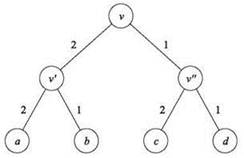
Рис. 4.20. Задача нулевого сдвига из упражнения 23

Уникальное оптимальное решение для этой задачи — взять три ребра длины 1 и увеличить каждую из этих длин до 2. Полученное дерево имеет нулевой сдвиг, а сумма длин ребер равна 12 (минимальная из возможных).

25. Имеется множество точек P = {p₁, p₂, ..., p_n} и функция расстояния d для множества P; d — функция для пары точек в P, обладающая тем свойством, что d(p_i, p_j) = d(p_j, p_i) > 0, если i ≠ j, а d(p_i, p_i) = 0 для каждого i.

Определим иерархическую метрику для P как произвольную функцию расстояния τ, которая строится следующим образом: строим корневое дерево T с n листьями и назначаем каждому узлу vдерева T (как листьям, так и дочерним узлам) высоту h_v. Высоты должны удовлетворять следующим условиям: h(v) = 0 для каждого листа v, и если и является родителем v в T, то h(u) ≥ h(v). Каждая точка из P ставится в соответствие отдельному листу T. Теперь для каждой пары точек p_i и p_j определяется расстояние между ними т(p_i, p_j): мы находим наименьшего общего предка v в T для листьев, содержащих p_i и p_j, и определяем т(p_i, p_j) = h_v.

Иерархическая метрика т называется согласованной с функцией расстояния d, если для всех пар i, j выполняется условие т(p_i, p_j) ≤ d(p_i, p_j).

Предложите алгоритм с полиномиальным временем, который получает функцию расстояния d и выдает иерархическую метрику т со следующими свойствами:

(i) метрика т согласована с d, и

(ii) если т' — любая другая иерархическая метрика, согласованная с d, то т'(p_i, p_j) ≤ т(p_i, p_j) для каждой пары точек p_i и p_j.

26. Одна из первых задач, рассматриваемых в курсе математического анализа, — задача минимизации дифференцируемой функции (например, y = ax² + bx + c для a > 0). С другой стороны, задача нахождения минимального остовного дерева относится к совершенно иной разновидности задач минимизации: количество вариантов для достижения минимума ограничеуно, но вычисления должны проводиться без перебора этого (огромного) конечного числа возможностей.

Что произойдет, если свести воедино эти две разновидности минимизации? Ниже приведен пример задачи такого рода. Допустим, имеется связный граф G = (V, E); переменная стоимостькаждого ребра изменяется во времени в соответствии с функцией f_e: R→R. Таким образом, в момент времени t ребро имеет стоимость f_e(t). Предполагается, что все функции принимают положительные значения на всем интервале значений. Заметьте, что множество ребер, образующих минимальное остовное дерево графа G, может изменяться со временем. Конечно, стоимость минимального остовного дерева графа G также становится функцией времени t; обозначим эту функцию c_G(t). Возникает естественная задача: найти значение t, при котором минимизируется c_G(t).

Предположим, каждая функция f_e определяется многочленом степени 2: f_e(t) = a_et² + b_et + c_e, где a_e > 0. Предложите алгоритм, который получает граф G и набор значений {(a_e, b_e, c_e): e ∈ E} и возвращает значение времени t, при котором минимальное остовное дерево имеет минимальную стоимость. Алгоритм должен выполняться за полиномиальное время в зависимости от количества узлов и ребер графа G. Считайте, что арифметические операции с числами {(a_e, b_e, c_e)} выполняются за постоянное время.

27. В ходе анализа комбинаторной структуры остовных деревьев можно рассмотреть пространство всех возможных остовных деревьев заданного графа и изучить свойства этого пространства. Эта стратегия также применяется во многих похожих задачах.

Один из возможных подходов выглядит так. Пусть G — связный граф, а T и T — два разных остовных дерева графа i. Деревья T и T называются соседями, если T содержит ровно одно ребро, не входящее в T', а T' содержит ровно одно ребро, не входящее в T.

Теперь на базе любого графа G строится (большой) граф H. Узлами H являются остовные деревья G, а ребро между двумя узлами H существует в том случае, если соответствующие остовные деревья являются соседями. Правда ли, что для любого связного графа G полученный граф H является связным? Приведите доказательство того, что граф H всегда связный, или представьте контрпример (с объяснением) связного графа G, для которого граф H не является связным.

28. Предположим, вы работаете на сетевую компанию CluNet, и вам предложена следующая задача. Сеть, над которой в настоящий момент работает компания, моделируется связным графом G= (V, E) с n узлами. Каждое ребро e представляет оптоволоконный кабель, арендуемый CluNet у его владельцев — компаний X и Y. Ваши клиенты хотят выбрать остовное дерево T графа G и обновить каналы, соответствующие ребрам T. Специалисты по деловым отношениям уже заключили с компаниями X и Y договор, в котором указано число k. При выборе дерева T к из его ребер будут принадлежать X, а n-k-1 ребер будут принадлежать Y.

Теперь руководство CluNet столкнулось с проблемой: ему совершенно неочевидно, существует ли остовное дерево T, удовлетворяющее таким критериям, и как найти его, если оно существует. Перед вами поставлена задача: найти алгоритм с полиномиальным временем, который получает граф G с ребрами, помеченными X или Y, и либо (i) возвращает остовное дерево, в котором ровно к ребер помечено X, либо (ii) обоснованно сообщает о том, что такое дерево не существует.

29. Имеется список из n натуральных чисел d₁, d₂, ..., d_n. Покажите, как за полиномиальное время решить, существует ли ненаправленный граф G = (V, E), степени узлов которого равны d₁, d₂, ..., d_n. (То есть если V = {v₁, v₂, ..., v_n}, степень v_i должна быть равна d_i.) Граф G не может содержать нескольких ребер между одной парой узлов, или “циклических” ребер с одинаковыми конечными точками.

30. Граф G = (V, E) содержит n узлов; каждая пара узлов соединяется ребром. Каждому ребру (i, j) присвоен положительный вес w_y; значения весов соответствуют неравенству треугольника w_ik ≤ w_ij + w_jk. Для подмножества V ⊆ V подграф (с весами ребер), определяемый множеством узлов V', обозначается G[V'].

Имеется множество X ⊆ V из k точек, которые должны быть соединены ребрами. Деревом Штейнера для X называется такое множество Z, что X ⊆ Z ⊆ V, в сочетании с остовным поддеревом Tподграфа G[Z]. Весом дерева Штейнера называется вес дерева T.

Покажите, что задача нахождения дерева Штейнера с минимальным весом для X может быть решена за время O(n^O(k)).

31. Вернемся к исходной формулировке задачи нахождения минимального остов- ного дерева: имеется связный ненаправленный граф G = (V, E) с положительными длинами ребер {l_e}; нужно найти для него остовной подграф. Теперь допустим, что нас интересует подграф H = (V, F) c большей “плотностью”, чем у дерева, и с гарантиями того, что для каждой пары вершин u, v ∈ V длина кратчайшего пути u-v в H не намного больше длины кратчайшего пути u-v в G. Под “длиной пути Р” подразумевается сумма l_е по всем ребрам e в P. Следующая разновидность алгоритма Крускала строит такой подграф:

• Ребра сортируются в порядке возрастания длин. (Предполагается, что все длины ребер различны.)

• Затем строится подграф H = (V, F) с последовательным рассмотрением всех ребер.

• При переходе к ребру e = (u, v) ребро e включается в подграф H, если в настоящее время в H не существует пути u-v. (Алгоритм Крускала делал бы то же самое.) С другой стороны, если путь u-v в H существует, обозначим d_uv кратчайший из таких путей (как и прежде, длина определяется значениями {l_e}). Ребро e добавляется в H, если 3l_e < d_uv.

Иначе говоря, ребро добавляется даже в том случае, если и и v уже находятся в одной компоненте связности, — при условии, что добавление ребра в достаточной степени сокращает их расстояние кратчайшего пути.

Пусть H = (V, F) — подграф G, возвращенный алгоритмом.

(a) Докажите, что для каждой пары узлов и, v ∈ V длина кратчайшего пути u-v в H не более чем в три раза превышает длину кратчайшего пути u-v в G.

(b) Несмотря на приближенное сохранение расстояний кратчайших путей, подграф H, произведенный алгоритмом, не должен быть слишком плотным. Пусть f(n) — максимальное количество ребер, которые могут быть получены на выходе алгоритма для всех входных графов из n узлов с длинами ребер. Докажите, что

32. Рассмотрим направленный граф G = (V, E) с корнем r ∈ V и неотрицательными стоимостями ребер. В этой задаче рассматриваются разновидности алгоритма ориентированного дерева с минимальной стоимостью.

(a) Алгоритм, рассмотренный в разделе 4.9, работает следующим образом: мы изменяем стоимости, рассматриваем подграф с ребрами нулевой стоимости, ищем направленный цикл в этом подграфе и сжимаем его (если такой цикл существует). Возможно ли вместо циклов найти и сжать сильные компоненты подграфа? Приведите краткое обоснование.

(b) В алгоритме мы определяли величину y_v как минимальную стоимость ребра, входящего в v, и изменяли стоимости всех ребер e, входящих в узел v, по формуле c'_e = c_e - y_v. Допустим, вместо этого используется следующая модифицированная стоимость: c''_e = max(0, c_e - 2y_v). Вероятно, в результате этого изменения у большего количества ребер стоимость будет равна 0. Теперь предположим, что мы нашли ориентированное дерево T со стоимостью 0. Докажите, что стоимость T не более чем вдвое превышает стоимость ориентированного дерева с минимальной стоимостью в исходном графе.

(c) Предположим, что ориентированное дерево со стоимостью 0 не найдено. Сожмите все сильные компоненты со стоимостью 0 и рекурсивно примените ту же процедуру к полученному графу, пока не будет найдено ориентированное дерево. Докажите, что стоимость T не более чем вдвое превышает стоимость ориентированного дерева с минимальной стоимостью в исходном графе.

33. Имеется направленный граф G = (V, E), в котором стоимость каждого ребра равна либо 0, либо 1. Предположим, в G имеется такой узел r, что существует путь от r к любому другому узлу G. Также дано целое число k. Приведите алгоритм с полиномиальным временем выполнения, который либо строит ориентированное дерево с корнем r, стоимость которого равна точно k, либо обоснованно сообщает о том, что такое дерево не существует.

Примечания и дополнительная литература

Благодаря своей концептуальной четкости и интуитивной привлекательности, жадные алгоритмы изучаются уже давно и нашли множество применений в компьютерных науках. В этой главе основное внимание уделялось ситуациям, для которых жадный алгоритм находит оптимальное решение. Жадные алгоритмы также часто используются в качестве простых эвристик даже тогда, когда оптимальность решения не гарантирована. В главе 11 рассматриваются жадные алгоритмы, которые находят решения, близкие к оптимальным.

Как упоминалось в главе 1, задача интервального планирования может рассматриваться как частный случай задачи поиска независимого множества для графа, представляющего перекрытия в наборе интервалов. Графы, которые встречаются в таких задачах, называются интервальными графами и были тщательно изучены; за информацией, например, обращайтесь к книге Голамбика (Golumbic, 1980). Не только задача поиска независимого множества, но и многие другие вычислительные задачи существенно упрощаются для особого случая интервальных графов.

Задача интервального планирования и задача планирования для минимизации максимальной задержки — два представителя категории базовых задач планирования, для которых простой жадный алгоритм выдает оптимальное решение. Описания многих других взаимосвязанных задач можно найти в работе Лоулера, Ленстры, Ринноя Кана и Шмойса (Lawler, Lenstra, Rinnoy Kanand Shmoys, 1993).

Автором оптимального алгоритма кэширования и его анализа является Белади (Belady, 1966). Как упоминалось в тексте, в реальных условиях алгоритмы кэширования должны применять решения по вытеснению в реальном времени, без информации о будущих запросах. Такие стратегии кэширования будут рассматриваться в главе 13.

Алгоритм нахождения кратчайших путей в графе с неотрицательными длинами ребер предложил Дейкстра (Dijkstra, 1959). Обзоры методов решения задачи минимального остовного дерева (вместе с историческим обзором) можно найти в статьях Грэма и Хелла (Graham, Hell, 1985) и Несетрила (Nesetril, 1997).

Алгоритм одиночной связи является одним из самых распространенных подходов к общей задаче кластеризации; в книгах Андерберга (Anderberg, 1973), Дуды, Харта и Сторка (Duda, Hart, Stork, 2001), а также Джейна и Дьюбса (Jain, Dubes, 1981) представлены различные методы кластеризации.

Алгоритм построения оптимальных префиксных кодов разработан Хаффманом (Huffman, 1952); более ранние методы, упоминаемые здесь, встречаются в книгах Фано (Fano, 1949), а также Шеннона и Уивера (Shannon, Weaver, 1949). Общий обзор методов сжатия данных приведен в книге Белла, Клири и Уиттен (Bell, Cleary, Witten, 1990), а также в статье Лелевера и Хиршберга (Lelewer, Hirschberg, 1987). В более общем смысле эта тема относится к теории передачи информации, занимающейся методами представления и кодирования цифровых данных. Одной из фундаментальных работ в этой области является книга Шеннона и Уивера (Shannon, Weaver, 1949); в более позднем учебнике Кавера и Томаса (Cover, Thomas, 1991) приводится подробная информация по теме.

Авторами алгоритма нахождения ориентированного дерева с минимальной стоимостью обычно называют Чу и Лю (Chu, Liu, 1965) и Эдмондсу (Edmonds, 1967), разработавших его независимо друг от друга. Как упоминалось в главе, этот многофазный метод расширяет наши представления о том, что собой представляет жадный алгоритм. Он также важен с точки зрения линейного программирования, поскольку в этом контексте может рассматриваться как фундаментальное практическое применение метода ценообразования, или прямодвойственного метода (primal-dualtechnique), при разработке алгоритмов. Книга Немхаузера и Волси (Nemhauser, Wolsey, 1988) развивает эти связи с линейным программированием. Метод будет описан в главе 11 в контексте аппроксимирующих алгоритмов.

Как было сказано в начале главы, трудно дать точное определение того, что же следует считать жадным алгоритмом. В поисках такого определения даже непонятно, можно ли провести аналогию со знаменитым критерием непристойности судьи Стюарта из Верховного суда США (“Когда я её вижу, я знаю, что это такое”), поскольку в научном сообществе нет единой точки зрения (и даже интуитивных представлений) относительно границы между жадными и нежадными алгоритмами. Проводились исследования, направленные на формализацию классов жадных алгоритмов: из примеров можно упомянуть влиятельную теорию матроидов (Edmonds, 1971; Lawer, 2001). В статье Бородина, Нильсена и Ракоффа (Borodin, Nielsen, Rackoff, 2002) формализуются понятия жадных алгоритмов и алгоритмов “жадного типа”, а также приводятся сравнения с другими теоретическими работами по данному вопросу.

Примечания к упражнениям

Упражнение 24 основано на результатах, авторами которых были М. Эдахиро, Т. Чао, И. Сюй, Дж. Хо, К. Безе и А. Канг; упражнение 31 основано на результатах, авторами которых были Инго Альтхофер, Гаутам Дас, Дэвид Добкин и Дебора Джозеф.

---

¹ Также встречается название “задача интервального окрашивания”; термин происходит от представления о ресурсах как об окрашенных в разные цвета — всем интервалам, назначаемым конкретному ресурсу, присваивается соответствующий цвет.