Ориентированные деревья с минимальном стоимостью: многофазный жадный алгоритм - Жадные алгоритмы

Мы рассмотрели уже много примеров жадных алгоритмов. Как вы могли убедиться, принципы их работы основательно различаются. Многие жадные алгоритмы принимают решение об исходной “упорядоченности” своих входных данных, а затем обрабатывают все за один проход. Другие алгоритмы принимают большее количество пошаговых решений — также локальных и “недальновидных”, не подчиненных некоему “глобальному плану”. В этом разделе будет рассмотрена задача, которая расширит ваши интуитивные представления о жадных алгоритмах.

Задача

Требуется вычислить для направленного графа ориентированное дерево с минимальной стоимостью. Фактически это аналог задачи нахождения минимального остовного дерева для направленных графов; как вы убедитесь, переход к направленным графам значительно усложняет ситуацию. В то же время алгоритм ее решения сильно напоминает другие жадные алгоритмы, потому что решение строится по локальному, недальновидному правилу.

Начнем с базовых определений. Пусть G = (V, E) — направленный граф, в котором один узел r ∈ V выделен как корневой. Ориентированное дерево (по отношению к r) фактически представляет собой направленное остовное дерево с корнем в r. А конкретнее — это такой подграф T = (V, F), что T является остовным деревом графа G, если не считать направленности ребер; и существует путь T из r к каждому другому узлу v ∈ V, если учитывать направленность ребер. На рис. 4.18 приведен пример двух разных ориентированных деревьев одного направленного графа.

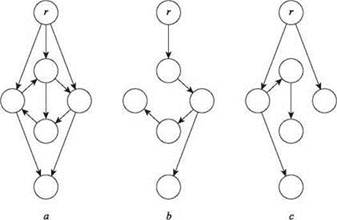
Рис. 4.18. Направленный граф может иметь много разных ориентированных деревьев. На рис. b и c изображены два разных ориентированных дерева с корнем в узле r для графа a

Существует полезный эквивалентный способ описания ориентированных деревьев.

(4.34) Подграф T = (V, F) графа G является ориентированным деревом по отношению к корню r в том и только в том случае, если T не содержит циклов и для каждого узла v ≠ r существует ровно одно ребро из F, входящее в v.

Доказательство. Если T — ориентированное дерево с корнем r, то в любой другой узел v входит ровно одно ребро: это просто последнее ребро уникального пути r-v.

И наоборот, допустим, T не содержит циклов, а каждый узел v = r имеет ровно одно входное ребро. Чтобы установить, что T является ориентированным деревом, достаточно показать, что существует направленный путь от г к любому другому узлу v. Этот путь строится следующим образом: мы начинаем с v и последовательно переходим по ребрам в обратном направлении. Так как T не содержит циклов, мы никогда не вернемся к ранее посещенному узлу, а следовательно, этот процесс должен завершиться. Но r — единственный узел без входных ребер, поэтому процесс должен завершиться с достижением r; последовательность посещенных узлов образует путь (в обратном направлении) от r к v. ■

По аналогии с тем, как у каждого связного графа существует остовное дерево, направленный граф имеет ориентированное дерево с корнем r при условии, что из r можно достигнуть любого узла. Действительно, в этом случае ребра дерева поиска в ширину с корнем r образуют ориентированное дерево.

(4.35) В направленном графе G существует ориентированное дерево с корнем r в том, и только в том случае, если существует направленный путь от r к любому другому узлу.

Базовая задача, которую мы здесь рассматриваем, такова: имеется направленный граф G = (V, E) с выделенным корневым узлом r и неотрицательной стоимостью c_e ≥ 0 каждого ребра. Требуется вычислить ориентированное дерево с корнем r и минимальной суммарной стоимостью (оно будет называться оптимальным ориентированным деревом). В дальнейшем будем считать, что G по крайней мере содержит ориентированное дерево с корнем r; согласно (4.35), это можно легко проверить с самого начала.

Разработка алгоритма

С учетом отношений между деревьями и ориентированными деревьями задача нахождения ориентированного дерева с минимальной стоимостью, конечно, сильно напоминает задачу нахождения минимального остовного дерева для ненаправленных графов. Следовательно, будет естественно для начала поинтересоваться, нельзя ли напрямую применить идеи, разработанные для той задачи, в этой ситуации. Например, должно ли ориентированное дерево с минимальной стоимостью содержать ребро с наименьшей стоимостью во всем графе? Можно ли безопасно удалить самое “дорогостоящее” ребро в цикле и быть полностью уверенным в том, что оно отсутствует в оптимальном ориентированном дереве?

Разумеется, ребро с наименьшей стоимостью в G не будет принадлежать оптимальному ориентированному дереву, если e входит в корневой узел, поскольку искомое ориентированное дерево не должно иметь ребер, входящих в корень. Но даже если ребро с наименьшей стоимостью в G принадлежит ориентированному дереву с корнем г, оно не обязательно принадлежит оптимальному, как показывает пример на рис. 4.19. Действительно, включение ребра со стоимостью 1 на рис. 4.19 не позволит включить ребро со стоимостью 2 из корня r (так как узел может иметь только одно входное ребро), а это, в свою очередь, приводит к неприемлемой стоимости 10 при включении другого ребра из г. Такие аргументы никогда не затрудняли решение задачи минимального остовного дерева, в которой всегда было безопасно включить ребро с минимальной стоимостью; это наводит на мысль, что поиск оптимального ориентированного дерева может быть намного более сложной задачей. (Стоит заметить, что оптимальное ориентированное дерево на рис. 4.19 также включает ребро цикла с максимальной стоимостью; при другой структуре оптимальное ориентированное дерево даже может содержать ребро с наибольшей стоимостью во всем графе.)

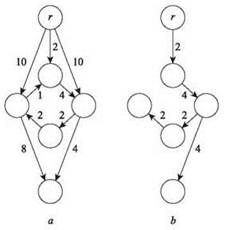
Рис. 4.19. a — направленный граф с обозначенной стоимостью ребер; и b — оптимальное ориентированное дерево с корнем в узле r этого графа

Несмотря на все сложности, для этой задачи можно спроектировать алгоритм жадного типа, просто наше недальновидное правило выбора ребер должно быть чуть более сложным. Для начала разберемся, почему не работает общая стратегия включения ребер с наименьшей стоимостью. Формальное описание этой стратегии выглядит так: для каждого узла v ≠ r выбирается ребро с минимальной стоимостью, входящее в v (с произвольной разбивкой “ничьих”); обозначим это множество из n - 1 ребер F*. Рассмотрим подграф (V, F*). Так как мы знаем, что оптимальное ориентированное дерево должно иметь ровно одно ребро, входящее в каждый узел v ≠ r, а (V, F*) представляет способ принятия решений с минимальной стоимостью, мы приходим к следующему факту.

(4.36) Если (V, F*) — ориентированное дерево, то это ориентированное дерево с минимальной стоимостью.

Итак, сложность в том, что (V, F*) может и не быть ориентированным деревом. В этом случае из (4.34) следует, что в (V, F*) должен присутствовать цикл C, не включающий корень. Теперь нужно решить, что делать в такой ситуации.

Чтобы рассуждения стали более понятными, начнем со следующего наблюдения. Каждое ориентированное дерево содержит ровно одно ребро, входящее в каждый узел v ≠ r; если выбрать некоторое ребро v и вычесть постоянную величину из стоимости каждого ребра, входящего в v, то общая стоимость каждого ориентированного дерева изменится на одинаковую величину. По сути, это означает, что фактическая стоимость всех остальных ребер, входящих в v, относительна этой величины. Пусть yv означает минимальную стоимость любого ребра, входящего в v. Для каждого ребра е = (и, v) со стоимостью с_е ≥ 0 определяется модифицированная стоимость с_e', равная с_e – у_v. Поскольку с_e ≥ у_v, все модифицированные стоимости остаются неотрицательными. Но важнее то, что из этого вытекает следующий факт.

(4.37) T является оптимальным ориентированным деревом в G со стоимостями {c_e} в том, и только в том случае, если оно также является оптимальным ориентированным деревом с модифицированными стоимостями {c'_e}.

Доказательство. Возьмем произвольное ориентированное дерево Т. Разность между его стоимостью с набором стоимостей {c_e} и {с'е} равна в точности то есть

Это объясняется тем, что у ориентированного дерева в каждый узел v из суммы входит ровно одно ребро. Поскольку разность между двумя ребрами не зависит от выбора ориентированного дерева T, мы видим, что граф T имеет минимальную стоимость с {c_e} в том, и только в том случае, если он имеет минимальную стоимость с {c'_e}. ■

Теперь рассмотрим задачу в контексте стоимостей {c'_e}. Все ребра в множестве F имеют стоимость 0 с модифицированными стоимостями; таким образом, если (V, F*) содержит цикл C, мы знаем, что стоимость всех ребер в C равна 0. Из этого следует, что мы можем использовать сколько угодно ребер из C (не нарушающих правила построения ориентированного дерева), поскольку включение ребер из C не повышает стоимость.

В продолжение работы алгоритма C свертывается в один суперузел с формированием меньшего графа G' = (V', E'). Здесь V' содержит узлы V - C плюс один узел c*, представляющий C. Каждое ребро e ∈ E преобразуется в ребро e' ∈ E' заменой каждого конца е, принадлежащего C, новым узлом c*. В результате у G' могут появиться параллельные ребра (то есть ребра с одинаковыми концами), это нормально; однако из E' удаляются петли — ребра, у которых оба конца равны c* В этом уменьшенном графе G' со стоимостями {c'_e} проводится рекурсивный поиск оптимального ориентированного дерева. Ориентированное дерево, возвращаемое рекурсивным вызовом, может быть преобразовано в ориентированное дерево графа G включением всех ребер цикла C, кроме одного.

Ниже приводится полный алгоритм.

Анализ алгоритма

Этот алгоритм легко реализовать так, чтобы он выполнялся за полиномиальное время. Но приведет ли он к оптимальному ориентированному дереву? Прежде чем делать такой вывод, необходимо учесть одно обстоятельство: не каждое ориентированное дерево в G соответствует ориентированному дереву в свернутом графе G'. Не могли ли мы “упустить” настоящее оптимальное ориентированное дерево в G, сосредоточившись на G'?

Ориентированные деревья G' однозначно соответствуют ориентированным деревьям G, которые имеют ровно одно ребро, входящее в цикл C; и эти соответствующие ориентированные деревья имеют одинаковую стоимость в отношении {с'_е}, потому что C состоит из ребер стоимости 0. (Мы говорим, что ребро е = (u, v) входит в C, если v принадлежит C, а и не принадлежит.) Итак, чтобы доказать, что наш алгоритм находит оптимальное ориентированное дерево в G, необходимо доказать, что G имеет оптимальное ориентированное дерево с ровно одним ребром, входящим в C. Сейчас мы это сделаем.

(4.38) Пусть C — цикл в G, состоящий из ребер со стоимостью 0, такой, что r ∉ C. Тогда существует оптимальное ориентированное дерево с корнем г, в котором в C входит ровно одно ребро.

Доказательство. Рассмотрим оптимальное ориентированное дерево T в G. Так как в T от r существует путь к каждому узлу, существует как минимум одно ребро в T, которое входит в C. Если Tвходит в C ровно один раз, дело сделано. В противном случае предположим, что T входит в С многократно. Мы покажем, как изменить его для получения ориентированного дерева с не большей стоимостью, которое входит в C ровно один раз.

Пусть е = (a, b) — ребро, входящее в C, которое лежит на самом коротком возможном пути от r. В частности, это означает, что никакие ребра на пути от r не могут входить в C. Удалим все ребра T, входящие в C, кроме ребра е. Добавим во все ребра C, кроме ребра, входящего в b, — конец ребра е. Полученный подграф G обозначим T'.

Утверждается, что T' также является ориентированным деревом. Если утверждение истинно, мы приходим к желаемому результату, поскольку стоимость T' очевидно не больше стоимости T: единственные ребра T', которые не принадлежат также T, имеют стоимость 0. Почему же T является ориентированным деревом?

Заметим, что у T ровно одно ребро входит в каждый узел v ≠ r, и никакое ребро не входит в r. Следовательно, T содержит ровно n - 1 ребро; если нам удастся показать, что для каждого v в T' существует путь r-v, то граф T должен быть связным в ненаправленном смысле, а следовательно, является деревом. Это означает, что он удовлетворяет исходному определению ориентированного дерева.

Итак, рассмотрим любой узел v = r; мы должны показать, что в T существует путь г-v. Если v ∈ C, можно использовать тот факт, что путь в T от r к е был сохранен при конструировании T'; значит, чтобы достигнуть v, нужно сначала перейти к е, а потом следовать по ребрам цикла C. Теперь предположим, что v $ C, и введем обозначение P для пути r-v в T. Если путь P не касается C, то он существует и в T'. В противном случае пусть w — последний узел в P ∩ C, а P' — подпуть P от w к v. Заметьте, что все ребра в P' также существуют в T'. Ранее уже было показано, что узел w достижим из r в T', потому что он принадлежит C. Объединяя этот путь к w с подпутем P', мы получаем путь к v. ■

Теперь можно собрать все воедино и убедиться в правильности алгоритма.

(4.39) Алгоритм находит оптимальное ориентированное дерево с корнем r в графе G.

Доказательство. Воспользуемся индукцией по количеству узлов в G. Если ребра F образуют ориентированное дерево, то алгоритм вернет оптимальное ориентированное дерево согласно (4.36). В противном случае рассмотрим задачу с модифицированными стоимостями {с'е}, эквивалентную согласно (4.37). После свертки цикла C со стоимостью 0 для получения меньшего графа G' алгоритм создает оптимальное ориентированное дерево в G' согласно индукционной гипотезе. Наконец, согласно (4.38), в G существует оптимальное ориентированное дерево, соответствующее оптимальному ориентированному дереву, вычисленному для G'. ■