Выравнивание последовательностей в линейном пространстве по принципу разделяй и властвуй - Динамическое программирование

В предыдущем разделе был рассмотрен процесс вычисления оптимального выравнивания между двумя строками X и Y длины m и n соответственно. Построение двумерного массива m ^х nоптимальных решений подзадач, OPT(-, -), оказалось эквивалентным построению графа О_ху с mn узлами, образующими решетку, и поиску пути наименьшей стоимости между противоположными углами. В каждом из этих способов формулировки алгоритма динамического программирования время выполнения равно O(mn), потому что значение каждой из mn ячеек массива OPT определяется за постоянное время; затраты памяти также равны O(mn), потому что в них доминируют затраты на хранение массива (или графа G_XY).

Задача

В этом разделе мы зададимся следующим вопросом: следует ли удовольствоваться границей затрат памяти O(mn)? Если приложение сравнивает слова (или даже предложения) английского языка, такие затраты вполне приемлемы. Однако в биологических задачах выравнивания последовательностей часто приходится сравнивать очень длинные строки и в таких ситуациях затраты памяти Ө(mn) могут стать гораздо более серьезной проблемой, чем время Ө(mn). Например, допустим, что сравниваются две строки, каждая из которых состоит из 100 000 символов. В зависимости от процессора перспектива выполнения примерно 10 миллиардов примитивных операций вызывает меньше беспокойства, чем перспектива работы с одним 10-гигабайтным массивом.

В этом разделе будет описано очень умное усовершенствование алгоритма выравнивания последовательностей, с которым работа будет выполняться за время O(mn), тогда как затраты памяти будут составлять только O(m + n). Другими словами, затраты памяти сокращаются до линейных, тогда как время выполнения возрастает не более чем с постоянным множителем. Для простоты изложения шаги алгоритма будут описываться в контексте путей на графе G_XY — естественного эквивалента задачи выравнивания последовательностей. Таким образом, задача поиска пар в оптимальном выравнивании может быть сформулирована как задача поиска ребер в кратчайшем пути из угла в угол графа G_XY.

Сам алгоритм является удачным практическим применением принципа “разделяй и властвуй”. В его основе лежит один важный факт: при делении задачи на несколько рекурсивных вызовов память, необходимая для вычислений, может использоваться для других вызовов. Впрочем, эта идея применяется достаточно нетривиальным образом.

Разработка алгоритма

Сначала мы покажем, что если интерес представляет только значение оптимального выравнивания, а не само выравнивание, обойтись линейными затратами памяти несложно. Дело в том, что для заполнения элемента массива A рекуррентному отношению из (6.15) необходима только информация из текущего столбца A и предыдущего столбца A. Это позволяет “свернуть” массив A в массив B с размерами m х 2: при переборе алгоритмом значений j элементы вида B[i, 0] содержат значение “предыдущего” столбца A[i, j - 1], а элементы вида B[i, 1] — значение “текущего” столбца A[i, j].

Как нетрудно убедиться, при завершении этого алгоритма элемент массива B[i, 1] содержит значение OPT(i, n) для i = 0, 1, ..., m. Кроме того, затраты времени этого алгоритма равны O(mn), а затраты памяти — O(m). Но тут возникает проблема: как получить само выравнивание? Мы не располагаем достаточной информацией для выполнения такой процедуры, как Find-Alignment. Так как B в конце работы алгоритма содержит только последние два столбца исходного массива A, при попытке обратного отслеживания доступная информация ограничивается этими двумя столбцами. Можно попытаться обойти эту сложность “прогнозированием” выравнивания в процессе выполнения процедуры, эффективной по затратам памяти. В частности, при вычислении значений j-го столбца (теперь неявно заданного) массива A можно предположить, что при очень малом значении некоторого элемента выравнивание, проходящее через этот элемент, является перспективным кандидатом на роль оптимального. Но у этого перспективного выравнивания могут возникнуть большие проблемы в будущем, и оптимальным может оказаться другое выравнивание, которое в данный момент выглядит далеко не так перспективно.

На самом деле у этой задачи имеется решение (само выравнивание можно восстановить с затратами памяти O(m + n)), но оно требует совершенно нового подхода, основанного на применении принципа “разделяй и властвуй”, представленного в книге ранее. Начнем с простого альтернативного пути реализации базового решения, построенного по принципам динамического программирования.

Обратная формулировка динамического программирования

Вспомните, что запись f(i, j) использовалась для обозначения длины кратчайшего пути из (0, 0) в (i, j) в графе G_XY. (Как было показано в исходном варианте алгоритма выравнивания последовательностей, f(i, j) имеет то же значение, что и OPT(i, j)). Теперь определим g(i, j) как длину кратчайшего пути из (i, j) в (m, n) в G_xy. Функция g предоставляет столь же естественный подход к решению задачи выравнивания последовательностей методом динамического программирования, не считая того, что на этот раз решение строится в обратном порядке: мы начинаем с g(m, n) = 0, а искомым ответом является g(0, 0).

По строгой аналогии с (6.16) имеем следующее рекуррентное отношение для g:

(6.18) Для i < m и j < n

Это же рекуррентное отношение будет получено, если взять граф “развернуть” его так, чтобы узел (m, n) находился в левом нижнем углу, и воспользоваться приведенным выше методом. По этой схеме также можно проработать полный алгоритм динамического программирования для построения значений g в обратном направлении, начиная с (m, n). Также существует версия этого обратного алгоритма динамического программирования, эффективная по затратам памяти (аналог описанного выше алгоритма), которая вычисляет значение оптимального выравнивания с затратами памяти, не превышающими O(m + n). Эта обратная версия далее будет обозначаться именем Backward-Space-Efficient-Alignment.

Объединение прямой и обратной формулировок

Итак, у нас имеются симметричные алгоритмы для построения значений функций f и g. Идея заключается в том, чтобы использовать эти два алгоритма совместно для поиска оптимального выравнивания. Прежде всего стоит выделить два основных факта, характеризующих отношения между функциями f и g.

(6.19) Длина кратчайшего пути из угла в угол в G_xy проходящего через (i, j), равна f(i, j) + g(i, j).

Доказательство. Пусть l_ij — длина кратчайшего пути из угла в угол, проходящего через (i, j). Очевидно, что любой такой путь должен перейти от (0,0) к (i, j), а затем от (i, j) к (m, n). Следовательно, его длина равна как минимум f(i, j) + g(i, j), а значит, l_ij ≥ f(i, j) + g(i, j). С другой стороны, рассмотрим путь из угла в угол, состоящий из пути минимальной длины из (0, 0) в (i, j), за которым следует путь минимальной длины из (i, j) в (m, n). Длина этого пути равна f(i, j) + g(i, j), поэтому l_ij ≤ f(i, j) + g(i, j). Из этого следует, что l_ij = f(i, j) + g(i, j). ■

(6.20) Пусть k — произвольное число из диапазона {0, ..., n}, а q — индекс, минимизирующий величину f(q, k) + g(q, k). В этом случае существует путь минимальной длины из угла в угол, проходящий через узел (q, k).

Доказательство. Пусть l* — длина кратчайшего пути из угла в угол в G_xy. Зафиксируем значение k ∈ {0, ..., n}. Кратчайший путь из угла в угол должен проходить через какой-то из узлов k-го столбца G_XY — предположим, это узел (р, k), — а следовательно, из (6.19)

Рассмотрим индекс q, с которым достигается минимум в правой стороне этого выражения; имеем

Снова согласно (6.19) кратчайший путь из угла в угол, использующий узел (q, k), имеет длину f(q, k) + g(q, k), а поскольку l* является минимальной длиной среди всех путей из угла в угол,

Следовательно, l* = f(q, k) + g(q, k). Таким образом, кратчайший путь из угла в угол, использующий узел (q, k), имеет длину l*, что доказывает (6.20). ■

Используя (6.20) и наши алгоритмы, эффективные по затратам памяти, для вычисления значения оптимального выравнивания, продолжим следующим образом: разделим G_XY по центральному столбцу и вычислим значение f(i, n/2) и g(i, n/2) для каждого значения i, используя два алгоритма, эффективные по затратам памяти. Затем можно определить минимальное значение f(i, n/2) + g(i, n/2) и с учетом (6.20) сделать вывод о существовании кратчайшего пути из угла в угол, проходящего через узел (i, n/2). В этих условиях можно провести рекурсивный поиск кратчайшего пути в части G_XY между (0,0) и (i, n/2) и в части между (i, n/2) и (m, n). Здесь принципиально то, что мы применяем эти рекурсивные вызовы последовательно и повторно используем рабочее пространство памяти между вызовами. А поскольку мы работаем только с одним рекурсивным вызовом за раз, общие затраты памяти составят O(m + n). Остается ответить на ключевой вопрос: останется ли время выполнения этого алгоритма равным O(mn)?

При выполнении алгоритма ведется глобально доступный список P, в котором сохраняются узлы кратчайшего пути из угла в угол по мере их обнаружения. Изначально список P пуст. Он состоит из m + n элементов, поскольку ни один путь из угла в угол не может содержать большего количества узлов. Используем следующие обозначения: X[i: j] для 1 ≤ i ≤ j ≤ m обозначает подстроку X, состоящую из x_ix_i+1 ... x_j; аналогичным образом определяется Y[i: j]. Для простоты будем считать, что n является степенью 2; это предположение существенно упрощает анализ, хотя при желании его легко можно снять.

Пример первого уровня рекурсии представлен на рис. 6.19. Если минимизирующий индекс q оказывается равным 1, мы получаем две изображенные подзадачи.

Анализ алгоритма

Приведенные выше рассуждения уже доказывают, что алгоритм возвращает правильный ответ и использует память O(m + n). Остается проверить только следующий факт.

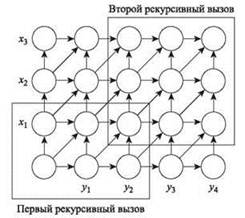
Рис. 6.19. Первый уровень рекуррентности для процедуры Divide-and-Conquer-Alignment, эффективной по затратам памяти. Две области, выделенные рамкой, обозначают входные данные для двух рекурсивных вызовов

(6.21) Время выполнения для процедуры Divide-and-Conquer-Alignment для строк длины m и n равно O(mn).

Доказательство. Обозначим T(m, n) максимальное время выполнения алгоритма для строк m и n. Алгоритм выполняет работу O(mn) для построения массивов B и B'; затем он рекурсивно выполняется для строк c размерами q и n/2 и строк с размерами m - q и n/2. Следовательно, для некоторой константы c и некоторого выбора индекса q:

Эта рекуррентность сложнее тех, которые встречались нам ранее в примерах “разделяй и властвуй” из главы 5. Прежде всего, время выполнения является функцией двух переменных (m и n), а не одной; кроме того, разбиение на подзадачи не обязательно является “равным”, а зависит от значения q, найденного в ходе предшествующей работы, выполненной алгоритмом.

Как же подойти к разрешению этой рекуррентности? Можно попытаться угадать форму решения, рассмотрев частный случай рекуррентности, и затем воспользоваться частичной подстановкой для заполнения параметров. А именно предположим, что m = n, а точка разбиения q находится точно в середине. В этом (надо признаться, весьма ограниченном) частном случае мы можем записать функцию T(∙) для одной переменной n, присвоить q = n/2 (предполагается идеальное деление пополам) и прийти к условию

T(n) ≤ 2Т(n/2) + cn².

Это выражение полезно, потому что оно уже было разрешено при обсуждении рекуррентности в начале главы 5, а именно: из этой рекуррентности следует T(n) = O(n²).

Итак, при m = n и равном разбиении время выполнения возрастает в квадратичной зависимости от n. Вооружившись этой информацией, мы возвращаемся к общему рекуррентному отношению текущей задачи и предполагаем, что T(m, n) растет со скоростью произведения m и n. А именно предположим, что T(m, n) ≤ kmn для некоторой константы k, и посмотрим, удастся ли доказать это утверждение по индукции. Начиная с базовых случаев m ≤ 2 и n ≤ 2, мы видим, что они выполняются при k ≥ с/2. Теперь предполагая, что T(m', n') ≤ km'n' выполняется для пар (m', n') с меньшим произведением, имеем

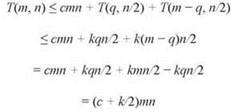
Следовательно, шаг индукции выполняется, если выбрать k = 2c, а доказательство на этом завершается. ■