Кратчайшие пути в графе - Динамическое программирование

В трех последних разделах этой главы мы займемся задачей нахождения кратчайших путей в графе, а также другими вопросами, тесно связанными с этой темой.

Задача

Имеется направленный граф G = (V, E), каждому ребру которого (i, j) ∈ E присвоен вес c_ij. Веса могут моделировать самые разные характеристики; в нашей интерпретации вес c_ij представляет стоимость прямого перехода от узла i к узлу j в графе.

Ранее мы уже обсуждали алгоритм Дейкстры для нахождения кратчайших путей в графах с положительной стоимостью ребер. Здесь рассматривается более сложная задача нахождения кратчайших путей, в которых стоимости могут быть отрицательными. Решение этой задачи актуально во многих ситуациях, среди которых особенно важны две. Во-первых, отрицательные стоимости играют ключевую роль при моделировании некоторых процессов с кратчайшими путями: например, узлы могут представлять агентов в финансовых отношениях, а с_ij — стоимость операции, в которой вы покупаете у агента i, а затем немедленно продаете агентуj. В этом случае путь представляет серию операций, а ребра с отрицательной стоимостью — операции, приносящие прибыль. Во-вторых, алгоритм, который мы разработаем для обработки ребер с отрицательной стоимостью, во многих важных отношениях оказывается более гибким и децентрализованным, чем алгоритм Дейкстры. Как следствие, он находит важное применение при проектировании алгоритмов распределенной маршрутизации, определяющих наиболее эффективный путь в сети передачи данных.

В этом и двух следующих разделах рассматриваются две взаимосвязанные задачи:

♦ Для заданного графа G с весами (см. выше) решить, существует ли в G отрицательный цикл, то есть направленный цикл C, для которого

♦ Если граф не содержит отрицательных циклов, найти путь P от начального узла s к конечному узлу t с минимальной общей стоимостью; сумма

должна быть минимально возможной для любого пути s—t. Обычно эта задача называется как задачей нахождения пути с минимальной стоимостью, так и задачей нахождения кратчайшего пути.

В приведенном выше финансовом примере отрицательный цикл соответствует прибыльной серии операций, которая возвращается к начальной точке: мы покупаем у i₁ продаем i₂, покупаем у i₃и т. д., в итоге возвращаясь к i₁ с чистой прибылью. Отрицательные циклы в таких сетях могут стать поводом для обращения в арбитраж.

Задачу нахождения пути s-t с минимальной стоимостью стоит рассматривать в предположении об отсутствии отрицательных циклов. Как показано на рис. 6.20, если бы в графе существовал отрицательный цикл C, путь P_s от s к циклу и другой путь P_t от цикла к t позволил бы построить путь s-t с произвольной отрицательной стоимостью: сначала по P_s переходим к отрицательному циклу C, “крутимся” в цикле сколько угодно раз и, наконец, используем P_t для перехода от C к конечному узлу t.

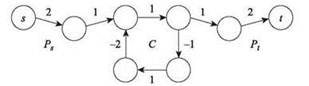
Рис. 6.20. В этом графе присутствуют пути s-t с произвольной отрицательной стоимостью (с многократным прохождением цикла C)

Разработка и анализ алгоритма

Несколько неудачных попыток

Для начала припомним алгоритм Дейкстры для нахождения кратчайшего пути при отсутствии ребер с отрицательной стоимостью. Этот метод вычисляет кратчайший путь от начальной точки s до любого другого узла v в графе, фактически с использованием жадного алгоритма. Основная идея заключается в построении такого множества S, для которого известен кратчайший путь от s к каждому узлу S. Работа начинается с S = {s} (мы знаем, что при отсутствии отрицательных ребер кратчайший путь из s в s имеет стоимость 0), после чего начинается жадное добавление элементов в множество S. На первом жадном шаге рассматривается ребро минимальной стоимости, выходящее из узла i, то есть Пусть v — узел, для которого достигается минимум. Ключевой факт, заложенный в основу алгоритма Дейкстры, заключается в том, что кратчайшим путем из s в v является путь из одного ребра {s, v}. Следовательно, узел v можно немедленно добавить в множество S. Путь {s, v} очевидно является кратчайшим путем к v при отсутствии ребер с отрицательной стоимостью: любой другой путь из s в v должен начинаться с ребра, выходящего из s, стоимость которого по крайней мере не меньше стоимости ребра (s, v).

Если ребра могут иметь отрицательную стоимость, это рассуждение перестает быть истинным. Как подсказывает пример на рис. 6.21, а, путь, начинающийся с ребра с высокой стоимостью, которая компенсируется последующими ребрами с отрицательной стоимостью, может быть “дешевле” пути, начинающегося с ребра низкой стоимости. Следовательно, жадный метод в стиле алгоритма Дейкстры здесь не сработает.

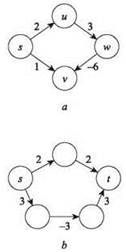
Рис. 6.21. а — с отрицательной стоимостью ребер алгоритм Дейкстры может дать неверный ответ на задачу кратчайшего пути; b — при увеличении стоимости каждого ребра на 3 стоимости всех ребер становятся неотрицательными, но при этом изменяется кратчайший путь s-t

Другая естественная идея — выполнить предварительное изменение стоимостей ребер с_ij, прибавив к каждой некоторую большую константу M; иначе говоря, для каждого ребра (i, j) ∈ Eвыполняется с'_ij = с_ij + M. Если константа M достаточно велика, все измененные стоимости будут неотрицательными, и мы сможем воспользоваться алгоритмом Дейкстры для нахождения пути с минимальной стоимостью, складывающейся из с'. Тем не менее этот метод не всегда находит правильный путь с минимальной стоимостью в отношении исходных стоимостей с. Дело в том, что изменение стоимости с с на с' изменяет путь с минимальной стоимостью. Например (как показано на рис. 6.21, b), если стоимость пути P, состоящего из трех ребер, лишь ненамного меньше стоимости другого пути P', состоящего из двух ребер, то после изменения стоимостей P' станет “дешевле”, потому что стоимость P' увеличивается на 2M, а стоимость P — на 3M.

Решение методом динамического программирования

Попробуем воспользоваться динамическим программированием для решения задачи поиска кратчайшего пути из s в t при наличии отрицательных стоимостей ребер, но без отрицательных циклов. Также можно опробовать идею, которая работала в прошлом: подзадача i может искать кратчайший путь с использованием только первых i узлов. Эта идея не работает немедленно, но ее можно заставить работать ценой некоторых усилий. А здесь мы рассмотрим более простое и эффективное решение — алгоритм Беллмана-Форда. Разработку динамического программирования как общей алгоритмической методологии часто приписывают работе Беллмана, опубликованной в 1950-х годах; а алгоритм нахождения кратчайшего пути Беллмана-Форда стал одним из ее первых практических применений.

Решение из области динамического программирования, которое мы разработаем, будет основано на следующем ключевом факте.

Рис. 6.22. Путь с минимальной стоимостью P из v в t, использующий не более i ребер

(6.22) Если граф G не содержит отрицательных циклов, то существует кратчайший путь из s в t, который является простым (то есть не содержит повторяющихся узлов), а следовательно, содержит не более n - 1 ребер.

Доказательство. Так как каждый цикл имеет неотрицательную стоимость, в кратчайшем пути P из s в t с наименьшим числом ребер не повторяется никакая вершина v. Если бы в P повторялась вершина v, то мы могли бы удалить часть P между последовательными посещениями v, что привело бы к построению пути с не большей стоимостью и меньшим количеством ребер.

Воспользуемся OPT(i, v) для обозначения минимальной стоимости пути v-t с использованием не более i ребер. Согласно (6.22), исходная задача заключается в вычислении OPT(n - 1, s). (Также алгоритм можно спроектировать так, чтобы подзадачи соответствовали минимальной стоимости пути s-v, использующего не более i ребер. Такая форма образует более естественную параллель с алгоритмом Дейкстры, но она не столь естественна в контексте протоколов маршрутизации, о которых речь пойдет позднее.)

Теперь нужно найти простой способ выражения OPT(i, v) с использованием меньших подзадач. Как вы увидите, в наиболее естественном решении задействовано много разных параметров; это еще один пример принципа “многовариантного выбора”, представленного в алгоритме сегментированной задачи наименьших квадратов.

Зафиксируем оптимальный путь P, представляющий OPT(i, v) на рис. 6.22.

♦ Если путь P содержит не более i - 1 ребер, то OPT(i, v) = OPT(I - 1, v).

♦ Если путь P содержит i ребер и первым является ребро (v, w), то OPT(i, v) = cvw + OPT(i - 1, w).

Так мы приходим к следующей рекурсивной формуле.

(6.23) Если i > 0, TO

Используя это рекуррентное соотношение, получаем следующий алгоритм динамического программирования для вычисления значения OPT(n - 1, s).

Правильность метода доказывается индукцией напрямую из (6.23). Время выполнения можно ограничить следующим образом: таблица M состоит из n² элементов; на вычисление каждого элемента может потребоваться время O(n), так как нам придется рассмотреть максимум n узлов w ∈ V. ■

(6.24) Метод кратчайшего пути правильно вычисляет минимальную стоимость пути s-t в графе, не содержащем отрицательных циклов, и выполняется за время O(n³).

Для таблицы M, шдержащей оптимальные значения подзадач, кратчайший путь, содержащий не более i ребер, может быть получен за время O(in) посредством обратного отслеживания по меньшим подзадачам.

В качестве примера рассмотрим граф на рис. 6.23, а, в котором требуется найти кратчайший путь от каждого узла до t. В таблице на рис. 6.23, b представлен массив M, элементы которого соответствуют значениям M [i, v] из алгоритма. Одна строка таблицы соответствует кратчайшему пути из конкретного узла в t, так как количество ребер в пути может увеличиться. Например, кратчайший путь из узла d в t обновляется четыре раза: из d-t в d-a-t, d-a-b-e-t и, наконец, d-a-b-e-c-t.

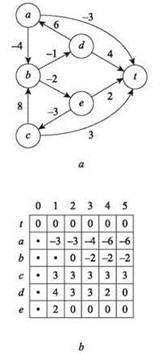
Рис. 6.23. Для направленного графа в (а) алгоритм кратчайшего пути строит таблицу динамического программирования (b)

Расширения: основные усовершенствования алгоритма

Анализ улучшенного времени выполнения

Как выясняется, мы можем обеспечить более точный анализ времени выполнения для случая, если граф G содержит не слишком много ребер. Направленный граф с n узлами может иметь примерно до n² ребер, так как теоретически ребро может связывать каждую пару узлов, но многие графы оказываются намного более разреженными. Как мы уже неоднократно видели в примерах, при работе с графом, у которого количество ребер m значительно меньше n², время выполнения может быть полезно записывать формулой, содержащей как m, так и n; это позволит ускорить обработку для графов с относительно небольшим количеством ребер.

Если действовать чуть внимательнее при анализе приведенного выше метода, можно улучшить время выполнения до O(mn) без значительного изменения самого алгоритма.

(6.25) Метод кратчайшего пути может быть реализован за время O(mn).

Доказательство. Рассмотрим вычисление элемента массива M[i, v] в соответствии с рекуррентным отношением (6.23); имеем

Мы предположили, что вычисление этого минимума может занять время до O(n), так как существуют n возможных узлов w. Но разумеется, этот минимум необходимо вычислять только по узлам w, с которым узел v связан ребром; обозначим это число n_v. В этом случае вычисление элемента массиваM[i, v] занимает время O(n_v). Элемент должен вычисляться для каждого узла v и каждого индекса 0 ≤ i ≤ n - 1, поэтому в результате получается время выполнения

В главе 3 точно такой же анализ проводился для других алгоритмов, работающих с графами, а утверждение (3.9) из этой главы использовалось для ограничения выражения для ненаправленных графов. Здесь мы имеем дело с направленными графами, а n_v обозначает количество ребер, выходящих из v. В некотором смысле работать со значением для направленных графов даже проще: каждое ребро выходит ровно из одного узла V, поэтому каждое ребро учитывается в этом выражении ровно один раз. Следовательно, имеем Подставляя этот результат в выражение

для времени выполнения, получаем границу времени выполнения O(mn). ■

Снижение затрат памяти

Всего одно небольшое изменение реализации позволит значительно снизить затраты памяти. Типичным недостатком многих алгоритмов динамического программирования являются высокие требования к памяти, обусловленные необходимостью хранения массива M. В алгоритме Беллмана-Форда в том виде, в каком он записан, этот массив имеет размер n²; тем не менее сейчас мы покажем, как сократить его до O(n). Вместо того чтобы сохранять M[i, v] для каждого значения i, мы будем использовать и обновлять одно значение M[v] для каждого узла v — длину кратчайшего пути из v в t, найденного на данный момент. Алгоритм, как и прежде, выполняется для итераций i = 1, 2, ..., n - 1, но i теперь используется как простой счетчик; при каждой итерации и для каждого узла v выполняется обновление

А теперь отметим следующий факт.

(6.26) На протяжении работы алгоритма M[v] содержит длину некоторого пути из v в t и после i циклов обновлений значение M[v] не превышает длину кратчайшего пути из v в t, использующего не более i ребер.

С учетом (6.26) мы теперь снова можем использовать (6.22), чтобы показать, что работа завершена после n - 1 итераций. Так как сохраняется только массив M, индексируемый по узлам, для его хранения достаточно памяти O(n).

Поиск кратчайших путей

Одна из проблем, о которой стоит помнить, — содержит ли версия алгоритма, эффективная по затратам памяти, достаточно информации для восстановления самих кратчайших путей? В случае алгоритма выравнивания последовательностей из предыдущего раздела нам пришлось прибегнуть к хитроумному методу “разделяй и властвуй” для восстановления решения в реализации, эффективной по затратам памяти. Однако на этот раз короткие пути восстанавливаются намного проще.

Чтобы облегчить восстановление кратчайших путей, мы усовершенствуем код: каждый узел v будет сохранять первый узел (после себя) на пути к конечной точке t; обозначим этот первый узел first[v]. Значение first[v] обновляется при каждом обновлении расстояния M[v], Другими словами, когда значение М[v] сбрасывается до минимума мы присваиваем first[v] узел w, для которого этот минимум достигается.

Пусть теперь P обозначает направленный “граф указателей”, узлами которого являются V, а ребрами — {(v,first[v])}. Ключевой факт заключается в следующем:

(6.27) Если граф указателей P содержит цикл C, то этот цикл должен иметь отрицательную стоимость.

Доказательство. Если first[v] = w в любой момент времени, то должно выполняться условие M[v] > c_vw + M[w]. В самом деле, левая и правая стороны равны после обновления, которое задает first[v] равным w; а поскольку M[w] может уменьшаться, это уравнение может превратиться в неравенство.

Пусть v₁, v₂, ..., v_k — узлы, входящие в цикл C графа указателей; будем считать, что (v_k, v₁) — последнее добавляемое ребро. Теперь рассмотрим значения непосредственно перед последним обновлением. В этот момент для всех i = 1, ..., k - 1, а также потому что мы собираемся обновить M[v_k] и изменить first[v_k] на v₁. При суммировании всех этих неравенств значения M[v_i] аннулируются, и мы получаем отрицательный цикл, как и утверждалось. ■

Теперь заметим, что если G не содержит отрицательных циклов, то из (6.27) следует, что в графе указателей P никогда не будет циклов. Для узла v рассмотрим путь, получаемый переходами по ребрам P: от v к first[v] = v₁, затем first[v₁] = v₂, и т. д. Так как граф указателей не содержит циклов, а приемник t — единственный узел, не имеющий исходящего ребра, этот путь должен вести к t. Утверждается, что при завершении алгоритма он действительно будет кратчайшим путем из v в t для графа G.

Доказательство. Рассмотрим узел v; пусть w = first[v]. Так как алгоритм завершился, должно выполняться условие M[v] = c_vw + M[w]. Значение M[t] = 0, а следовательно, длина пути, отслеживаемого по графу указателей, равна точно M[v] — что, как мы знаем, является расстоянием кратчайшего пути.

Обратите внимание: в версии алгоритма Беллмана-Форда, более эффективной по затратам памяти, количество ребер в пути, длина которого равна M[v] после i итераций, может существенно превышать i. Например, если граф представляет собой единственный путь из s в t и обновления выполняются в порядке, обратном порядку следования ребер в пути, окончательные значения кратчайшего пути будут получены всего за одну итерацию. Такое происходит не всегда, поэтому говорить об улучшении времени выполнения худшего случая не приходится, но было бы неплохо воспользоваться этим фактом для ускорения алгоритма в тех экземплярах, где это все же происходит. Для этого в алгоритме нужно предусмотреть “стоп-сигнал” — некий признак, который сообщит о возможности безопасного завершения перед достижением итерации n - 1.

Таким “стоп-сигналом” является простая последовательность следующих наблюдений: если когда-либо будет выполнена полная итерация i, в которой не изменится ни одно значение M[v], то ни одно значение M[v] не изменится в будущем, потому что будущие итерации будут начинаться с тем же набором элементов массива. Следовательно, выполнение алгоритма может быть безопасно прервано. Обратите внимание: если отдельное значение M[v] остается неизменным, этого недостаточно; для безопасного завершения все эти значения должны остаться неизменными в течение одной итерации. ■