Измерение количества информации - Информация. Измерение информации. Кодирование информации

Конспект

Вероятностный подход к измерению количества информации. Информация как снятая неопределённость в знаниях

Для определения количества информации, содержащейся в сообщении о каком-либо объекте или событии, используется вероятностный подход. Он основан на следующих соображениях:

• те или иные события имеют некоторую вероятность (возможность произойти или не произойти);

• событие, которое совершается всегда, имеет вероятность, равную 1 (например, восход Солнца); событие, которое не совершается никогда, имеет вероятность, равную 0 (например, восход Солнца на западе); в остальных случаях вероятность совершения события есть дробное число от 0 до 1;

• получая сообщение о совершении (или несовершении) некоторого события, мы получаем некоторое количество информации, которое определяется снятой с её помощью неопределённостью наших знаний об указанном событии:

- если вероятность совершения события точно равна 1 или 0 (т.е. мы точно знаем, что событие произойдёт (или не произойдёт), то никакой неопределённости в наших знаниях нет, и сообщение о таком событии несёт нулевое количество информации;

- для равновероятных событий чем больше их количество (т.е. шире возможный выбор вариантов и потому меньше вероятность каждого из них), тем большее количество информации несёт сообщение о совершившемся конкретном событии;

- количество информации в сообщении о совершении (несовершении) нескольких независимых событий равно сумме количеств информации, содержащейся в сообщениях о каждом отдельном таком событии.

Формула Хартли

Для N равновероятных возможных событий количество информации, которое несёт сообщение о выборе (совершении) одного конкретного события, определяется формулой Хартли:

где log — функция логарифма по основанию 2, обратная возведению значения основания логарифма в степень, равную I, т.е. из формулы Хартли следует зависимость:

Для облегчения вычислений для значений N, представляющих собой степени числа 2, можно составить таблицу (табл. 1.1):

Таблица 1.1

N	2	4	8	16	32	64	128	256	512	1024
I (бит)	1	2	3	4	5	6	7	8	9	10

Для значений N, не равных степени двойки, при определении количества информации в битах из вышеприведённой таблицы берётся ближайшее большее значение N, равное степени 2. Например, для 48 равновозможных событий количество информации, которое содержится в сообщении о совершении конкретного события, принимается равным 6 бит (так как ближайшее большее значение N, равное степени числа 2, равно 64).

“Принцип вилки”

Для приближённого вычисления количества информации при значении N, не равном 2 в некоторой степени, определяются значения количества информации для двух соседних значений N, составляющих степени 2, и составляется соответствующее двойное неравенство.

Например, пусть нужно оценить количество информации в сообщении о выпадении на верхней грани игрального кубика шести точек. В этом случае N = 6. Ближайшими к нему являются значения — степени двойки: N = 4 (2 ∙ 2) и N = 8 (2 ∙ 2 ∙ 2). Тогда можно составить неравенство:

Отсюда искомое количество информации будет больше 2 и меньше 3 битов.

Формула Шеннона. Связь количества информации с понятием вероятностей

Для N событий с различными вероятностями p₁, р₂, ..., p_N количество информации определяется формулой Шеннона:

Если все эти события равновероятны, т. е. р₁ = р₂ = ... = p_N = p, то очевидно, что формула Шеннона преобразуется в формулу Хартли (которая, таким образом, представляет собой частный случай формулы Шеннона).

Связь между количеством информации и вероятностью события

Для N равновероятных событий вероятность одного отдельного события р = 1/N. С учётом этого формула Хартли может быть преобразована в соотношение:

В этом случае вычисление количества информации можно производить по табл. 1.1, предварительно вычислив значение N как величину, обратную значению р. Например, для события, вероятность которого (р) составляет 0,018, получается N = 1/0,018 = 55,56, тогда берётся ближайшее большее значение N, кратное 2 (N = 64) и по табл. 1.1 определяется, что I = 6 бит.

“Принцип ёлочки”

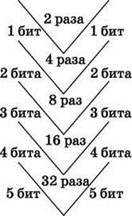
Сколько информации несёт в себе некоторое сообщение? Известно, что количество информации, равное 1 биту, соответствует снятию неопределённости при помощи ответа “да” или “нет” на один элементарный вопрос, т. е. 1 бит соответствует уменьшению неопределённости в 2 раза. А чему соответствует уменьшение неопределённости, например, в 4 раза? В подобном случае можно задать последовательно два вопроса, на которые даются ответы “да” или “нет”. В общем, количество информации в п бит позволяет уменьшить неопределённость в 2ⁿ раз.

Бит. Байт. Производные величины

Принято считать, что минимально возможное количество информации соответствует такому сообщению, получение которого уменьшает неопределённость в 2 раза (пример — сообщение о выпадении на подброшенной монете “орла” из двух равновозможных вариантов — “орёл” и “решка”). Это минимальное количество информации получило название “бит” (англ. bit как сокращение названия binary digit — двоичная цифра).

В вычислительной технике бит соответствует одному двоичному разряду, который может принимать одно из двух возможных значений: 0 или 1. В качестве более крупной величины принят байт, соответствующий двоичному числу из 8 разрядов (битов). В оперативной памяти компьютера минимальный объём ячейки памяти, выделяемой для хранения какой-либо величины, как правило, равен одному байту. Ячейки большего размера имеют объём, кратный байту с коэффициентом кратности 2: 2 байта (16 бит), 4 байта (32 бита), 8 байтов (64 бита). Такую “порцию” информации принято называть машинным словом.

В теории информации количество информации может быть дробной величиной. В вычислительной технике количество информации может составлять только целое число битов (дробное значение при необходимости округляется в большую сторону).

В вычислительной технике в большинстве практических задач получаемое количество битов округляется в большую сторону до целого количества байтов, хотя в некоторых случаях возможна “потоковая” запись значений, состоящих из количества битов, не кратного 8.

Для обозначения количеств информации, больших, чем байт, приняты следующие производные величины:

1 килобайт (КБ) = (2¹⁰ = 1024) байт;

1 Мегабайт (МБ) = (2¹⁰ = 1024) килобайт = (2²⁰ = 1048576) байт;

1 Гигабайт (ГБ) = (2¹⁰ = 1024) Мегабайт = (2²⁰ = 1048576) килобайт = (2³⁰ = 1073741824) байт;

1 Терабайт (ТБ) = (2¹⁰ = 1024) Гигабайт = (2²⁰ = 1048576) Мегабайт = (2³⁰ = 1073741824) килобайт = (2⁴⁰ = 1099511627776) байт;

1 Петабайт (ПБ) = (2¹⁰ = 1024) Терабайт;

1 Эксабайт (ЭБ) = (2¹⁰ = 1024) Петабайт;

1 Зеттабайт (ЗБ) = (2¹⁰ = 1024) Эксабайт;

1 Йоттабайт (ЙБ) = (2¹⁰ = 1024) Зеттабайт.

Внимание! В отличие от одноименных приставок в кратных величинах в математике изменение величин в вычислительной технике происходит на каждом “шаге” вышеуказанной шкалы на 2¹⁰= 1024, а не на 10³ = 1000.

Для избежания этой путаницы были предложены особые, двоичные приставки для производных величин количества информации:

Кибибайт	KiB	210 (1024)
Мебибайт	MiB	220 (1048576)
Гибибайт	GiB	230 (1073741824)
Тебибайт	TiB	240 (1099511627776)
Пебибайт	PiB	250 (1125899906842624)
Эксбибайт	EiB	260 (1152921504606846976)

Алфавитный (алгоритмический) подход к измерению количества информации. Алфавит. Мощность алфавита

В этом случае количество информации в сообщении представляет собой чисто технический параметр (важный с точки зрения хранения или передачи информации) и не зависит от содержания сообщения.

При алфавитном подходе информационное сообщение рассматривается как некоторое количество (К) знаков (символов, кодов) из некоторого используемого полного набора, называемого алфавитом. Количество (N) знаков в алфавите называется мощностью этого алфавита.

В данном конкретном сообщении не обязательно используются все знаки алфавита. Мощность алфавита определяется не набором знаков, используемых в конкретном сообщении, а количеством знаков, которые вообще могут быть использованы в сообщениях, кодируемых в соответствии с данным алфавитом.

Алгоритм определения количества информации в сообщении:

1) определяется мощность используемого алфавита N;

2) определяется количество информации, приходящееся в алфавите на один его знак:

• если использование всех знаков равновероятно, то используется формула Хартли (либо её следствие: N = 2^I) и табл. 1.1;

• если известны вероятности использования тех или иных знаков (на основе составленной таблицы частоты встречаемости этих знаков), то используется формула Шеннона;

3) вычисленное количество информации (I), приходящееся на один знак, умножается на количество (К) знаков в данном сообщении:

Количество различных состояний панели, имеющей М элементов, каждый из которых может находиться в N различных состояниях, равно количеству различных М-разрядных чисел (начиная с нуля) в системе счисления с основанием N и вычисляется как N^M.

Количество всех М-разрядных чисел в системе счисления с основанием N равно N^M. Максимальное значение М-разрядного числа в системе счисления с основанием N равно (N^M - 1).

Если в условии задачи предлагается определить количество сигналов, подаваемых с помощью разного количества элементов (от X до Y), то нужно отдельно вычислить количества возможных сигналов для каждого возможного числа элементов и просуммировать полученные значения.

Разбор типовых задач

Задача 1.

Для регистрации на сайте некоторой страны пользователю требуется придумать пароль. Длина пароля — ровно 11 символов. В качестве символов используются десятичные цифры и 12 различных букв местного алфавита, причём все буквы используются в двух начертаниях: как строчные, так и заглавные (регистр буквы имеет значение!).

Под хранение каждого такого пароля на компьютере отводится минимально возможное и одинаковое целое количество байтов, при этом используется посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством битов.

Определите объём памяти в байтах, который занимает хранение 60 паролей.

Решение

Данная задача решается с использованием алфавитного подхода к измерению количества информации.

1. Определяется мощность используемого алфавита. Используются десятичные цифры (10 различных знаков) и 12 букв, каждая из которых может иметь два возможных начертания (12 х 2 = 24 различных знака). Итого мощность используемого алфавита составляет: 10 + 12 х 2 = 34 знака.

2. Исходя из известной мощности алфавита определяется количество битов, соответствующее каждому знаку. N = 34. Речь идёт о целом (не дробном!) количестве битов, минимально достаточном для представления одного знака такого алфавита. Поэтому выбирается ближайшее большее число N, равное степени числа 2: N = 2⁶ = 64 (значения 2⁵ = 32 недостаточно). Тогда согласно формуле N = 2^I получается: I = 6 бит на один знак алфавита.

3. Длина пароля (длина сообщения, кодируемого с использованием рассмотренного алфавита) равна 11 символам (К = 11). Тогда согласно формуле I_∑ = I ∙ К, количество информации в битах, соответствующее всему такому сообщению (паролю), равно 6 ∙ 11 = 66 битов.

4. По условию задачи, под хранение каждого такого пароля на компьютере отводится минимально возможное и одинаковое целое количество байтов. Определяется минимальное количество целых байтов, достаточное, чтобы уместить 66 битов. 1 байт равен 8 битам. Выполняем деление количества битов (66) на 8 с округлением результата до целого в большую сторону: 66 / 8 = 8,25 → 9 байтов.

Следует не забывать выполнять перевод количества битов в количество байтов!

5. Тогда для хранения 60 паролей потребуется 60 ∙ 9 = 540 байтов.

Ответ: 540 байтов.

Задача 2.

В некоторой стране автомобильный номер длиной 7 символов составляют из заглавных букв (используются только 22 различные буквы) и десятичных цифр в любом порядке. Каждый такой номер в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит).

Определите объём памяти в байтах, отводимый этой программой для записи 50 номеров.

Решение

1. Определяется мощность используемого алфавита. Используются десятичные цифры (10 различных знаков) и 22 буквы (только заглавные). Мощность используемого алфавита составляет: 10 + 22 = 32 знака.

2. Исходя из известной мощности алфавита, определяется количество битов, соответствующее каждому знаку. N = 32. Ему соответствует значение 2⁵ = 32. Тогда согласно формуле N = 2^Iполучается: I = 5 бит на один знак алфавита.

3. Длина автомобильного номера (длина сообщения, кодируемого с использованием рассмотренного алфавита) равна 7 символам (К = 7). Согласно формуле I_∑ = I ∙ К, количество информации вбитах, соответствующее всему такому сообщению (номеру), равна 5 ∙ 7 = 35 битов.

4. По условию задачи, под хранение каждого такого номера на компьютере отводится минимально возможное и одинаковое целое количество байтов. Определяется минимальное количество целых байтов, достаточное, чтобы уместить 35 битов. 1 байт равен 8 битам. Выполняется деление количества битов (35) на 8 с округлением результата до целого в большую сторону: 35 / 8 = 4,375 → 5 байтов.

5. Тогда для хранения 50 номеров потребуется 50 ∙ 5 = 250 байтов.

Ответ: 250 байтов.

Задача 3.

В школьной компьютерной сети каждому учащемуся выдаётся пароль, состоящий из 15 восьмеричных цифр. При этом символы кодируют одинаковым минимально возможным количеством битов. В базе данных, в которой хранятся сведения о паролях, для каждого пользователя отводится одинаковое минимально возможное целое количество байтов. Кроме самого пароля, для каждого пользователя в базе данных также хранится дополнительная информация, занимающая целое количество байтов (одинаковое для всех пользователей). Для хранения сведений о 20 учащихся потребовалось 320 байтов.

Сколько байтов занимает дополнительная информация об одном пользователе? (В ответе нужно указать только целое число — количество байтов.)

Решение

Данная задача аналогична предыдущей. Отличие заключается только в наличии в записи о пользователе дополнительных байтов (количество которых и нужно найти).

1. Алфавит состоит из 8 символов (восемь восьмеричных цифр от 0 до 7). Следовательно, для хранения одного такого символа достаточно 3 бита (2³ = 8).

2. В пароле содержится 15 символов, тогда для хранения собственно пароля требуется 15 ∙ 3 = 45 битов.

3. На 20 пользователей требуется 320 байтов. Значит, на одного пользователя отводится 320/20 = 16 байтов.

4. Дополнительная информация занимает целое количество байтов. Тогда на собственно пароль тоже должно отводиться минимально возможное количество целых байтов — а именно, 6 байтов (6 ∙ 8 = 48 битов, а 5 ∙ 8 = 40 битов — слишком мало).

5. Тогда получим уравнение: 16 = 6 + X, откуда X = 10 байтов отводится на дополнительную информацию.

Ответ: 10.

Задача 4.

Для передачи сигналов на флоте используются специальные сигнальные флаги, вывешиваемые в одну линию (последовательность важна). Какое количество различных сигналов может передать корабль при помощи четырёх сигнальных флагов, если на корабле имеются флаги трёх различных видов (флагов каждого вида неограниченное количество).

Решение

1. Имеются флаги трёх возможных видов, — следовательно, это аналог троичной системы счисления.

2. Всего последовательность флагов содержит четыре флага, значит, она является аналогом четырёхзначного троичного числа.

3. Количество различных сигналов, которые можно подавать при помощи такого набора флагов, равно количеству всех возможных значений троичных чисел от 0000 до 2222 включительно, т.е. 3⁴ = 81 сигнал.

Если имеется М элементов, каждый из которых может находиться в N различных состояниях (либо быть одним из N различных видов), то количество состояний такой системы (передаваемых с её помощью сообщений) равно количеству различных М-разрядных чисел (начиная с нуля) в системе счисления с основанием N и вычисляется как N^M.

Ответ: 81 сигнал.

Задача 5.

Некоторое сигнальное устройство за одну секунду передает один из трёх сигналов. Сколько различных сообщений длиной в четыре секунды можно передать при помощи этого устройства?

Решение

1. Возможна передача одного из трёх односекундных сигналов — следовательно, это аналог троичной системы счисления.

2. Длина сообщения составляет 4 секунды, значит, это аналог четырёхзначного троичного числа.

3. Количество различных таких сигналов равно количеству всех возможных значений четырёхзначных троичных чисел (от 0000 до 2222 включительно), т.е. 3⁴ = 81 сообщение.

Количество различных сообщений, включающих в себя М элементов, каждый из которых может иметь N различных состояний, равно количеству различных М-разрядных чисел (начиная с нуля) в системе счисления с основанием N и вычисляется как N^M.

Ответ: 81 сообщение.