Равномерные и неравномерные двоичные коды - Информация. Измерение информации. Кодирование информации

Конспект

Равномерные и неравномерные двоичные коды. Условие Фано

Кодирование символов обычно предполагает, что каждому символу всегда сопоставляется одинаковое количество битов (например, в кодовой таблице ASCII каждому символу сопоставляется один байт, хранящий порядковый номер того или иного символа в этой таблице). Такой способ кодирования прост и удобен, однако очевидно, что он является не самым оптимальным. Для значительной части символов используются не все биты отведенных под них байтов (часть старших битов — нулевые), а при наличии в тексте только части символов, предусмотренных в таблице ASCII (например, если текст содержит только прописные русские буквы), приходится все равно использовать 8-битный код.

Более компактным является неравномерный двоичный код (особенно если при его построении исходить из частоты встречаемости различных символов и присваивать наиболее часто используемым знакам самые короткие коды, как это сделано в методе Хаффмана). При этом количество битов, отводимых для кодирования символов, в целом зависит от количества используемых в конкретном случае различных символов (от мощности алфавита), а коды, соответствующие разным символам, могут иметь различную длину в битах.

Главное при таком кодировании — обеспечить возможность однозначного декодирования записанной с помощью этих кодов строки (поочередного, слева направо, выделения и распознавания из сплошной последовательности нулей и единиц кодов отдельных букв). Для этого коды символам необходимо назначать в соответствии с условиями Фано.

Прямое условие Фано. Неравномерный код может быть однозначно декодирован, если никакой из кодов не совпадает с началом (префиксом) какого-либо другого, более длинного кода.

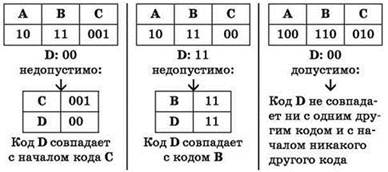
Обратное условие Фано. Неравномерный код может быть однозначно декодирован, если никакой из кодов не совпадает с окончанием (постфиксом) какого-либо другого, более длинного кода.

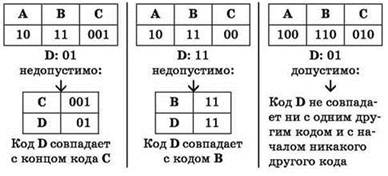
Для однозначности декодирования последовательности кодов достаточно выполнения хотя бы одного из двух вышеуказанных условий Фано:

— при выполнении прямого условия Фано последовательность кодов однозначно декодируется с начала;

— при выполнении обратного условия Фано последовательность кодов однозначно декодируется с конца.

Выбрать, какое из двух правил Фано используется при решении конкретной задачи, можно, проанализировав коды в условии задачи (без учёта кода, проверяемого в вариантах ответа): если для исходных кодов выполняется прямое правило Фано, то его и нужно использовать при решении, и наоборот.

Вместе с тем нужно помнить, что правила Фано — это достаточное, но не необходимое условие однозначного декодирования: если не выполняется ни прямое, ни обратное правило Фано, конкретная двоичная последовательность может оказаться такой, что она декодируется однозначно (так как остальные возможные варианты до конца декодирования довести не удаётся). В подобном случае необходимо пытаться строить дерево декодирования в обоих направлениях.

Рекомендуется начинать решение задач такого типа с анализа выполнимости правил Фано для исходных кодов, указанных в условии задачи (т.е. без учета искомого кода в вариантах ответов). В зависимости от того, какое из двух правил Фано выполняется для исходных кодов, при дальнейшем решении задачи производится сравнение более короткого кода с началом (при выполнении прямого правила Фано) или с концом (при выполнении обратного правила Фано) более длинного кода.

Если для заданной последовательности кодов выполняется прямое правило Фано, то её декодирование необходимо вести с начала (слева направо).

Если для заданной последовательности кодов выполняется обратное правило Фано, то её декодирование необходимо вести с конца (справа налево).

При сравнении пары кодов удобно подписывать более короткий код под более длинным, выравнивая эти записи по левому краю — для прямого правила Фано либо по правому краю — для обратного правила Фано.

Разбор типовых задач

Задача 1.

Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, решили использовать неравномерный двоичный код, позволяющий однозначно декодировать двоичную последовательность, появляющуюся на приёмной стороне канала связи. Использовали код: А-1, Б-000, В-001, Г-011. Укажите, каким кодовым словом должна быть закодирована буква Д. Длина этого кодового слова должна быть наименьшей из всех возможных. Код должен удовлетворять свойству однозначного декодирования.

1) 00

2) 01

3) 11

4) 010

Решение

Проверяемый код буквы Д	Существующие коды букв А, Б, В и Г				Вывод
	А	Б	В	Г
	1	000	001	011
00	00 1 Совпадения нет	000 00 Совпадение есть!	001 00 Совпадение есть!	011 00 Совпадения нет	Код 00 для буквы Д непригоден
01	01 1 Совпадения нет	000 01 Совпадения нет	001 01 Совпадения нет	011 01 Совпадение есть!	Код 01 для буквы Д непригоден
11	11 1 Совпадение есть!	000 11 Совпадения нет	001 11 Совпадения нет	011 11 Совпадения нет	Код 11 для буквы Д непригоден
010	010 1 Совпадения нет	000 010 Коды не равны	001 010 Коды не равны	011 010 Коды не равны	Код 010 для буквы Д пригоден

В итоге, допустимым для буквы Д является код 010. Это единственный возможный вариант, поэтому условие о том, что кодовое слово должно иметь минимально возможную длину, в данном случае не требуется.

Ответ: код 010 (вариант №4).

Задача 2.

Для кодирования последовательности символов, состоящей из букв К, И, Н, О, используется неравномерный двоичный код, удовлетворяющий условию Фано. При этом для буквы К использован код 0, а для буквы И — код 11. Требуется определить наименьшую возможную суммарную длину всех кодовых слов указанных букв.

1) 8

2) 9

3) 10

4) 11

Решение

Для проверки на соответствие кодов условию Фано нужно попарно сравнивать между собой коды по следующим правилам:

• когда длина обоих сравниваемых кодов совпадает, проверяется равенство этих кодов: если один код совпадает с другим, то такая пара кодов неправильна (не удовлетворяет условию Фано);

• когда длина сравниваемых кодов различна, более короткий код записывается под более длинным с выравниванием обоих кодов по левому краю: если все знаки более короткого кода совпадают с соответствующими знаками в начале более длинного кода, то такая пара кодов неправильна (не удовлетворяет условию Фано).

Опираясь на эти правила, подбираются коды для оставшихся букв Н и О. Начнём с буквы Н и будем перебирать возможные двоичные числа с возрастающей длиной (важно получить наименьшую возможную суммарную длину кодов!).

Код буквы К	Код буквы И	Предполагаемый код буквы Н	Комментарий
0	11	1	Нельзя, так как совпадает с началом кода буквы И
		00	Нельзя — код буквы К совпадает с его началом
		01	Нельзя — код буквы К совпадает с его началом
		10	Допустимый код (не совпадает с двузначным кодом буквы И, а код буквы К не совпадает с его началом)

Итак, можно предположить, что первый код найден. Но посмотрим — удастся ли при этом найти код для оставшейся четвёртой буквы О. При этом можно сразу отбросить те коды, которые не подошли для буквы Н, — ведь код буквы О должен удовлетворять тем же требованиям при сравнении с кодами букв К и И.

Код буквы К	Код буквы И	Код буквы Н	Предполагаемый код буквы О	Комментарий
0	11	10	11	Нельзя — совпадает с кодом буквы И
			000, 001, 010, 011	Нельзя — код буквы К совпадает с его началом
			100, 101	Нельзя — код буквы Н совпадает с его началом
			110, 111	Нельзя — код буквы Н совпадает с его началом

Очевидно, и дальше с увеличением числа разрядов в предполагаемом коде буквы О будет сохраняться та же тенденция: ни один код не пригоден. Как же быть?

Причина этой прискорбной ситуации — в том, что, выбрав для буквы Н код 10, мы “закрыли” для себя возможность дальнейшего расширения нашей кодовой системы. Поэтому вместо кода 10 придётся выбрать для буквы Н более длинный код, — например, 100.

Теперь повторим попытку поиска кода для буквы О:

Код буквы К	Код буквы И	Код буквы Н	Предполагаемый код буквы О	Комментарий
0	11	100	101	Допустимый код (не совпадает с трёхзначным кодом буквы Н, а коды букв К и И не совпадают с его началом)

Таким образом, решение найдено. Выпишем коды всех четырёх букв:

К	И	Н	О
0	11	100	101

Подсчитаем суммарную длину этих кодов (в знаках): 1 + 2 + 3 + 3 = 9.

Ответ: 9 (вариант №2).

Задача 3.

При передаче информации используется равномерный двоичный код. Передаче подлежат сообщения, которые могут состоять только из четырёх букв: “И”, “Н”, “Ф”, “О”, при этом каждой букве соответствует отдельное кодовое слово.

Для используемого набора кодовых слов выполняется обязательное правило: любые два кодовых слова из этого набора должны различаться как минимум в трёх разрядах.

Для кодирования букв “И”, “Н”, “О” используются следующие 5-битовые кодовые слова:

“И”: 11110, “Н”: 10000, “О”: 01001. Про 5-битовый код для буквы “Ф” известно, что оно начинается с 0 и заканчивается 1.

Укажите кодовое слово для буквы “Ф”.

Решение

В задачах этого типа речь идёт об обычном двоичном коде, длина которого одинакова для всех кодируемых символов. Условия Фано в этом случае не используются, а для решения задачи достаточно обычных рассуждений.

1. По условию, любые два кодовых слова из используемого набора различаются как минимум в трёх разрядах. Запишем предполагаемый код буквы “Ф”, заменяя неизвестные пока биты звездочками: “Ф”: 0***1.

2. Сравним этот код с известными кодами других букв:

“И”: 11110

“Н”: 10000

“О”: 01001

“Ф”: 0***1

Видим, что начальный и конечный биты кода буквы “Ф” не совпадают с соответствующими битами кодов букв “И” и “Н”, но совпадают (причём оба!) с начальным и конечным битами для буквы “О”.

3. По условию, нужно, чтобы коды “О” и “Ф” различались как минимум в трёх позициях. А такое различие нам могут дать только три внутренних бита.

Тогда для “Ф” вместо звёздочек надо выбрать биты, противоположные соответствующим битам для “О”:

“О”: 01001

“Ф”: 00111

3. Для кодов “Ф” и “О” требуемое условие соблюдено. Проверим его соблюдение для кодов остальных букв:

“И”: 11110 “Н”: 10000

“Ф”: 00111 “Ф”: 00111

3 различия 4 различия

Таким образом, условие соблюдено и для этих кодов.

Ответ: 10110.