Задачи на графах - Моделирование и компьютерный эксперимент

Конспект

Граф — это один из способов графического представления информации, отражающий количество объектов изучаемой системы и взаимосвязи между ними.

Объекты, отраженные в графе, представлены в нём как вершины (узлы) графа, а связи между ними — как дуги (рёбра). Таким образом, граф представляет собой совокупность непустого множества вершин и множества связей между вершинами.

Количество вершин графа называют его порядком. Количество рёбер называют размером графа.

Рёбрам графа могут быть сопоставлены числовые значения, которые называют весами рёбер. Например, вес ребра в графе, обозначающем дорожную сеть, может представлять собой длину соответствующей дороги между вершинами графа, обозначающими населённые пункты. Граф, рёбрам которого назначены значения весов, называют взвешенным.

Две вершины называют концевыми вершинами (концами) ребра, которое их соединяет. При этом говорят, что ребро инцидентно каждой из соединяемых им вершин, и наоборот, каждая концевая вершина называется инцидентной соединяющему их ребру. Две концевые вершины одного и того же ребра называют соседними.

Рёбра, имеющие общую концевую вершину, называют смежными.

Рёбра, инцидентные одной и той же паре вершин (т.е. соединяющие одну и ту же пару вершин) называют кратными, или параллельными. Граф с кратными рёбрами называют мультиграфом.

Ребро, концами которого является одна и та же вершина, называется петлёй. Граф, содержащий петли (и кратные рёбра), называют псевдографом.

Степенью вершины называют количество инцидентных ей (исходящих из неё) рёбер, при этом петли, замкнутые на эту вершину, входят в подсчёт дважды.

Вершина называется изолированной, если она не является концом ни для одного ребра. Вершина называется висячей (листом), если она является концом ровно одного ребра.

Пустой граф — граф, состоящий из произвольного количества изолированных вершин (т.е. не имеющий рёбер).

Полный граф — граф, не имеющий петель и кратных рёбер, в котором каждая пара вершин соединена ребром.

Путь (цепь) в графе — конечная последовательность вершин, каждая из которых (кроме последней) соединена со следующей вершиной ребром. Циклом называют путь, в котором первая и последняя вершины совпадают. Путь (или цикл) называют простым, если рёбра в нём не повторяются. Простой путь (цикл) называют элементарным, если вершины в нём не повторяются.

Длиной пути (или цикла) называют количество составляющих его рёбер.

Связный граф — граф, в котором для любых двух вершин существует связывающий их путь.

Сильно связный граф — ориентированный граф, в котором существует маршрут из любой вершины в любую другую.

Неориентированный граф

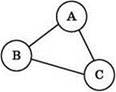
В неориентированном графе связи между любыми парами концевых вершин являются двунаправленными, т.е. эти концевые вершины “равноправны” по отношению к этой связи.

Пример неориентированного графа:

Ориентированный граф (орграф)

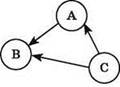
В ориентированном графе связи между концевыми вершинами являются направленными. Рёбра ориентированного графа называют дугами. Пути в ориентированном графе называют ориентированными путями (маршрутами). Замкнутый путь (цикл) в ориентированном графе называют контуром. Ориентированный граф, в котором каждая пара концевых вершин связана только одной дугой, называют направленным (в отличие от него, в простом ориентированном графе какие-то вершины могут быть соединены двумя дугами, имеющими противоположные направления). Полный направленный граф называют турниром. Ориентированный граф, полученный из исходного путём смены направлений рёбер на противоположные, называют обратным.

Пример ориентированного графа (является направленным, турниром):

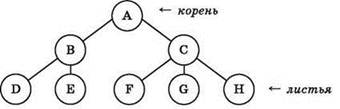
Дерево — граф, в котором существует один-единственный путь между любой парой вершин и не имеется ни одного цикла. Ориентированное (направленное) дерево — орграф, в котором существует один-единственный маршрут между любой парой вершин и не имеется ни одного контура. Одна из вершин дерева (его корень) не имеет входящих в нее дуг, а все остальные вершины имеют ровно одну входящую дугу. При этом вершины, не имеющие исходящих из них дуг, называются листьями. Пример дерева:

Двоичное дерево — ориентированное дерево, в котором для каждой вершины количество исходящих из неё дуг не превосходит двух.

Способы представления графов

1. Графический способ — изображение графа.

Пример:

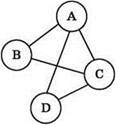
2. Список рёбер — перечисление всех рёбер графа как пар обозначений связываемых этими рёбрами вершин.

Пример: {А,В}, {A,D}, {А,С}, {В,С}, {C,D}

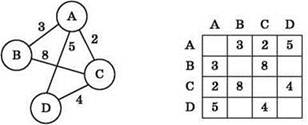
3. Матрица смежности — квадратная симметричная таблица (матрица), в которой и столбцы, и строки соответствуют вершинам графа, а в ячейках на их пересечении записываются числа, обозначающие наличие или отсутствие связей между соответствующими парами вершин (обычно — количество связей между вершинами).

В простейшем случае, когда граф не имеет кратных рёбер и петель, матрица смежности содержит единицы для ячеек, соответствующих парам вершин, связанных ребром, и нули — для несвязанных вершин.

Пример:

Для взвешенного графа возможен вариант матрицы смежности, где в ячейках записываются веса рёбер или нули (либо ячейки оставляются пустыми).

Пример:

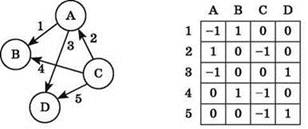
4. Матрица инцидентности — таблица, столбцы которой соответствуют вершинам, а строки — рёбрам. При этом в ячейках на их пересечении записываются числа:

— для неориентированного графа — число 1, если данная вершина инцидентна данному ребру, или 0 — в противном случае;

— для ориентированного графа — число -1, если данная дуга исходит из данной вершины, число 1, если данная дуга входит в данную вершину, число 2, если дуга представляет собой петлю, или 0 — в противном случае.

Пример:

Разбор типовых задач

Задача 1.

Между населёнными пунктами А, В, С, D, Е, F построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)

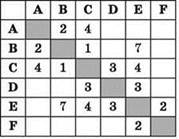
Определите длину кратчайшего пути между пунктами А и F (при условии, что передвигаться можно только по построенным дорогам).

1) 9

2) 10

3) 11

4) 12

Решение

Это типичная задача на построение графов по заданной матрице смежности. Вершинами искомого графа (карты городов) являются названия городов, обозначенные буквами от А до F, а рёбра определяются наличием в таблице чисел, указывающих веса этих рёбер.

Построение такого графа — первый шаг решения задачи. Для этого достаточно разметить точки А, В, С, D, E, F и соединить линиями те из них, для которых на пересечении строки и столбца таблицы имеется непустая ячейка. Число, находящееся в этой ячейке, нужно записать над соответствующим ребром.

Поскольку граф в данном случае не является ориентированным (в условии не указано, что можно двигаться по дорогам только в одном направлении, значит, возможно и встречное движение), его матрица смежности зеркально симметрична относительно главной диагонали (выделенной серым фоном ячеек). Поэтому, при рисовании графа достаточно просмотреть, например, только ячейки над главной диагональю.

Для данной таблицы (матрицы смежности) получается граф следующего вида:

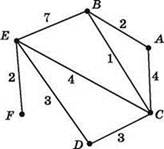
Остаётся перебрать все возможные пути от вершины А к вершине F. При этом обратить внимание, что любой такой путь заканчивается одинаково — отрезком EF:

ABEF — длина пути: 2 + 1 + 2 = 11;

ABCEF — длина пути: 2 + 1 + 4 + 2 = 9;

ACEF — длина пути: 4 + 4 + 2 = 10;

ABCDEF — длина пути: 2 + 1 + 3 + 3 + 2 = 11;

ACDEF — длина пути: 4 + 3 + 3 + 2 = 12.

Из них самый короткий — путь ABCEF длиной 9 единиц.

Ответ: 9 (вариант ответа №1).

Задача 2.

Между городами А, Б, В, Г, Д построены дороги, протяжённость которых указана в таблице. Отсутствие числа в ячейке означает, что прямой дороги между соответствующими городами нет.

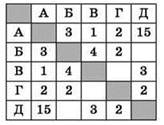
Найти длину кратчайшего пути между пунктами А и Д, проходящего через пункт В, если передвигаться можно только по указанным дорогам.

Решение

Как обычно, строим по таблице граф дорог:

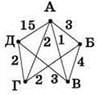
Дальше нужно искать все возможные пути из А в Д, отбрасывая те, которые не проходят через город В, подсчитывать их длину и искать путь с минимальным значением его суммарной длины.

Можно ли упростить и ускорить решение? Да! Можно сразу исключить из графа пути “в обход” города В:

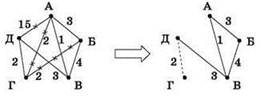
Получили совсем простой граф (тем более, что в город Г теперь вообще ни одна дорога из А не идёт, так что путь ГД тоже можно исключить).

В этом графе только два возможных пути:

• АБВД с длиной 3 + 4 + 3 = 10,

• АВД с длиной 1 + 3 = 4.

Причём то, что кратчайший из них — это путь АВД, — видно “невооруженным глазом”. Его длина 4 — и есть ответ.

Ответ: 4.

Задача 3.

Между населёнными пунктами А, В, С, D, Е, F, Z построены дороги с односторонним движением. В таблице указана протяжённость каждой дороги. Отсутствие числа в таблице означает, что прямой дороги между пунктами нет. Например, из А в В есть дорога длиной 4 км, а из В в А дороги нет.

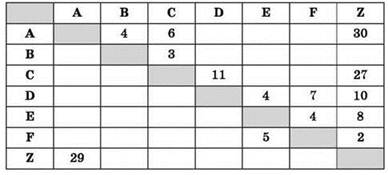
Сколько существует таких маршрутов из А в Z, которые проходят через 6 и более населённых пунктов? Пункты А и Z при подсчете учитывать. Два раза проходить через один пункт нельзя.

Решение

Речь идёт о построении графа по заданной табличной форме, но графа ориентированного, в котором рёбра обладают направлениями. Их нужно обозначать не отрезками, а стрелками. В случае же, если в таблице заданы и прямой, и обратный путь (как между пунктами А и Z), надо их изобразить двумя отдельными соответствующими стрелками. (Если бы в задаче требовалось определить длину пути, каждая стрелка должна была бы изображаться со своим весом — обозначением длины пути.) Точки (вершины графа) располагаем произвольно, не учитывая реальное их расположение, т.е. граф отражает лишь условную “карту дорог”.

1) Строим требуемый граф:

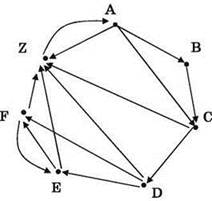
2) Начинаем подсчитывать пути. При этом помним, что через один и тот же пункт в пределах одного какого- то пути нельзя проходить дважды. (Можно при решении задачи на бумаге прорисовывать каждый путь своим цветом при помощи фломастера.) Например:

— AZ: путь напрямую из пункта А в пункт Z существует, но проходит только через два пункта, а не через 6 и более, — значит, он нам не подходит. (Обратный путь из Z в А вообще не учитываем, так как по условию задачи ищутся только пути из А в Z.)

— ABCDEFZ: путь через все вершины графа — он подходит, так как проходит через 7 вершин и ни одна из них не посещается дважды.

Аналогичным способом просматриваем остальные пути и выбираем среди них нужные.

Сложно? Есть риск что-то пропустить? Вспомним тогда задачу, где по ориентированному графу требовалось определить количество всех путей из одного города в другой. Ведь, по сути, это та же самая задача!

3) Рисуем дерево всех возможных путей из А в Z, при этом конечные точки маршрута (Z) выделяем цветом и рамкой. При этом важно не забыть о запрете на повторное посещение вершин. Это означает, что обратный путь FE нельзя рисовать в тех ветвях дерева, где уже где-то ранее фигурировали буквы Е и F (такие ветви в графе, где из Е допускается только один путь в Z, отметим пунктирными стрелками):

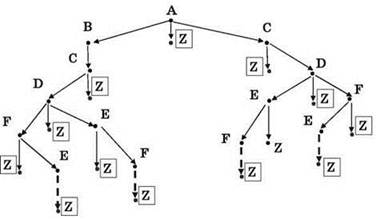
4) Остаётся подсчитать количество ветвей в этом графе, включающих в себя 6 и более вершин (т.е. когда запись последовательности имён проходимых вершин состоит из 6 и более букв). Это ветви (пути): ABCDFZ, ABCDFEZ, ABCDEZ, ABCDEFZ, ACDFEZ, ACDEFZ. Всего — 6 путей.

Построение дерева вариантов — это универсальный метод решения задач с перебором возможных вариантов (действий, решений, ходов и пр.), обладающий высокой наглядностью и существенно уменьшающий риск пропуска возможных вариантов. Однако данную задачу можно решить и более быстрым способом, сразу подсчитывая количества возможных путей в каждом узле.

Ответ: 6.

Задача 4.

Дана схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л, М. По каждой дороге можно двигаться только в направлении, указанном стрелкой. Сколько возможно различных путей из города А в город Л?

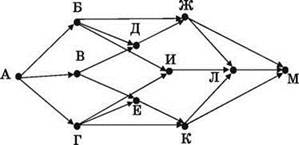
Решение

1) Возле города А записываем единицу. Это — некое “стартовое” значение, поскольку уж один-то путь из А в М есть всегда.

2) Смотрим город Б. В этот узел графа входит только одна стрелка, которая идёт от узла А со значением 1. Поэтому возле узла Б тоже записываем единицу.

3) То же с городами (узлами) В и Г — в них по единственной входящей стрелке “переносится” все та же единица из узла А.

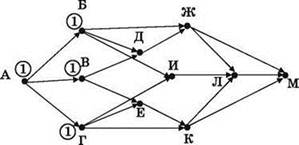
4) Смотрим город Д. В него входит две стрелки. Одна идёт из узла Б и “несёт с собой” оттуда единицу. Вторая же аналогичным способом переносит единицу по стрелке из узла В. Итого в узле Д в сумме получается значение 2 (1+1).

5) То же самое получается и для узла Е, куда по соответствующим двум стрелкам “приходят” единицы из узлов В и Г.

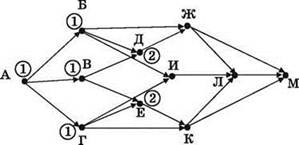
6) В узел Ж тоже входят две стрелки. Одна (из узла Б) “приносит” туда единицу. А вторая (из узла Д) “приносит” уже двойку. Итого в сумме получается 3 (1+2).

7) Для узла К история та же — рядом с ним тоже записываем 3 (1 по стрелке из узла Г плюс 2 по стрелке из узла Е).

8) Для узла же И две стрелки “принесут” с собой из узлов Б и Г по единице каждая, итого в сумме получаем 2.

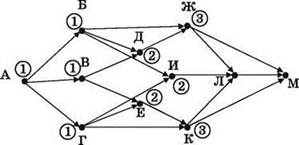
9) А теперь переходим к самому сложному узлу — Л. В него входит три стрелки. Первая, из узла Ж, “переносит” в Л тройку. Вторая, из узла К, “переносит” тоже тройку. И, наконец, третья, из узла И, “переносит” в Л двойку. В сумме же для Л получается значение 8 (3+2+3).

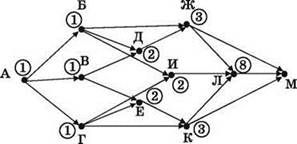
10) Остаётся узел М. В него приходит тоже три стрелки. Стрелка из узла Ж “приносит” в М тройку. Стрелка из узла К “приносит” в М тоже тройку. А стрелка из узла Л приносит в М восьмерку. В сумме для М получается 14 (3+3+8).

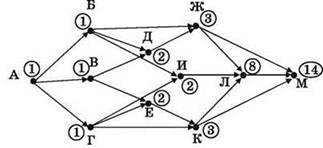
Ответ: 14.

Задача 5.

Схема дорог в некоторой области изображена в виде графа, а в таблице даны сведения о длинах этих дорог в километрах.

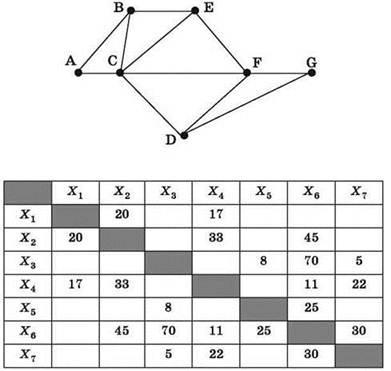
Эту таблицу и схему создавали разные люди независимо друг от друга, и обозначения посёлков в таблице никак не связаны с их обозначениями на графе.

Требуется определить длину дороги из пункта С в пункт D. Ответом является целое число — длина этой дороги.

Решение

1. Заметим, что С — это единственный пункт с 5-ю рёбрами. Ищем в таблице такой столбец (или строку), в котором содержится 5 значений. Тогда С — это Х₆.

2. Аналогично, F — это единственный пункт с 4-мя рёбрами. Тогда очевидно, что F — это Х₄.

3. С учётом этого получаем таблицу в следующем виде (ребро CF отмечаем закраской):

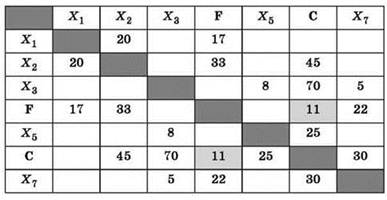
4. Пункт F, кроме пункта С, также связан с пунктами D, Е и G. При этом пункт G — единственный среди них, имеющий только 2 ребра. Просматриваем в таблице строку, соответствующую пункту F:

и ищем в столбцах, в которых в данной строке есть числовые значения (т.е. в графе есть рёбра между пунктом F и соответствующими другими пунктами), в каком столбце есть только два числа. Это — первый столбец. Значит, G — это Х₁:

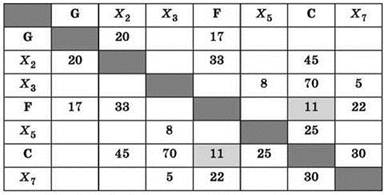
5. Пункт G связан с D и с F. Но столбец, соответствующий пункту F, мы уже определили. Тогда пункту D соответствует обозначение Х₂ (также отмечаем в таблице все уже найденные рёбра):

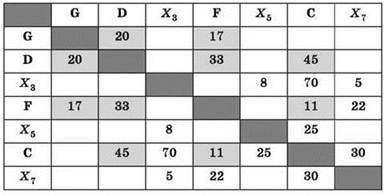
6. Тогда методом исключения получаем, что пункту Е соответствует обозначение Х₇:

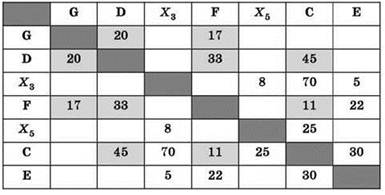
7. С пунктом С из числа ещё не рассмотренных связаны два пункта — В и А, причём пункт А — единственный с 2-мя рёбрами. Рассуждая аналогично предыдущему (см. п. 4), получаем, что А — это Х₅:

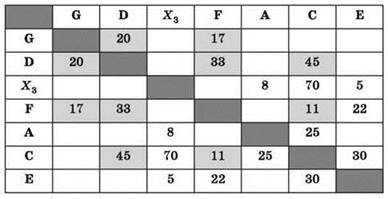
8. Очевидно, что оставшееся обозначение Х₃ соответствует пункту В:

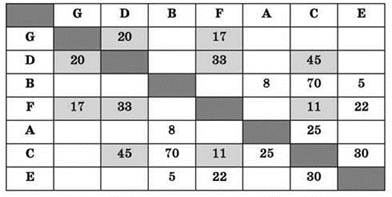
9. Итак, таблица полностью заполнена в соответствии с обозначениями пунктов на графе. Теперь по ней легко определить, что искомая длина пути (ребра) CD равна 45.

Ответ: 45.