Передача информации по коммуникационным каналам - Информация. Измерение информации. Кодирование информации

Конспект

Передача информации

Передача информации — это информационный процесс, при котором производится перемещение информации через пространство и/или через время от одного субъекта (источника информации) к другому субъекту (приемнику информации). При этом информация передается в форме документа (записи на некотором физическом носителе) либо в форме сообщения (последовательности сигналов по каналу связи).

В процессе передачи информации возможны помехи: случайные искажения физических характеристик канала связи, которые являются носителем информации, либо повреждения физического носителя. Наличие таких помех вынуждает применять различные способы борьбы с ними, в том числе многократное резервирование документов либо многократную пересылку сообщений, применение специальных методов контроля и коррекции ошибок (контрольная сумма, код Хемминга и пр.).

Измерение скорости передачи информации

Скорость передачи информации по каналу связи (обычно рассматривается только передача сообщений¹) вычисляется как количество информации, переданной за одну секунду. Базовой единицей при этом является “бит в секунду” (бит/с, bits per second, bps); может также использоваться размерность “байт в секунду” и производные от нее величины (кб/с, Мб/с и пр.).

Для измерения скорости передачи информации также применяется единица, называемая “бод” (baud). Однако в бодах измеряется не собственно скорость передачи информации, а скорость изменения информационного параметра, являющегося носителем передаваемой информации. В частном случае (при синхронной двоичной передаче) скорость в бодах может быть равна скорости в битах в секунду. Однако, например, в современных модемах при одном изменении уровня несущего сигнала может передаваться больше одного бита информации (например, 4 бита), тогда скорости 2400 бод соответствует скорость передачи информации 9600 бит/с.

Не следует путать эти две величины: бод и бит/с!

Диаграммы процессов (сетевые диаграммы, диаграммы Ганта)

В некоторых задачах, связанных с процессами передачи информации (особенно в случаях, когда один процесс начинается по истечении заданного времени после начала другого) можно существенно облегчить их решение благодаря его наглядному представлению с помощью диаграмм процессов. Такие диаграммы также называют диаграммами Ганта — по имени их изобретателя, американского инженера, механика и специалиста по менеджменту Генри Лоуренса Ганта.

Типичная диаграмма Ганта представляет собой отрезки или прямоугольные полоски, размещённые вдоль горизонтальной шкалы времени, где каждый отрезок соответствует отдельной задаче (подзадаче) или процессу. Начало, конец и длина каждого такого отрезка соответствуют началу, концу и длительности соответствующего процесса, а сами такие отрезки обычно располагаются друг за другом со сдвигом по вертикали.

В современных диаграммах Ганта, построенных при помощи специальных программ — систем управления проектами, кроме временных зависимостей, также отображаются зависимости (связи) между задачами. Например, самым распространённым типом такой зависимости является связь “Окончание — Начало”, когда очередная задача начинается после окончания предыдущей:

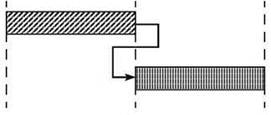
Для некоторых задач удобно рисовать подобную диаграмму, изображающую два процесса (или более) и размечая на ней временные отметки их начал и окончаний. Применение диаграммы Ганта для решения задач будет рассмотрено ниже.

Разбор типовых задач

Задача 1.

У Кати есть доступ в Интернет по высокоскоростному одностороннему радиоканалу, обеспечивающему скорость получения информации 2²⁰ бит в секунду. У Сергея нет скоростного доступа в Интернет, но есть возможность получать информацию от Кати по телефонному каналу со средней скоростью 2¹³ бит в секунду. Сергей договорился с Катей, что она скачает для него данные объёмом 9 Мбайт по высокоскоростному каналу и ретранслирует их Сергею по низкоскоростному каналу.

Компьютер Кати может начать ретрансляцию данных не раньше, чем им будут получены первые 1024 Кбайт этих данных. Каков минимально возможный промежуток времени (в секундах) с момента начала скачивания Катей данных до полного их получения Сергеем?

Решение

Создаётся набросок сетевой диаграммы, соответствующей условию задачи. Рассматриваются два процесса передачи, осуществляемые с разной скоростью, из которых один процесс начинается спустя заданное время после начала другого. Общий вид диаграммы имеет вид:

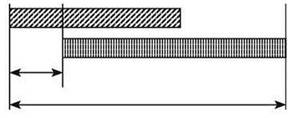
Процесс 1: компьютер Кати скачивает файл объёмом в 9 Мб (= 9 ∙ 2²⁰ байт = 9 ∙ 2²³ бит) со скоростью 2²⁰ бит/с.

Длительность процесса 1: 9 ∙ 2²³ / 2²⁰ = 9 ∙ 2³ с.

Процесс 2: компьютер Сергея скачивает файл объёмом в 9 Мб (= 9 ∙ 2²³ бит) со скоростью 2¹³ бит/с.

Длительность процесса 2: 9 ∙ 2²³ / 2¹³ = 9 ∙ 2¹⁰ с.

Начало процесса 2 — через время, равное времени скачивания со скоростью 2²⁰ бит/с информации объёмом 1024 кб (= 1024 ∙ 2¹⁰ байт = 2¹⁰ ∙ 2¹⁰ байт = 2²⁰ байт = 2²³ бит), т.е. через 2²³ / 2²⁰ = 2³ с.

Сетевая диаграмма с надписанными результатами расчётов:

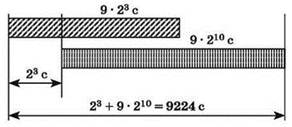
Благодаря сетевой диаграмме нетрудно определить, какие величины нужно суммировать для вычисления общей длительности процесса (т.е. времени, прошедшего с момента начала скачивания Катей данных до полного их получения Сергеем).

Ответ: 9224 с.

Следует не забывать приводить все величины, указанные в условии задачи, к одной размерности! Например, если скорость передачи информации задана в битах в секунду, то все значения объёмов информации нужно преобразовать в биты.

Задача 2.

Лена скачивает дистрибутив ОС Linux с зарубежного сайта-репозитория, пользуясь односторонним каналом цифровой передачи данных через телевизионное эфирное вещание, обеспечивающим приём информации со скоростью 4 Мбит/с. При этом информация передаётся фрагментами по 10 Мбайт. Для начала передачи каждого фрагмента компьютер Лены должен отправить на сервер сообщение-запрос объёмом 32 кбайт, а после получения фрагмента подтвердить его безошибочный приём отдельным сообщением объёмом 16 кбайт. Для отправки таких сообщений Лена пользуется радиомодемом GPRS, который обеспечивает скорость передачи информации 128 кбит/с. Определить минимально возможное время, за которое Лена сможет скачать файл дистрибутива объёмом 350 Мбайт.

Решение

Принцип решения данной задачи аналогичен предыдущей.

Общий вид сетевой диаграммы:

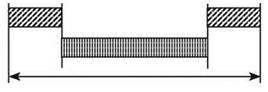
Процесс 1: передача сообщения-запроса объёмом 32 Кбайт (= 2⁵ ∙ 2¹⁰ байт = 2⁵ ∙ 2¹³ бит) через радиомодем GPRS со скоростью 128 Кбит/с (= 2⁷ ∙ 2¹⁰ бит/с).

Длительность процесса 1: 2⁵ ∙ 2¹³ / 2⁷ ∙ 2¹⁰ = 2¹⁸ / 2¹⁷ = 2 с.

Процесс 2: приём очередного фрагмента файла объёмом 10 Мбайт (= 10 ∙ 2²⁰ байт = 10 ∙ 2²³ бит) через телевизионное эфирное вещание со скоростью 4 Мбит/с (= 2² ∙ 2²⁰ бит/с).

Длительность процесса 2: 10 ∙ 2²³ / 2² ∙ 2²⁰ = 10 ∙ 2²³ / 2²² = 20 с.

Процесс 3: передача сообщения-подтверждения объёмом 16 Кбайт (= 2⁴ ∙ 2¹⁰ байт = 2⁴ ∙ 2¹³ бит) через радиомодем GPRS со скоростью 128 Кбит/с (= 2⁷ ∙ 2¹⁰ бит/с).

Длительность процесса 1: 2⁴ ∙ 2¹³ / 2⁷ ∙ 2¹⁰ = 2¹⁷ / 2¹⁷ = 1 с.

Файл объёмом 350 Мбайт принимается порциями по 10 Мбайт, следовательно, весь процесс приёма информации состоит из 35 элементарных процессов, рассмотренных выше (передача команд + приём очередного фрагмента).

Сетевая диаграмма с надписанными результатами расчётов:

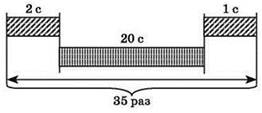
Итого для приёма всего файла потребуется 35 ∙ 23 = 805 с.

Ответ: 805 с.

Лучше разделить описываемый процесс передачи информации на отдельные повторяющиеся этапы, чтобы вначале определить длительность отдельного такого этапа, а затем вычислить общую длительность процесса.

Задача 3.

Данные объёмом 80 Мбайт передаются из пункта А в пункт Б по каналу связи, обеспечивающему скорость передачи данных 2²³ бит в секунду, а затем из пункта Б в пункт В по каналу связи, обеспечивающему скорость передачи данных 2²⁰ бит в секунду. От начала передачи данных из пункта А до их полного получения в пункте В прошло 13 минут.

Через какое время в секундах началась передача данных в пункте Б, т.е. каково время между началом передачи данных из пункта А и началом передачи данных в пункт В? В ответе укажите только число, слово “секунд” или букву “с” добавлять не нужно.

Решение

Если в предыдущих задачах нужно было искать общее время передачи данных из А в В, то теперь требуется составлять уравнение с одним неизвестным.

1) Построим диаграмму Ганта для этой задачи:

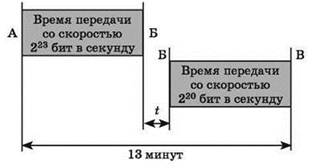
При этом следует учитывать, что процесс передачи данных из Б в В по условию задачи начинается уже после того, как завершится передача данных из А в Б.

2) Составляем по этой схеме уравнение (t — время задержки между окончанием приема данных из А и началом их передачи в В). Для этого вычисляем время передачи данных из А в Б и из Б в В:

• из А в Б: 80 (Мбайт) / 2²³ (бит в секунду) = 5 ∙ 2²⁷ (бит) / 2²³ (бит в секунду) = 5 ∙ 2⁴ = 80 (с);

• из Б в В: 80 (Мбайт) / 2²⁰ (бит в секунду) = 5 ∙ 2²⁷ (бит) / 2²⁰ (бит в секунду) = 5 ∙ 2⁷ = 640 (с).

Записываем уравнение:

80 + t + 640 = 13 (минут) = 13 ∙ 60 (с), т.е. 720 + t = 780, откуда t = 60.

3) Чтобы найти время от начала передачи данных из Л в Б до начала их передачи из Б в В, нужно к найденному значению t прибавить время передачи данных из А в Б:

80 + 60 = 140 (с).

Ответ: 140.

Задача 4.

Документ объёмом 8 Мбайт можно передать с одного компьютера на другой двумя способами:

А) сжать архиватором, передать архив по каналу связи, распаковать;

Б) передать по каналу связи без использования архиватора.

Какой способ быстрее и насколько, если:

• средняя скорость передачи данных по каналу связи составляет 2¹⁵ бит в секунду;

• объём сжатого архиватором документа равен 40% от исходного;

• время, требуемое на сжатие документа — 6 секунд, на распаковку — 3 секунды?

В ответе напишите букву А, если способ А быстрее, или Б, если быстрее способ Б. Сразу после буквы напишите, на сколько секунд один способ быстрее другого.

Например, если способ Б быстрее способа А на 23 секунды, в ответе нужно написать Б23.

Решение (вариант 1)

В данной задаче не требуется строить сетевую диаграмму, — только расчёты нужно выполнить дважды, для обоих предложенных вариантов (А и Б).

Вариант А:

Предполагается, что исходный массив информации сначала архивируется (6 секунд). Затем он в уже упакованном виде (40% от исходного объёма) передаётся по каналу связи с заданной средней скоростью, а после этого распаковывается (3 секунды).

Записывается соответствующая цепочка вычислений:

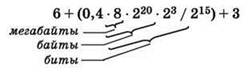
После некоторого количества арифметических операций вычисляется длительность всего процесса в секундах.

Вариант Б:

Аналогичным образом записываются вычисления времени передачи неупакованного массива информации по каналу связи:

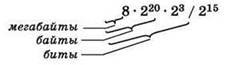
Выполнив вычисления и сравнив результат с полученным для варианта А, определяется ответ к задаче.

Решение (вариант 2)

Более экономичный способ решения задачи — вычисления выполняются только один раз.

Сравнивая предлагаемые варианты (А и Б) получается, что 40% от исходного объёма массива информации приходится передавать по каналу связи в обоих случаях. Различие же состоит в следующем.

В варианте А, кроме этих 40% объёма файла, по каналу связи больше ничего передавать не требуется, но зато имеются “накладные расходы” времени на упаковку/распаковку в количестве 6 + 3 = 9 секунд.

В варианте Б этих дополнительных расходов времени нет, но зато приходится передавать по каналу связи оставшиеся 60% объёма файла.

Получается, что для решения задачи достаточно сравнить между собой затраты времени именно на эти различающиеся в вариантах А и Б операции:

Другими словами, достаточно вычислить время передачи по каналу связи с заданной скоростью 60% исходного объёма информации и вычесть из этого времени 9 секунд:

• если результат отрицателен, то быстрее способ Б;

• если результат положителен, то быстрее способ А;

• если результат равен нулю, то оба способа равнозначны по скорости;

• абсолютное значение (модуль) разности — это и есть искомое время, на которое один способ быстрее другого.

В данном случае:

Ответ: А1219,8 (способ А быстрее способа Б на 1219,8 секунды).

Рекомендуется большие числа преобразовывать в произведения некоторой константы (не кратной 2) на соответствующую степень двойки. Это облегчает выполнение операций умножения и деления (благодаря возможности сокращения двоек) и уменьшает вероятность ошибок в вычислениях.

Задача 5.

Документ объёмом 50 Мб можно передать с одного компьютера на другой двумя способами:

А) сжать архиватором, передать по каналу связи архив, распаковать его;

Б) сжать суперархиватором, передать суперархив по каналу связи, распаковать его.

При этом:

• скорость передачи данных по каналу связи составляет 2²² бит/с;

• объем архива составляет 75% от исходного файла;

• объём суперархива составляет 50% от исходного файла;

• сжатие документа архиватором занимает 15 с, а распаковка — 10 с;

• сжатие документа суперархиватором занимает 30 с, а распаковка — 15 с.

Какой способ быстрее и насколько?

В ответе надо записать сначала букву, обозначающую соответствующий способ, а затем сразу после нее записать количество секунд, на сколько этот способ быстрее другого. Например, если способ А быстрее способа Б на 30 секунд, то надо записать ответ в виде А30.

Решение

Задача решается аналогично предыдущей, только здесь лучше честно вычислить время, затрачиваемое на сжатие, передачу и распаковку информации в каждом из двух способов, а потом сравнить результаты.

А) Тратим 25 секунд на сжатие/распаковку, а затем передаем 75% от 50 Мб со скоростью 2²² бит/с:

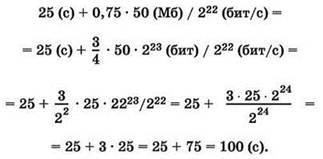
Б) Тратим 45 секунд на сжатие/распаковку, а затем передаем 50% от 50 Мб со скоростью 2²² бит/с:

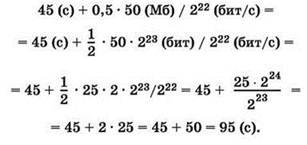
Сравнивая способы А и Б, получаем, что быстрее способ Б на 5 секунд.

Ответ: Б5.

---

¹ В случае с записью документов на физическом носителе, в принципе, тоже можно вычислить скорость “передачи информации” исходя из скорости перемещения носителя и его объёма, однако обычно такие расчёты выполняются и приводятся только как курьёз.