Деление и дроби - Урок 2 - ОБЫКНОВЕННЫЕ ДРОБИ - ДРОБНЫЕ ЧИСЛА

Основная дидактическая цель урока: учить заменять частное дробью и дробь — частным, использовать дробную черту в записи уравнений.

Ход урока

I. Организационный момент. Определение темы урока

На доске (слайде):

— Рассмотрите записи.

— Какая между ними связь?

— Какой знак можно поставить между ними?

— Кто догадался, какой будет тема нашего сегодняшнего урока?

II. Устный счет

1. Найдите значения выражений удобным способом.

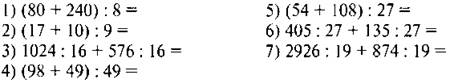
2. Кусок провода длиной 3 м разрезали на 5 равных частей. Чему равна длина каждой части? (3/5 м.)

3. Ученики решили отремонтировать 36 парт. За неделю они отремонтировали 1/4 всего количества. Сколько парт им осталось отремонтировать? (27.)

4. Бригада рабочих проложила 200 м дороги. Оказалось, что это 5/7 всего участка дороги. Найдите протяженность всего участка. (280 м.)

5. В поселке построили 27 домов, 3 из них многоэтажные. Какую часть составляют многоэтажные дома? (3/27.)

III. Работа по теме урока

(Фронтальная работа.)

— Запишите частные в виде дроби.

1 : 6 =

2 : 3 =

5 : 10 =

5 : 6 =

— Какая из дробей обозначает половину целого?

— Придумайте и запишите 5 дробей, которые обозначают половину целого, и замените их частным.

(Проверка выполнения задания.)

— Рассмотрите частные.

28 : 7; 1 : 2; 2 : 1; 1 : 6; 6 : 4; 12 : 12; 100 : 8.

— Выпишите в столбик только те частные, которые обозначают дробные числа.

— Объясните свой выбор.

1 : 2     1 : 6     6 : 4     100 : 8

— Замените эти частные дробью.

— Что заметили? (Получились правильные и неправильные дроби.)

(На доске записаны уравнения в два столбика.)

— Рассмотрите уравнения правого и левого столбика. Что вы заметили? (В правом и левом столбике записаны одни и те же уравнения.)

— Соедините их попарно.

— Решите уравнения из правого столбика.

IV. Работа над задачами

1. С. 165, № 1070 (устно).

— Сколько частей из 10 пошло на брюки?

— Какая это часть целого?

— Сколько частей из 10 пошло на куртки?

— Какая это часть целого?

2. С. 166, № 1073 (работа в паре).

Проверка

Пусть время движения на поверхности будет х.

Тогда время движения под водой будет 20х.

Разница во времени равна 20х — х.

А по условию она составляет 57 ч.

Значит, можем составить уравнение:

20х - х = 57

19х = 57

х = 57 : 19

х = 3 (ч) — время движения на поверхности.

20 ∙ 3 = 60 (ч) — время движения под водой.

— Как иначе можно найти время движения под водой? (3 + 57 = 60.)

(Вторую задачу учащиеся решают самостоятельно.)

Проверка

Пусть путь по поверхности составляет х км.

Тогда путь под водой будет 17х км.

Разница расстояний составляет (17х — х) км.

А по условию задачи она равна 320 км.

Значит, можем составить уравнение:

17х — х = 320

16х = 320

х = 320 : 16

х = 20 (км) — путь по поверхности.

20 ∙ 17 = 340 (км) — путь под водой.

3. С. 166, № 1071.

— Сколько разных вариантов выбора имеет первый ребенок? (4.)

— Сколько возможных вариантов выбора останется второму ребенку? (3.)

— Сколько существует разных вариантов выбора для первого и второго ребенка? (4 ∙ 3 = 12.)

— Сколько вариантов осталось для третьего и четвертого? (2 и 1.)

— Как записать решение этой задачи? (4 ∙ 3 ∙ 2 ∙ 1 = 4! = 24 варианта.)

V. Повторение изученного материала

С. 164, № 1058 (работа в паре).

Проверка

VI. Рефлексия

— Оцените свою работу на уроке.

Домашнее задание

С. 167, № 1079, 1080.