Поурочные разработки по алгебре 7 класс - к учебнику Ю.Н. Макарычева - 2014 год
Тождества - ПРЕОБРАЗОВАНИЕ ВЫРАЖЕНИЙ - ВЫРАЖЕНИЯ, ТОЖДЕСТВА, УРАВНЕНИЯ
Цель: сформировать представление о тождественно равных выражениях и тождестве.
Планируемые результаты: иметь представление о тождестве.
Тип урока: урок-исследование.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (письменный опрос).
Вариант 1
1. Дайте формулировку (алгебраическую и словесную) переместительного свойства для сложения и умножения.
2. Вычислите наиболее рациональным способом:
![]()
3. Вычислите значение выражения (3 - а) + (а - 2) + (4 - а) + (а - 1).
Вариант 2
1. Дайте формулировку (алгебраическую и словесную) сочетательного свойства для сложения и умножения.
2. Вычислите наиболее рациональным способом:
![]()
3. Вычислите значение выражения (2 - b) + (b + 5) + (4 - b) + (b - 3).
III. Работа по теме урока
Пример 1
Найдем значения двух алгебраических выражений х2 и 5 ∙ x - 6 при одном и том же значении переменной, например х = 1. Получаем значения этих выражений: (1)2 = 1 и 5 ∙ 1 - 6 = -1. Видно, что соответственные значения выражений не равны. Теперь найдем соответственные значения этих выражений при х = 2. Получаем значения: (2)2 = 4 и 5 ∙ 2 - 6 = 4. В этом случае значения выражений равны.
Существуют и такие выражения, соответственные значения которых равны при любых допустимых значениях переменных. Такие выражения называются тождественно равными.
Пример 2
а) В соответствии с переместительным и сочетательным свойствами сложения выражения а + b + с; b + а + с; (а + b) + с; а + (b + с); (а + с) + b и т. д. являются тождественно равными при всех значениях а, b и с.
б) В соответствии с основным свойством дроби выражения ![]() являются тождественно равными при всех допустимых значениях переменных а, b и с, т. е. при любых значениях а, b (кроме b= 0) и с (кроме с = 0), или при b ≠ 0 и с ≠ 0.
являются тождественно равными при всех допустимых значениях переменных а, b и с, т. е. при любых значениях а, b (кроме b= 0) и с (кроме с = 0), или при b ≠ 0 и с ≠ 0.
в) В соответствии с основным свойством дроби выражения ![]() являются тождественно равными при а ≠ 1 и b ≠ 2.
являются тождественно равными при а ≠ 1 и b ≠ 2.
Равенство, связывающее два тождественно равных выражения, называется тождеством.
Пример 3
Являются тождествами при всех допустимых значениях переменных равенства:
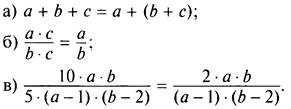
Верные числовые равенства также считаются тождествами.
Пример 4
Являются тождествами равенства:
![]()
IV. Задания на уроке
№ 85 (а, б), 86 (а, в), 87 (а, в), 88 (а, б), 90 (а, в), 91 (а), 92 (а), 93 (а, б).
V. Контрольные вопросы
— Какие значения алгебраических выражений являются соответственными?
— Могут ли соответственные значения выражений быть а) равными; б) неравными?
— Какие выражения называются тождественно равными? Приведите примеры.
— Какое равенство называется тождеством? Приведите примеры.
— В каком случае числовое равенство будет тождеством? Приведите примеры.
VI. Творческие задания
1. Проверьте, являются ли тождественно равными выражения:
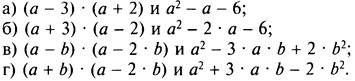
2. При каких допустимых значениях переменных равенства являются тождествами?
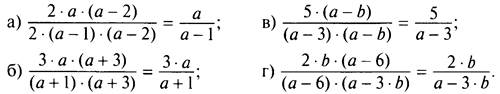
3. Укажите значения переменных, при которых равны соответственные значения выражений:
![]()
VII. Подведение итогов урока
Домашнее задание
№ 85 (в, г), 86 (б, г), 87 (б, г), 88 (в, г), 90 (б, г), 91 (б), 92 (б), 93 (в, г).