Поурочные разработки по алгебре 7 класс - к учебнику Ю.Н. Макарычева - 2014 год
Линейное уравнение с одной переменной - УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ - ВЫРАЖЕНИЯ, ТОЖДЕСТВА, УРАВНЕНИЯ
Цель: сформировать представление о линейном уравнении и его решении.
Планируемые результаты: освоить навыки решения линейных уравнений.
Тип урока: урок общеметодологической направленности.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (письменный опрос).
Вариант 1
1. Что называется уравнением с одним неизвестным?
2. Составьте уравнение, которое имеет корни -2 и 5.
3. Проверьте, являются ли уравнения равносильными:
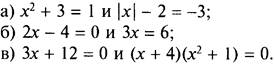
Объясните почему.
Вариант 2
1. Что называется корнем уравнения с одним неизвестным?
2. Составьте уравнение, которое имеет корни - 3 и 6.
3. Проверьте, являются ли уравнения равносильными. Объясните почему.
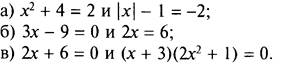
III. Работа по теме урока
План урока
1. Линейное уравнение.
2. Решение линейных уравнений.
1. Линейное уравнение
Уравнение вида а ∙ х = b (где х — переменная, а и b — некоторые числа) называется линейным уравнением с одной переменной. Отличительная особенность такого уравнения — переменная х входит в уравнение обязательно в первой степени.
Пример 1
Перечисленные уравнения являются линейными, так как имеют вид а ∙ х = b;
а) 3 ∙ х = 7 (где а = 3, b = 7);
б) -2 ∙ х = 5 (где а = -2, b = 5);
в) 0 ∙ х = -5 (где а = 0, b = -5);
г) 0 ∙ х = 0 (где а = 0, b = 0).
Все линейные уравнения приводятся к стандартному виду а ∙ х = b при помощи тождественных преобразований.
Пример 2
В уравнение 2(3х - 5) = х - 3 переменная х входит в первой степени, поэтому оно является линейным. Приведем это уравнение к стандартному виду. В левой части раскроем скобки: 2 ∙ 3х - 2 ∙ 5 = х - 3 или 6х - 10 = х - 3.
Перенесем слагаемые, содержащие переменную х, в левую часть уравнения, числа — в правую. Приведем подобные члены. Получаем 6х - х = 10 - 3 или 5х = 7.
Линейное уравнение имеет стандартный вид а ∙ х = b (где а = 5, b = 7).
Пример 3
Не является линейным уравнение:
а) 3х2 + 6х + 7 = 0, так как содержит переменную х во второй степени (слагаемое 3 ∙ х2);
б) 6х + 2|х| = 3, так как содержит величину |х|;
в) 2х3 + 5х = 4, так как содержит переменную х в третьей степени.
2. Решение линейных уравнений
При решении линейного уравнения а ∙ х = b возможны три случая:
1. Если число а ≠ 0, то уравнение имеет один корень х = b/a.
2. Если числа а = 0 и b = 0, то уравнение имеет бесконечно много корней (любое число является его корнем).
3. Если числа а = 0 и b ≠ 0, то уравнение корней не имеет.
Пример 4
Решим уравнение 2(3х - 1) = 4(х + 3).
Приведем его к стандартному виду. Раскроем скобки в обеих частях уравнения: 2 ∙ 3х - 2 ∙ 1 = 4х + 4 ∙ 3 или 6х - 2 = 4х + 12. Слагаемые, зависящие от переменной х, перенесем в левую часть уравнения, числа — в правую, изменив их знаки на противоположные: 6х - 4х = 2 + 12. Приведем подобные слагаемые: 2х = 14. В этом уравнении а = 2 (очевидно, а ≠ 0) и b = 14. Уравнение имеет один корень ![]()
Пример 5
Решим уравнение 2(3х - 1) = 4(х + 3) - 14 + 2х.
Приведем его к стандартному виду: 6х - 2 = 4х + 12 - 14 + 2x или 6х - 4х - 2х = 2 + 12 - 14, или 0 ∙ х = 0 (где а = 0, b = 0). Очевидно, что при подстановке любого значения х получаем верное числовое равенство 0 = 0. Поэтому любое число является корнем этого уравнения (уравнение имеет бесконечно много корней).
Пример 6
Решим уравнение 2(3х - 1) = 4(х + 3) + 2х.
Приведем это уравнение к стандартному виду: 6х - 2 = 4х + 12 + 2х, или 6х - 4х - 2х = 12 + 2, или 0 ∙ х = 14 (где а = 0, b = 14). Очевидно, что при подстановке любого значения х получаем неверное числовое равенство 0 = 14. Поэтому уравнение корней не имеет.
IV. Задания на уроке
№ 126 (а, в, е, з), 127 (б, в, д), 128 (е, з), 129 (а, в, д, к).
V. Контрольные вопросы
— Напишите стандартный вид линейного уравнения.
— Какое уравнение является линейным?
— Перечислите возможные случаи решения линейных уравнений.
VI. Подведение итогов урока
Домашнее задание
№ 126 (б, д, ж, и), 127 (а, г, е), 128 (ж, и), 129 (б, е, з, и).