Числовые (арифметические) выражения - ВЫРАЖЕНИЯ - ВЫРАЖЕНИЯ, ТОЖДЕСТВА, УРАВНЕНИЯ

Цели: ознакомить с числовыми выражениями и основными понятиями; напомнить, как выполнять действия над обыкновенными дробями.

Планируемые результаты: усвоить понятия числового выражения и его значения, выражения, не имеющего смысла; вспомнить действия над обыкновенными дробями.

Тип урока: урок повторения изученного материала.

Ход урока

I. Сообщение темы и целей урока

II. Работа по теме урока

План урока

1. Числовое выражение.

2. Значение числового выражения.

3. Обыкновенные дроби и действия над ними.

1. Числовое выражение

Запись, составленная из чисел с помощью арифметических действий (сложение, вычитание, умножение, деление, возведение в степень) и скобок, называется числовым (арифметическим) выражением. В частности, сами числа также можно рассматривать как числовые выражения.

Пример 1

Числовые выражения:

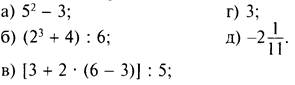
(Учитель просит учащихся привести свои примеры числовых выражений.)

Очень часто числовые выражения возникают при решении задач с текстовым содержанием.

Пример 2

В саду на даче растут 5 яблонь, 4 вишни и 3 сливы. Было собрано по 30 кг плодов с яблони, 10 кг — с вишни и 15 кг — со сливы. Какой урожай фруктов и ягод собрали в саду?

Решение

Так как с каждой яблони было собрано 30 кг плодов, то с 5 яблонь собрали 30 ∙ 5 кг. Так как с каждой вишни было собрано 10 кг плодов, то с 4 вишен собрали 10 ∙ 4 кг. Так как с каждой сливы было собрано 15 кг, то с 3 слив собрали 15 ∙ 3 кг. Общий урожай фруктов и ягод равен сумме собранных плодов с яблонь, вишен и слив, т. е. 30 ∙ 5 + 10 ∙ 4 + 15 ∙ 3.

Решая задачу, получили числовое выражение

30 ∙ 5 + 10 ∙ 4 + 15 ∙ 3.

Забегая вперед, вычислим значение этого выражения:

30 ∙ 5 + 10 ∙ 4 + 15 ∙ 3 = 150 + 40 + 45 = 235 (кг).

Пример 3

Найдите периметр (сумму длин всех сторон) прямоугольника со сторонами 4 см и 6 см.

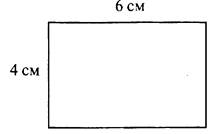
Решение

1-й способ

Можно посчитать непосредственно сумму длин сторон прямоугольника. Тогда получаем числовое выражение 4 + 6 + 4 + 6 или 6 + 4 + 6 + 4 (в зависимости от того, с какой стороны считаем сумму длин сторон).

2-й способ

Найдем сумму длин меньших сторон (4 ∙ 2 см) и сумму длин больших сторон (6 ∙ 2 см). Тогда сумма длин всех сторон (периметр прямоугольника) описывается числовым выражением 4 ∙ 2 + 6 ∙ 2.

3-й способ

Найдем полупериметр прямоугольника — сумму длин меньшей и большей сторон: 4 + 6. Учтем, что прямоугольник имеет две меньшие и две большие стороны. Тогда периметр описывается числовым выражением 2 ∙ (4 + 6).

Периметр прямоугольника равен 20 см.

Таким образом: а) по условию задачи можно составить разные числовые выражения; б) независимо от формы записи числового выражения результат его вычисления будет один и тот же (учитывая свойства арифметических действий).

Пример 4

Поезд ехал сначала 50 мин со скоростью 60 км/ч, затем остановился на станции на 10 мин, после чего двигался еще 1 ч со скоростью 40 км/ч. Найдите среднюю скорость движения поезда.

Решение

В соответствии с определением средняя скорость движения равна отношению пройденного пути к затраченному на этот путь времени.

Вычислим путь и время движения. Прежде всего, учтем, что (приведение к одинаковым единицам измерения времени). В начале движения был пройден путь в конце движения — путь 40 ∙ 1 (км).

Общий пройденный путь описывается числовым выражением

Время, затраченное на этот путь (включая время на остановку), описывается числовым выражением

Тогда средняя скорость движения описывается числовым выражением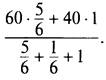

Вычислим значение этого выражения:

2. Значение числового выражения

Число, которое получается в результате выполнения арифметических действий в числовом выражении, называется значением числового выражения.

Может оказаться, что в числовом выражении какое-то действие невыполнимо, тогда выражение не имеет смысла. Пока вам известно только одно невыполнимое действие — деление на нуль (в дальнейшем вы узнаете и другие такие действия: извлечение корня четной степени из отрицательных чисел, нахождение логарифма неположительных чисел и т. д.).

Пример 5

Найдите значение числового выражения

Решение

Выполним действия в данном выражении:

Итак, значение числового выражения равно 1.

Пример 6

Найдите значение числового выражения:

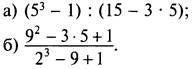
Решение

Данные числовые выражения не имеют смысла, так как делить на нуль нельзя.

3. Обыкновенные дроби и действия над ними

(Необходимо вкратце напомнить учащимся о том, как выполнять действия над дробями.)

Обыкновенной дробью называется число вида m/n, где m и n — натуральные числа. Например:

Число m называют числителем, число n — знаменателем дроби. Всякое целое число можно рассматривать как обыкновенную дробь со знаменателем 1. Например:

При действиях над дробями используется основное свойство дроби: если числитель и знаменатель данной дроби умножить или разделить на одно и то же (не равное нулю) число, то получится дробь, равная данной дроби. Например:

Сокращение дроби: нужно числитель и знаменатель разложить на простые множители, найти их наибольший общий делитель (НОД) и поделить числитель и знаменатель на НОД.

Пример 7

Сократите дробь 105/147.

Решение

Раскладываем числитель и знаменатель на простые множители: 105 = 3 ∙ 5 ∙ 7 и 147 = 3 ∙ 7 ∙ 7. Находим НОД чисел 105 и 147: НОД (105, 147) = 3 ∙ 7 = 21. Используя основное свойство дроби, делим ее числитель и знаменатель на НОД. Получаем

Приведение дроби к другому знаменателю: нужно числитель и знаменатель умножить на дополнительный множитель.

Пример 8

Приведите дробь 5/7 к знаменателю 42.

Решение

Старый (7) и новый (42) знаменатели различаются в 6 раз. Поэтому в соответствии с основным свойством дроби числитель и знаменатель данной дроби умножим на дополнительный множитель 6. Получаем

Приведение нескольких дробей к общему знаменателю: нужно найти общий знаменатель дробей (он равен наименьшему общему кратному (НОК) знаменателей всех дробей) и привести каждую дробь к этому знаменателю (аналогично примеру 8).

Пример 9

Приведите дроби к общему знаменателю.

Решение

Раскладываем знаменатели дробей на простые множители: 105 = 3 ∙ 5 ∙ 7 и 147 = 3 ∙ 7². Находим НОК чисел 105 и 147: НОК (105, 147) = 3 ∙ 5 ∙ 7² = 735. Число 735 будет общим знаменателем данных дробей. Находим дополнительный множитель для каждой дроби. Для этого поочередно делим общий знаменатель на знаменатель каждой дроби.

Получаем дополнительный множитель к первой дроби: — и ко второй дроби: Умножим числитель и знаменатель каждой дроби на найденный дополнительный множитель. Получаем

Сложение (вычитание) дробей: нужно сложить (вычесть) дроби с одинаковыми знаменателями. При этом знаменатель суммы (разности) остается прежним, а числители складываются (вычитаются). Если дроби имеют разные знаменатели, их предварительно приводят к общему знаменателю.

Пример 10

Выполните действия:

Решение

а) В предыдущем примере эти дроби уже были приведены к общему знаменателю. Поэтому получаем

Полученную дробь можно сократить:

б) Разность данных дробей:

Вспомним еще некоторые понятия.

Дробь, у которой числитель меньше знаменателя, называется правильной. Например:

Дробь, у которой числитель больше знаменателя либо равен ему, называется неправильной. Например:

Из неправильной дроби можно выделить целую часть. Например:

Число, состоящее из целой и дробной части, называется смешанным.

В ряде случаев сложение и вычитание смешанных чисел удобно выполнять отдельно с целыми и дробными частями.

Пример 11

Сложите числа

Решение

Получаем

При умножении дробей получается дробь, числитель которой равен произведению числителей данных дробей, а знаменатель — произведению знаменателей дробей. Если возможно, то полученную дробь надо сократить. При умножении смешанные числа обращают в неправильные дроби.

Пример 12

Перемножьте числа

Решение

Прежде всего, смешанное число обратим в неправильную дробь: 5 58

Умножим дроби получим

Два числа называются взаимно обратными, если их произведение равно единице. Например:

При делении дробей надо делимое умножить на число, обратное делителю.

Пример 13

Разделите дробь на число

Решение

Обратим смешанное число в неправильную дробь:

Разделим дробь на дробь получим

III. Задания на уроке

1. Составьте числовые выражения, которые:

а) имеют смысл;

б) не имеют смысла.

Если выражение имеет смысл, то найдите его значение.

(Можно рекомендовать парную работу (например, соседи по парте): каждый учащийся определяет, имеет ли смысл выражение, записанное соседом, и объясняет почему. Если выражение имеет смысл, то находит его значение.)

Обратите внимание на то, что количество открывающихся и закрывающихся скобок, используемых в выражении, должно быть одинаковым.

2. По текстовой задаче составьте числовое выражение (по аналогии с примерами 4—6) и вычислите его значение.

(Учитель предлагает текстовую задачу.)

3. Обратная задача: по написанному простому числовому выражению составьте текстовую задачу.

(Учитель предлагает числовое выражение. Можно рекомендовать парную работу: соседи пишут выражения и обмениваются тетрадями, после этого составляют задачу по чужому выражению.)

4. Выполните действия (сложение и вычитание):

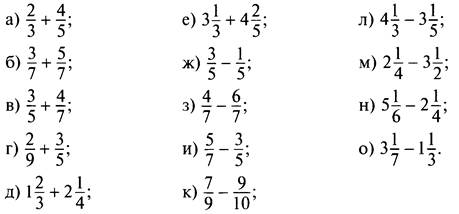
5. Выполните действия (умножение, деление, возведение в степень):

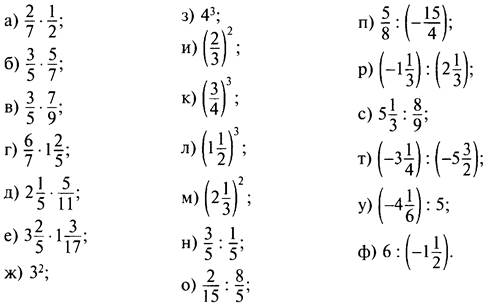
IV. Контрольные вопросы

(Опрос учащихся.)

— Что называется числовым выражением?

— В каком случае числовое выражение не имеет смысла?

— Что называется значением числового выражения?

— Какое число называется обыкновенной дробью?

— Назовите основное свойство дроби.

— Как сократить дробь?

— Как привести дроби к общему знаменателю?

— Как складываются (вычитаются) дроби?

— Какая дробь называется правильной? неправильной?

— Какое число называется смешанным?

— Как умножаются дроби? смешанные числа?

— Какие числа являются взаимно обратными?

— Как делятся дроби? смешанные числа?

V. Творческие задания

(Творческие задания можно использовать на уроке или дома.)

1. Используя четыре раза цифру 2, составьте выражение, значение которого равно 1, 2, 3, ..., 9 (если это возможно).

Например:

2. Установите закономерность и напишите три следующих числа в последовательности:

а) 3, 5, 7, 9, ... (арифметическая прогрессия, каждый член на два больше предыдущего);

б) 2, 5, 8, 11, ... (арифметическая прогрессия, каждый член на три больше предыдущего);

в) 3, 6, 12, 24, ... (геометрическая прогрессия, каждый член в два раза больше предыдущего);

г) 2, 6, 18, 54, ... (геометрическая прогрессия, каждый член в три раза больше предыдущего);

д) 1, 4, 9, 16, ... (квадраты натуральных чисел);

е) 1, 8, 27, 64, ... (кубы натуральных чисел);

ж) 1, 2, 3, 5, 8, ... (каждый член равен сумме двух предыдущих);

з) 1, 3, 4, 7, 11, ... (каждый член равен сумме двух предыдущих).

3. Найдите сумму дробей:

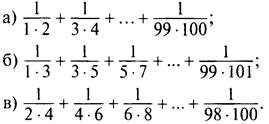
Решение

а) Надо учесть, что

Тогда данная сумма

(в сумме сокращаются все дроби, кроме первой и последней).

(Ответ: 99/100.)

б) Надо учесть, что

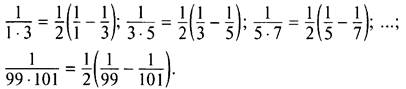
Тогда данная сумма

(Ответ: 50/101.)

в) Надо учесть, что

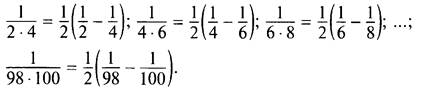
Тогда данная сумма

(Ответ: 49/200.)

4. Может ли дробь, в которой числитель меньше знаменателя, быть равной дроби, в которой числитель больше знаменателя? Если да, приведите пример.

(Ответ. Может. Например: )

5. Найдите наименьшее число, которое при делении на 2 дает остаток 1, при делении на 3 — остаток 2, при делении на 5 — остаток 4, при делении на 7 — остаток 6.

Решение

Рассмотрим число, которое на единицу больше данного. Тогда это число будет без остатка делиться на указанные числа: 2, 3, 5, 7. Эти числа простые. Поэтому наименьшее число, которое делится на 2, 3, 5, 7, — произведение этих чисел 2 ∙ 3 ∙ 5 ∙ 7 = 210. Искомое число на единицу меньше, т. е. 210 - 1 = 209.

6. Найдите наименьшее число, которое при делении на 2 дает остаток 1, при делении на 3 — остаток 2, при делении на 4 — остаток 3, при делении на 8 — остаток 7.

Решение

Рассмотрим число, которое на единицу больше данного. Тогда это число будет без остатка делиться на указанные числа: 2, 3, 4, 8. Однако эти числа не взаимно простые. Поэтому наименьшее число, которое делится на 2, 3, 4, 8, равно НОК этих чисел. НОК (2, 3, 4, 8) = 3 ∙ 8 = 24. Искомое число на единицу меньше, т. е. 24 - 1 = 23.

7. Найдите сумму чисел:

а) 1 + 2 + 3 + ... + 99 + 100.

(Ответ: 5050.)

Решение

Слагаемые являются членами арифметической прогрессии. Поэтому удобно сгруппировать первое слагаемое с последним, второе — с предпоследним и т. д. Получаем S = (1 + 100) + (2 + 99) + (3 + 98) + ... = 101 + 101 + ... + 101 = 101 ∙ 50 = 5050.

б) 1 + 3 + 5 + ... + 97 + 99.

(Ответ: 2500.)

в) 2 + 4 + 6 + ... + 98 + 100.

(Ответ: 2550.)

8. Один рыбак поймал 3 рыбины, второй — 5 рыбин. Из этих рыбин сварили уху. Мимо рыбаков шел прохожий, и рыбаки пригласили его пообедать. После того как уха была съедена рыбаками и прохожим, прохожий дал рыбакам 80 руб. за уху. Как по справедливости рыбаки должны поделить эти деньги?

Решение

Очевидно, что поровну (по 40 руб.) делить деньги нельзя, так как рыбаки для ухи дали разное количество рыбы. Но нельзя также первому рыбаку дать 30 руб., а второму — 50 руб., так как рыбаки и сами ели уху (такой дележ был бы справедливым, если бы рыбаки просто продали прохожему свою рыбу). На уху пошло 8 рыбин. Прохожий заплатил за то, что съел сам, т. е. за третью часть от 8 рыбин. Тогда все 8 рыбин стоят в три раза дороже, т. е. 80 ∙ 3 = 240 (руб.). Значит, одна рыбина стоит 30 руб. Поэтому 3 рыбины первого рыбака стоят 30 ∙ 3 = 90 (руб.). Но сам рыбак съел ухи на 80 руб., и ему причитается 90 - 80 = 10 (руб.). У второго рыбака 5 рыбин стоят 30 ∙ 5 = 150 (руб.). Но и этот рыбак съел ухи на 80 руб., и ему причитается 150 - 80 = 70 (руб.). Следовательно, справедливый дележ таков: первому рыбаку — 10 руб., второму — 70 руб.

VI. Подведение итогов урока

Домашнее задание

№ 4 (а, в, д, ж), 6 (а, б, г, и), 11, 13, 15.