Вычисление числовых выражений (десятичные дроби) - ВЫРАЖЕНИЯ - ВЫРАЖЕНИЯ, ТОЖДЕСТВА, УРАВНЕНИЯ

Цель: напомнить, как выполнять действия над десятичными дробями, порядок действий при вычислении выражений.

Планируемые результаты: отработать действия над десятичными дробями; вспомнить порядок действий при вычислении значений числовых выражений; рассмотреть основные задачи на проценты.

Тип урока: урок-практикум.

Ход урока

I. Сообщение темы и цели урока

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (письменный опрос).

Вариант 1

1. Что называется числовым выражением?

2. Выполните действия:

3. В школьном саду с 5 яблонь было собрано по 25 кг плодов, с 6 слив — по 15 кг и с 8 вишен — по 6 кг. Составьте числовое выражение для нахождения массы собранного урожая и вычислите его значение.

Вариант 2

1. Что называется значением числового выражения?

2. Выполните действия:

3. В школьном саду с 7 яблонь было собрано по 30 кг плодов, с 5 слив — по 12 кг и с 6 вишен — по 7 кг. Составьте числовое выражение для нахождения массы собранного урожая и вычислите его значение.

III. Работа по теме урока

План урока

1. Обыкновенные и десятичные дроби.

2. Действия над десятичными дробями.

3. Порядок действий при вычислении значений выражений.

4. Процент. Основные задачи на проценты.

1. Обыкновенные и десятичные дроби

Правильную дробь, знаменатель которой равен 10, 100, 1000 и т. д., можно записать в виде конечной десятичной дроби. Например: Таким же образом можно записать смешанное число или неправильную дробь с указанным знаменателем. Например: Если знаменатель дроби при разложении на простые множители содержит только числа 2 и 5 в различных степенях, то такую дробь также можно представить в виде конечной десятичной дроби, выполнив деление “уголком”.

Пример 1

Представьте обыкновенную дробь 11/40 в виде десятичной.

Решение

Разложим знаменатель дроби 11/40 на простые множители: 40 = 2³ ∙ 5. Такое разложение содержит только множители 2 и 5. Разделив “уголком” числитель на знаменатель, получим

В результате обыкновенная дробь представлена в виде конечной десятичной:

Если знаменатель дроби при разложении на простые множители содержит, кроме чисел 2 и 5, и другие числа, то такую дробь можно представить в виде бесконечной десятичной периодической дроби.

Пример 2

Представьте обыкновенную дробь 40/11 в виде десятичной.

Решение

Разделив “уголком” числитель на знаменатель, получим

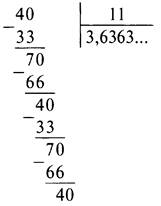
В результате обыкновенная дробь представлена в виде бесконечной десятичной периодической: Период десятичных дробей принято указывать в скобках.

Таким образом, любую обыкновенную дробь можно представить в виде десятичной (конечной или бесконечной периодической). Справедливо также обратное утверждение: любую конечную или бесконечную периодическую десятичную дробь можно представить в виде обыкновенной.

Конечную десятичную дробь сразу можно записать в виде дроби со знаменателем 10, 100 и т. д. (и выполнить, если необходимо, сокращение дроби).

Пример 3

Представьте дробь 0,128 в виде обыкновенной.

Решение

Получаем

Бесконечную десятичную периодическую дробь можно записать в виде обыкновенной, пользуясь следующим правилом:

1. Чтобы получить числитель дроби, нужно из числа, образованного цифрами, стоящими до второго периода, вычесть число, образованное цифрами, стоящими до первого периода.

2. Знаменатель дроби состоит из цифр 9 и 0. Цифра 9 повторяется столько раз, сколько было цифр в периоде, а цифра 0 — столько раз, сколько цифр содержится между запятой и первым периодом.

Пример 4

Представьте дробь 0,5(12) в виде обыкновенной.

Решение

До второго периода стоит число 512, до первого периода — число 5. Поэтому числитель дроби равен 512 — 5 = 507. В периоде дроби стоят две цифры. Между запятой и первым периодом содержится одна цифра. Поэтому знаменатель дроби равен 990. Следовательно, получаем

Аналогично можно представить и другие десятичные дроби в виде обыкновенных дробей или смешанных чисел.

Пример 5

Представьте в виде смешанного числа дробь:

а) 1,(15);

б) 2,13(22).

Решение

По аналогии с примером 4 получаем

Наиболее часто в примерах используются конечные десятичные дроби. Поэтому рассмотрим правила действий с ними.

2. Действия над десятичными дробями

Сложение и вычитание десятичных дробей выполняют поразрядно. При этом дроби записывают одну под другой, чтобы запятая оказалась под запятой.

Пример 6

Выполните действия:

а) 2,136 + 1,24;

б) 2,136 - 1,24.

Решение

Умножение десятичных дробей нужно выполнять, не обращая внимания на запятые. Затем в полученном произведении надо отделить запятой справа столько цифр, сколько их стоит после запятой в обоих множителях вместе.

Пример 7

Перемножьте дроби 2,13 и 1,2.

Решение

Перемножим сначала натуральные числа 213 и 12.

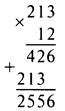
Теперь в полученном числе 2556 отделяем запятой три знака, так как в первом числе (2,13) после запятой два знака, а во втором числе (1,2) — один. Получаем число 2,556.

При делении десятичных дробей нужно в делимом и делителе перенести запятые вправо на столько цифр, сколько их стоит в делителе после запятой. Затем выполнить деление на натуральное число.

Пример 8

Разделите число 3,12 на: а) 2,4; б) 2,2.

Решение

а) Очевидно, что 3,12 : 2,4 = 31,2 : 24. Далее производим деление “уголком”.

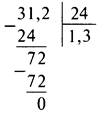
б) Очевидно, что 3,12 : 2,2 = 31,2 : 22. Далее производим деление “уголком”. В результате получаем число 1,4(18).

Обратите внимание на то, что сумма, разность, произведение конечных десятичных дробей также являются конечными десятичными дробями. Частное от деления конечных десятичных дробей может быть и конечной десятичной дробью (пример 8,а) и бесконечной периодической десятичной дробью (пример 8,б).

Операции над бесконечными периодическими десятичными дробями выполнить намного сложнее. Самый простой способ решения таких задач — перевести эти дроби в обыкновенные и выполнять действия над обыкновенными дробями.

Пример 9

Вычислите значение выражения 1,(3) - 0,(6) ∙ 1,(18).

Решение

Переведем бесконечные периодические десятичные дроби в обыкновенные:

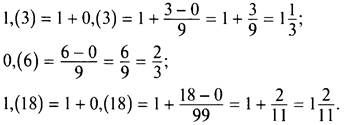
Теперь запишем тот же пример, но в виде обыкновенных дробей и выполним действия:

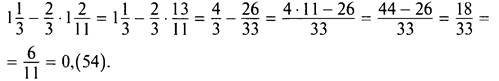
3. Порядок действий при вычислении значений выражений

1. Если выражение содержит скобки, то сначала выполняются все действия над числами, заключенными в скобках, а затем все остальные действия.

2. Сначала выполняют действия третьей ступени (возведение в степень), затем действия второй ступени (умножение и деление) и, наконец, действия первой ступени (сложение и вычитание). При этом действия одной и той же ступени выполняют в том порядке, в котором они записаны.

3. При вычислении дробного выражения выполняются действия в числителе и в знаменателе дроби и первый результат делится на второй.

Пример 10

Вычислите значение выражения:

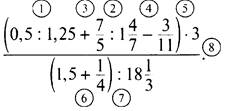
Решение

Порядок действий указан в примере (в соответствии с перечисленными правилами). Выполним эти действия.

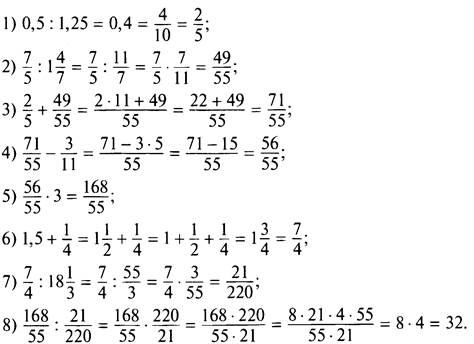
Итак, результатом выполненных действий является число 32.

Пример 11

Вычислите значение выражения:

Решение

Порядок действий указан в примере. Прежде всего, обратим бесконечные десятичные периодические дроби в обыкновенные. Получаем

Теперь запишем данный пример в виде обыкновенных дробей и выполним действия: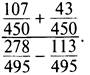

Итак, результатом выполненных действий является число 1.

4. Процент. Основные задачи на проценты

Процентом называют сотую часть любого числа или величины.

Пример 12

Найдите 1%: а) числа ; б) величины 5 ∙ а.

Решение

а) 1 % числа составляет число

б) 1% величины 5 ∙ а составляет величину

Задачи на проценты можно решать путем составления пропорции. Если принять целое (b) за 100%, а его часть (а) — за Р%, то получим пропорцию:

целое (b) — 100%;

часть (а) — Р%.

Отсюда получаем Из этого равенства можно выразить любую его составляющую.

Пример 13

Из группы туристов, состоящей из 80 человек, 20 туристов отправились на рыбалку. Сколько процентов туристов отправилось на рыбалку?

Решение

Так как целое b = 80 (человек), часть а = 20 (рыбаков), то Итак, на рыбалку отправилось 25% туристов.

Пример 14

При сушке фруктов испаряется 85% влаги. Сколько сухих фруктов получается из 200 кг свежих?

Решение

Так как при сушке испаряется 85% влаги, то в сухих фруктах сохраняется 100 - 85 = 15% массы свежих фруктов. Таким образом, надо найти часть а (масса сухих фруктов), если известно целое b (масса свежих фруктов) и Р = 15%. Из соотношения выразим:

Итак, из 200 кг свежих фруктов получается 30 кг сухих.

Пример 15

За первый день рабочий сделал 18 деталей, что составляет 20% всего задания. Сколько деталей должен сделать рабочий?

Решение

Надо найти целое (b), если известны часть (а = 18) и Р = 20%. Из равенства выразим: (деталей).

Итак, рабочий должен сделать 90 деталей.

IV. Задания на уроке

№ 1 (а, в, д, ж, и), 5 (б, г, е, ж), 7 (а, б), 17 (а, в).

V. Контрольные вопросы

— Запишите в виде десятичных дробей:

— Запишите в виде обыкновенных дробей или смешанных чисел: 0,36; 0,125; 5,015; 0,(3); 2,(63); 5,6(21).

— Как конечные десятичные дроби складываются (вычитаются, умножаются, делятся)? Какая десятичная дробь (конечная или бесконечная периодическая) будет результатом этих действий?

— Как выполнять действия над бесконечными периодическими десятичными дробями?

— Что называется процентом числа или величины?

— Как найти, сколько процентов Р составляет число а от числа b?

VI. Творческие задания

1. Зарплата увеличилась сначала на 10%, а затем еще на 20%. На сколько процентов увеличилась зарплата по сравнению с первоначальной?

Решение

Пусть сначала зарплата составляла 100 у. е. Так как 1% величины 100 у. е. равен сотой части, т. е. то 10% составляют величину, в 10 раз большую, т. е. 1 ∙ 10 = 10 (у. е).

Следовательно, после первого повышения зарплата составляет 100 + 10 = 110 (у. е.).

Рассмотрим второе повышение зарплаты. Так как 1% новой зарплаты в 110 у. е. равен сотой части, т. е. то 20% составляют величину, в 20 раз большую, т. е. 1,1 ∙ 20 = 22 (у. е.).

Следовательно, после второго повышения зарплата составляет 110 + 22 = 132 (у. е.).

По сравнению с первоначальной зарплата увеличилась на 132 - 100 = 32 (у. е.), что составляет от нее Таким образом, зарплата увеличилась на 32%.

Разумеется, вместо зарплаты, составляющей 100 у. е., можно было рассмотреть зарплату, составляющую а у. е. Легко убедиться, что процентное увеличение зарплаты не зависит от величины а.

2. Что больше — а% от числа b или b% от числа а?

Решение

Так как 1% от числа b равен b/100, то а% от этого числа составляют Так как 1% от числа а равен a/100, то b% от этого числа составляют Очевидно, что

Следовательно, а% от числа b равны b% от числа а.

3. Двое рабочих получали одинаковую зарплату. Зарплату первого рабочего сначала увеличили на 20%, а затем понизили на 20%. Зарплату второго рабочего, наоборот, сначала понизили на 20%, а затем увеличили на 20%. Какой рабочий стал получать больше? Как изменилась его зарплата по сравнению с первоначальной?

Решение

Пусть первоначально каждый из рабочих получал а у. е. Рассмотрим изменение зарплат рабочих.

Зарплата первого рабочего сначала увеличилась на 20%, т. е. на В результате зарплата равна Затем эта зарплата уменьшилась на 20%, т. е. на В итоге зарплата первого рабочего составляет

Зарплата второго рабочего сначала уменьшилась на 20%, т. е. на В результате зарплата равна Затем эта зарплата увеличилась на 20%, т. е. на В итоге зарплата второго рабочего

Видно, что зарплаты рабочих стали одинаковыми и уменьшились по сравнению с первоначальной на Эта величина составляет от первоначальной, т. е. уменьшилась на 4%.

4. В первом бруске массой 10 кг содержится 50% меди, а во втором бруске массой 5 кг — 80% меди. Бруски сплавили. Сколько процентов меди содержится в новом сплаве?

Решение

Найдем 1% массы первого бруска: Тогда масса меди в первом бруске составляет 0,1 ∙ 50 = 5 (кг).

Найдем 1% массы второго бруска: Тогда масса меди во втором бруске составляет 0,05 ∙ 80 = 4 (кг).

Масса меди в новом сплаве составляет 5 + 4 = 9 (кг) (так как медь в него попадет из первого и второго брусков). Масса нового сплава равна сумме масс первого и второго брусков, т. е. 10 + 5 = 15 (кг).

Тогда в новом сплаве содержится

VII. Подведение итогов урока

Домашнее задание

№ 1 (б, г, е, з), 2, 3, 7 (в, г), 8, 17 (б, д).