Поурочные разработки по алгебре 7 класс - к учебнику Ю.Н. Макарычева - 2014 год
Зачет по теме Формулы сокращенного умножения - ПРЕОБРАЗОВАНИЕ ЦЕЛЫХ ВЫРАЖЕНИЙ - ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
Цели: сравнить успеваемость учащихся при одинаковой сложности заданий; иметь возможность повысить оценки за выполненные контрольные работы.
Тип уроков: уроки контроля, оценки и коррекции знаний.
Ход уроков
I. Сообщение темы и целей уроков
II. Общая характеристика зачетной работы
Работа составлена в двух равноценных вариантах. По сравнению с контрольной работой увеличено количество заданий. Соответственно, у учащихся возрастает возможность выбора задач. Все задания разбиты на три блока А, В и С. Самые простые задачи представлены в блоке А, более сложные — в блоке В, еще сложнее — в блоке С. Каждая задача из блока А оценивается 1 баллом, из блока В — 2 баллами, из блока С — 3 баллами. Поэтому за правильное решение всех задач блока А можно получить 7 баллов, блока В - 8 баллов и блока С — 9 баллов (всего 24 балла). Оценка “3” ставится за 6 баллов, оценка “4” — за 10 баллов, оценка “5” — за 14 баллов.
Так как эта работа является зачетной, то в нее не включены принципиально новые задачи. Работа рассчитана на два урока.
III. Зачетная работа
Вариант 1
А
1. Преобразуйте в многочлен стандартного вида выражение:
2. Разложите на множители многочлен:
3. Упростите выражение 
4. Докажите, что число 1873 - 59 кратно 62.
5. Сравните числа (197 + 361)2 и 1972 + 3612.
6. Докажите, что при всех значениях х значение выражения 7 - 4х + 4x2 больше 5.
7. Постройте график функции у = (х + 2)2 - 4(х + 1).
В
8. Преобразуйте в произведение выражение 
9. Вычислите без калькулятора: 
10. Найдите наименьшее значение выражения 2а2 - 4ab + 4b2 - 2а + 4. При каких значениях а и b оно достигается?
11. Решите уравнение (3х - 2а)2 = (2х + а)2.
С
12. Сравните числа 
13. При каких значениях а равенство (х + 7)2 - 9(х + 5) + 2 = (х + 2)(х + а) является тождеством?
14. Постройте график функции 
Вариант 2
А
1. Преобразуйте в многочлен стандартного вида выражение:
2. Разложите на множители многочлен:
3. Упростите выражение 3(а + b)2 - (2а + b)(2a - b).
4. Докажите, что число 1173 - 49 кратно 53.
5. Сравните числа (341 + 113)2 и 3412 + 1132.
6. Докажите, что при всех значениях х значение выражения 5 - 6х + 9х2 больше 3.
7. Постройте график функции у = (х - 3)2 + 6(х - 1,5).
В
8. Преобразуйте в произведение выражение 
9. Вычислите без калькулятора: 
10. Найдите наименьшее значение выражения 10а2 - 6аb + b2 - 4а + 6. При каких значениях а и b оно достигается?
11. Решите уравнение (3х - 4а)2 - (х + 2а)2.
С
12. Сравните числа 
13. При каких значениях а равенство (х + 5)2 - 4(х + 1) + 11 = (х + 2)(х + а) является тождеством?
14. Постройте график функции 
IV. Разбор задач (ответы и решения)
Вариант 1
А
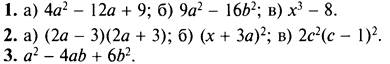
4. Доказано.
5. Первое число больше.
6. Доказано.
7. Парабола у = х2.
В
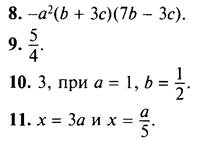
12. Для сравнения чисел преобразуем первое число. Каждый множитель в нем запишем, используя число 192. Получаем 
Изменим порядок умножения чисел и используем формулу разности квадратов: 
В этом произведении каждый множитель меньше 1922. Поэтому произведение меньше 1922 ∙ 1922 = 1924. Итак, первое число меньше второго.
(Ответ: первое число меньше.)
13. Используя формулу квадрата суммы, преобразуем данное равенство. Получаем 
или 
Приведем подобные члены и получим: 5х + 6 = ах + 2х + 2а или 3х + 6 = ах + 2а.
В левой и правой частях равенства стоят многочлены первой степени. Они будут тождественно равны, если коэффициенты при х в них одинаковы и свободные члены равны. Получаем условия: 3 = а и 6 = 2а, которые выполняются только при а = 3. Итак, при а = 3 данное равенство является тождеством.
(Ответ: а = 3.)
14. Преобразуем данную функцию 
Учтем, что |х| - 2 ≠ 0, т. е. х ≠ ±2. Используем свойство модуля х2 = |х|2 и формулу разности квадратов. Тогда можно сократить дробь.
Получаем 
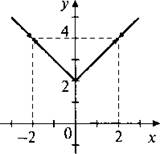
Построим график функции 
Из этого графика удалим две точки с абсциссами х ≠ ±2 (показаны стрелками).
Вариант 2
А
4. Доказано.
5. Первое число больше.
6. Доказано.
7. Парабола у = х2.
В
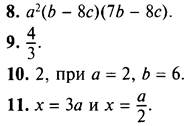
С
12. Для сравнения чисел преобразуем первое число. Каждый множитель в нем запишем, используя число 276. Получаем 
Изменим порядок умножения чисел и используем формулу разности квадратов: 
В этом произведении каждый множитель меньше 2762. Поэтому произведение меньше 2762 ∙ 2762 = 2764. Итак, первое число меньше второго.
(Ответ: первое число меньше.)
13. Используя формулу квадрата суммы, преобразуем данное равенство. Получаем 
или 
Приведем подобные члены и получим 6x + 8 = ах + 2х + 2а или 4x + 8 = ах + 2а.
В левой и правой частях равенства стоят многочлены первой степени. Они будут тождественно равны, если коэффициенты при х в них одинаковы и свободные члены равны. Получаем условия: 4 = а и 8 = 2а, которые выполняются только при а = 4. Итак, при а = 4 данное равенство является тождеством.
(Ответ: а - 4.)
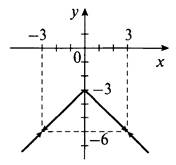
14. Преобразуем данную функцию 
Учтем, что |х| - 3 ≠ 0, т. е. х ≠ ±3. Используем свойство модуля х2 = |х|2 и формулу разности квадратов. Тогда можно сократить дробь. Получаем 
Построим график функции 
Из этого графика удалим две точки с абсциссами x ≠ ±3 (показаны стрелками).
V. Подведение итогов уроков