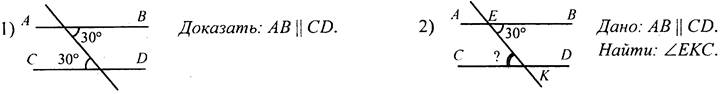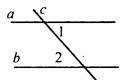СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ - ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ

Цель деятельности учителя

Создать условия для рассмотрения свойств параллельных прямых, демонстрации применения свойств параллельных прямых, закрепления знаний, умений, навыков учащихся по теме “Аксиома параллельных прямых”

Термины и понятия

Параллельные прямые, аксиома, свойства параллельных прямых

Планируемые результаты

Предметные умения

Универсальные учебные действия

Владеют геометрическим языком, умеют его использовать для описания предметов окружающего мира, владеют достаточно высоким уровнем развития пространственных представлений и изобразительных умений, навыков геометрических построений

Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев.

Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки.

Коммуникативные: считаются с разными мнениями и стремятся к координации различных позиций в сотрудничестве; подбирают аргументы для доказательства своей позиции, формулируют выводы.

Личностные: имеют целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И)

Образовательные ресурсы

• Тест.

• Таблица

I этап. Актуализация опорных знаний учащихся

Цель деятельности

Совместная деятельность

Систематизировать теоретический материал

(Ф/И)

1. Ответить на вопросы учащихся по домашнему заданию.

2. Тест с последующей самопроверкой (см. Ресурсный материал). (Задания 1 и 2 выполняются одновременно; 3 ученика работают у доски, остальные в тетрадях.)

II этап. Учебно-познавательная деятельность

Цель деятельности

Совместная деятельность

Ввести свойства параллельных прямых

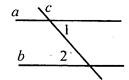
(Ф/И)

1. Решение задач.

Следует обратить внимание учащихся, что в первой задаче а || b по первому признаку параллельности прямых, а вторая задача является обратной первой, и в этом случае мы не знаем, равны ли накрест лежащие углы, если прямые параллельны. Таким образом, перед учащимися поставлена проблема, которую необходимо разрешить.

Условие. Пусть а || b, с - их секущая, ∠1 и ∠2 - накрест лежащие углы, образованные данными прямыми. Требуется выяснить, равны ли ∠1 и ∠2.

Решение этой задачи можно построить так же, как доказательство свойства накрест лежащих углов при параллельных прямых и их секущей по учебнику.

Вывод. Если две параллельные прямые пересечены третьей, то накрест лежащие углы равны.

- Это утверждение называют свойством накрест лежащих углов при параллельных прямых и их секущей.

2. Информация для учащихся.

- Во всякой теореме различают две части: условие и заключение. Условие теоремы - это то, что дано, а заключение - то, что требуется доказать.

Вывод. Теоремой, обратной данной, называется такая теорема, в которой условием является заключение данной теоремы, а заключением - условие данной теоремы.

3. Беседа о методе доказательства от противного по учебнику.

4. Доказательства следствия свойства накрест лежащих углов при параллельных прямых и их секущей и свойств соответственных и односторонних углов при параллельных прямых и их секущей.

Можно предложить учащимся провести доказательства самостоятельно в ходе выполнения упражнений.

- Докажите, что если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и другой.

- Сформулируйте теорему, обратную признаку параллельности прямых, использующему соответственные углы. Дайте название полученной теореме и докажите ее.

- Сформулируйте теорему, обратную признаку параллельности прямых, использующему односторонние углы. Дайте название полученной теореме и докажите ее.

- Заполните таблицу.

Название теоремы

Признак параллельности прямых

Свойство параллельности прямых

Формулировка теоремы

Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны

Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны

Условие(дано)

Прямые а, b; с - их секущая; ∠1, ∠2 – накрест лежащие углы; ∠1 = ∠2

Прямые а, b; с - их секущая; ∠1, ∠2 — накрест лежащие углы; а || b

Заключение (доказать)

а || b

∠1 = ∠2

- В чем заключается разница между этими теоремами?

III этап. Решение задач

Цель деятельности

Совместная деятельность

На простейших задачах отработать умение применять свойства параллельных прямых

(Ф/И)

Устно решить № 201, 205 по рисунку 117 и № 209 по рисунку 118

IV этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Перечислите свойства параллельных прямых.

- Что такое доказательство методом от противного?

- Оцените свою деятельность на уроке

(И) Домашнее задание: изучить п. 29; повторить пункты 15-28; ответить на вопросы 1-15 на с. 66-67 учебника; решить задачи № 202, 212