ОБ АКСИОМАХ ГЕОМЕТРИИ. АКСИОМА ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ - ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ

Цель деятельности учителя

Создать условия для формирования представления об аксиомах геометрии, введения аксиомы параллельных прямых и следствия из нее

Термины и понятия

Параллельные прямые, аксиома

Планируемые результаты

Предметные умения

Универсальные учебные действия

Владеют геометрическим языком, умеют его использовать для описания предметов окружающего мира, имеют пространственные представления и достаточно высокий

Познавательные: умеют адекватно оценивать правильность или ошибочность выполнения учебной задачи.

Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки.

Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками, разрешать конфликты на основе согласования интересов.

Личностные: проявляют целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И)

Образовательные ресурсы

• Задания для фронтальной работы.

• Историческая справка об аксиоме параллельных прямых

I этап. Актуализация опорных знаний

Цель деятельности

Совместная деятельность

Проанализировать ошибки, допущенные в самостоятельной работе

(Ф/И)

1. Сообщить результаты самостоятельной работы.

2. Проверить правильность выполнения домашнего задания

II этап. Беседа по новой теме

Цель деятельности

Совместная деятельность

Ввести понятие аксиомы, рассмотреть аксиому параллельных прямых

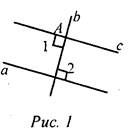
(Ф/И)

1. Беседа об аксиомах геометрии (см. пункт 27 и приложение 1 учебника).

2. Самостоятельное решение задачи с последующим обсуждением.

Задание: Через точку А, не лежащую на прямой а, провести прямую, параллельную прямой а.

Ход построения (рис. 1):

1) провести через точку А прямую b так, что a ⊥ b;

2) провести через точку А прямую с так, что b ⊥ с.

Доказательство: ∠1 = ∠2 = 90°, то есть накрест лежащие углы при прямых a и с и секущей b равны, следовательно, а || с.

Вопросы учащимся:

1) Всегда ли через точку, не лежащую на данной прямой, можно провести прямую, параллельную данной?

2) Сколько прямых, параллельных данной, можно провести через точку, не лежащую на данной прямой?

3) Можно ли доказать, что через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной?

- Математики с древних времен пытались доказать данное утверждение. В “Началах” Евклида оно называется пятым постулатом. Попытки доказать пятый постулат Евклида не увенчались успехом, и лишь в XIX веке было окончательно выяснено, что утверждение о единственности прямой, проходящей через данную точку параллельно данной прямой, не может быть доказано на основе остальных аксиом Евклида, а само является аксиомой. Огромную роль в решении этого вопроса сыграл русский математик Николай Иванович Лобачевский. Итак, аксиома параллельных прямых гласит: “Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной”.

- Является ли утверждение “Через точку, не лежащую на данной прямой, можно провести прямую, параллельную данной” аксиомой? Почему? (Это утверждение не является аксиомой, так как оно доказывается.)

- Чем отличаются вышеуказанные утверждения? (Аксиома параллельных прямых говорит о единственности такой прямой, а другое утверждение - о существовании такой прямой.)

III этап. Закрепление изученного материала

Цель деятельности

Деятельность учителя

Деятельность учащихся

Совершенствовать навыки решения простейших задач

(Ф/И) Организует деятельность учащихся.

1. Решить задачи № 196, 197 (устно).

Указание: при решении задачи № 197 полезно показать учащимся на рисунке два возможных случая расположения прямых:

1) все четыре прямые пересекают прямую р;

2) одна из четырех прямых параллельна прямой р, а три другие прямые пересекают ее.

Эти два случая иллюстрируют ответ на вопрос задачи: по крайней мере, три прямые пересекают прямую р.

2. Разъяснить смысл понятия “следствия”. Записать в тетрадях: “Следствиями называются утверждения, которые выводятся непосредственно из аксиом или теорем”,

3. Рассмотреть следствия 1 и 2 из аксиомы параллельных прямых.

4. Решить задачи № 198, 200, 218.

5. Решить задачу № 219

№ 218.

Дано: а ∩ b = А.

Можно ли построить прямую с, такую, что:

1) а || с; 2) с ∩ b?

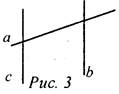
Доказательство:

Возьмем любую точку М ∉ а. По аксиоме параллельных прямых, через точку М можно построить прямую с, параллельную а, и притом только одну. Так как а || с, а ∩ b, тогда с ∩ b. Значит, можно построить такую прямую, параллельную прямой а и пересекающую прямую b.

№ 219.

Дано: с ∩ а, с ∩ b, с – любая.

Доказать: а || b.

Доказательство:

Пусть Проведем прямую с || b; с ∩ а, но (па построению), а это противоречит условию. Следовательно, a || b, что и требовалось доказать

IV этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Что нового узнали на уроке?

- В чем заключается аксиома Евклида?

- Составьте синквейн к уроку

(И) Домашнее задание: изучить пункты 27 и 28; ответить на вопросы 7-11 на с. 66-67 учебника; решить задачи № 217, 199