Геометрия 7 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015 год
НЕРАВЕНСТВО ТРЕУГОЛЬНИКА - СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА
|
Цель деятельности учителя |
Создать условия для доказательства теоремы о неравенстве треугольника, для обучения решению задач с опорой на изученные теоремы и следствия из них; способствовать развитию логического мышления учащихся |
|||
|
Термины и понятия |
Треугольник, противолежащий угол, сторона, неравенство треугольника |
|||
|
Планируемые результаты |
||||
|
Предметные умения |
Универсальные учебные действия |
|||
|
Владеют базовым понятийным аппаратом по основным разделам изучаемых понятий |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев; умеют устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение. Регулятивные: принимают и сохраняют цели и задачи учебной деятельности. Коммуникативные: умеют работать в сотрудничестве с учителем, аргументировать и отстаивать свою точку зрения. Личностные: проявляют креативность мышления, инициативу, находчивость, активность при решении геометрических задач |
|||
|
Организация пространства |
||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|||
|
Образовательные ресурсы |
• Задания для фронтальной работы |
|||
|
I этап. Актуализация опорных знаний учащихся |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Систематизировать теоретический материал |
(Ф/И) 1. Проверка усвоения изученного на предыдущем уроке материала. Фронтальный опрос. 2. Двое учащихся записывают на доске решения задач домашнего задания для последующей проверки с классом |
|||
|
II этап. Изучение нового материала |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Доказать теорему о неравенстве треугольника |
(Ф/И) 1. Доказательство теоремы о неравенстве треугольника (проводится учителем). 2. Решение задачи № 251 (см. на с. 75 учебника). После этого записать в тетрадях вывод: Каждая сторона треугольника меньше суммы двух других сторон, но больше разности двух других сторон: b - с < а < b + с; а - с < b < а + с; а - b < с < а + b. 3. Решение задачи № 248 (устно) |
|||
|
III этап. Решение задач |
||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
||
|
Учить решать задачи, используя изученные теоремы и следствия из них |
(Ф/И) Организует деятельность учащихся. 1. Решить задачу № 249. 2. Решить задачу № 250 (а) (самостоятельно). 3. Решить задачу № 253 на доске и в тетрадях |
№ 249. Дано: ΔАВС, АВ = ВС, а = 25 см, b = 10 см. Найти: какая из сторон является основанием?
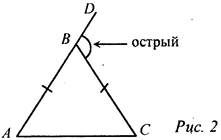
Решение: АС = 10 см, так как по неравенству треугольника АВ + ВС > АС, 25 + 25 > 10 - верно; если АС = 25 см, то АВ = ВС = 10, 10 + 10 > 25 - неверно. № 253. Дано: ΔABC, АВ = ВС, PАВC = 25 см, АС - АВ = 4 см, ∠DBC - острый. Найти: АВ, ВС, АС.
Решение: 1) Примем АВ = ВС = х см, следовательно, АС = x + 4 см. Так как РABC = АВ + ВС + АС, то 25 = х + х + х + 4; 21 = 3х; х = 7. АВ = ВС = 7 см, следовательно, АС = 11 см |
||
|
IV этап. Итоги урока. Рефлексия |
||||
|
Деятельность учителя |
Деятельность учащихся |
|||
|
(Ф/И) - При каком условии существует треугольник? - Составьте синквейн к уроку |
(И) Домашнее задание: выучить материал пунктов 30-34; ответить на вопросы 1-9 на с. 88; решить задачи № 242, 250 (б, в). |
|||