ДОПУСТИМЫЕ ЗНАЧЕНИЯ ПЕРЕМЕННЫХ, ВХОДЯЩИХ В ДРОБНОЕ ВЫРАЖЕНИЕ - РАЦИОНАЛЬНЫЕ ДРОБИ

Цель: формировать умение находить допустимые значения переменных, входящих в дробные выражения.

Ход урока

I. Организационный момент.

II. Устная работа.

Подставьте вместо значка * какое-нибудь число и назовите полученную дробь:

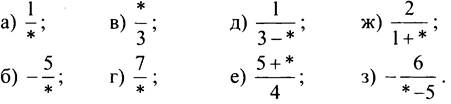
III. Объяснение нового материала.

1. Актуализация знаний учащихся.

- Какую дробь называют рациональной?

- Всякая ли дробь является дробным выражением?

- Как найти значение рациональной дроби при заданных значениях входящих в неё переменных?

2. Рассмотрение вопроса о том, всегда ли рациональная дробь имеет смысл.

Задание. Найдите значение дроби при указанных значениях переменной:

при х = 4; 0; 1.

Выполняя задание, учащиеся понимают, что при х = 1 невозможно найти значение дроби. Это позволяет им сделать следующий вывод: в рациональную дробь нельзя подставлять числа, которые обращают ее знаменатель в нуль (этот вывод должен быть сформулирован самими учащимися).

Далее учитель сообщает учащимся, что все значения переменных, при которых рациональное выражение имеет смысл, называют допустимыми значениями переменных.

3. Вывод правила нахождения допустимых значений переменных, входящих в рациональную дробь.

- Как находить допустимые значения переменных?

1) Если выражение является целым, то все значения входящих в него переменных будут допустимыми.

2) Чтобы найти допустимые значения переменных дробного выражения, нужно проверить, при каких значениях знаменатель обращается в нуль. Найденные числа не будут являться допустимыми значениями.

IV. Формирование умений и навыков.

• Выполнение заданий по учебнику: № 10, 11, 13, 14(а, в), 15 (г), 17.

Ответ на вопрос о допустимых значениях переменных, входящих в дробное выражение, может звучать по-разному. Например, рассматривая рациональную дробь можно сказать, что допустимыми значениями переменной являются все числа, кроме х = 4, или что в допустимые значения переменной не входит число 4, то есть х ≠ 4.

№ 11.

Ответ: x ≠ 0 и x ≠ 1 (или все числа, кроме 0 и - 1).

При выполнении заданий № 14 (а, в), 15 (г), 17 следует обратить внимание учащихся на необходимость учёта допустимых значений переменных.

№ 15.

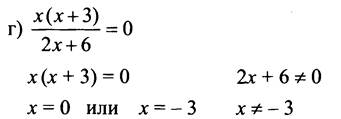
Ответ: х = 0.

• Дополнительные задания (для учащихся с высоким уровнем подготовки): № 18, 20.

№ 18.

Из всех дробей с одинаковым положительным числителем большей будет та, у которой знаменатель является наименьшим, то есть необходимо найти, при каком значении а выражение а² + 5 принимает наименьшее значение.

Поскольку выражение а² не может быть отрицательным ни при каких значениях а, то выражение а² + 5 будет принимать наименьшее значение при а = 0.

Ответ: а = 0.

Рассуждая аналогично, получим, что необходимо найти то значение а, при котором выражение (а - 3)² + 1 принимает наименьшее значение.

Ответ: а = 3.

№ 20.

Для ответа на вопрос предварительно нужно преобразовать выражение, стоящее в знаменателе дроби.

Дробь будет принимать наибольшее значение, если выражение (2x + у)² + 9 принимает наименьшее значение. Поскольку (2x + у)² не может принимать отрицательные значения, то наименьшее значение выражения (2х + у)² + 9 равно 9.

Тогда значение исходной дроби равно 18/9 = 2.

V. Итоги урока.

- Какие значения называются допустимыми значениями переменных, входящих в выражение?

- Каковы допустимые значения переменных целого выражения?

- Как найти допустимые значения переменных дробного выражения?

- Существуют ли рациональные дроби, для которых все значения переменных являются допустимыми? Приведите примеры таких дробей.

Домашнее задание: № 12, 14 (б, г), 212, 19 (дополнительно).