Алгебра поурочные планы 8 класс - по учебнику Ю. Н. Макарычева
МНОЖЕСТВО ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ - КВАДРАТНЫЕ КОРНИ
Цели: изучить множества иррациональных и действительных чисел; формировать умение различать эти множества чисел и сравнивать действительные числа.
Ход урока
I. Организационный момент.
II. Устная работа.
Определите, к какому множеству принадлежит каждое из чисел:
![]()
III. Объяснение нового материала.
1. Измерение длин отрезков на координатной прямой.
2. Постановка проблемной задачи: как измерить диагональ квадрата со стороной 1.
Обратимся к истории этого вопроса.
Математики Древней Греции более двадцати веков тому назад пришли к выводу, что нет ни целого, ни дробного числа, выражающего диагональ квадрата со стороной 1. Это вызвало кризис в математической науке: диагональ у квадрата есть, а длины у неё нет!
Математики нашли выход из этой ситуации: раз имеющегося запаса чисел - целых и дробных - не хватает для выражения длин отрезков, значит, нужны какие-то новые числа. Так появились иррациональные числа.
3. Введение множества действительных чисел.
- Что вам известно о различных множествах чисел?
На доску выносится рисунок:
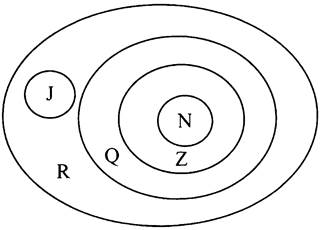
4. Сравнение иррациональных чисел с помощью различных примеров.
IV. Формирование умений и навыков.
Все задания можно разбить на две группы:
1-я группа. Задания на определение принадлежности чисел различным числовым множествам: № 276, 277, 279.
Пример выполнения задания.
Даны числа:
![]()
- Разделите их на две группы: рациональные и иррациональные.
- Заполните таблицу:
|
Натуральные числа |
Целые числа |
Рациональные числа |
Иррациональные числа |
2-я группа. Задания на сравнения действительных чисел: № 280, 281 (а, в, д), 285, 286.
V. Итоги урока.
- Какие числа называются рациональными, иррациональными?
- Из каких чисел состоит множество действительных чисел?
Домашнее задание: № 278, 281 (б, г, е), 282.