Алгебра поурочные планы 8 класс - по учебнику Ю. Н. Макарычева
РАЦИОНАЛЬНЫЕ ЧИСЛА - КВАДРАТНЫЕ КОРНИ
Цели: изучить множество рациональных чисел; формировать умение сравнивать рациональные числа и представлять их в виде бесконечных десятичных дробей.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Сравните числа:
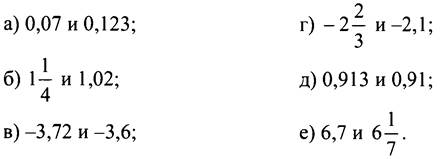
2. Переведите обыкновенную дробь в десятичную:
![]()
III. Объяснение нового материала.
1. Введение множества рациональных чисел
Рассмотрим, как происходит расширение числовых множеств от натуральных до рациональных чисел. Для наглядности на доске изобразим вложение одних множеств в другие.
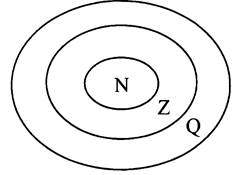
Задание. Определить, к какому множеству принадлежит каждое из чисел:
![]()
2. Представление рациональных чисел в виде обыкновенных дробей.
Любое рациональное число может быть представлено в виде дроби m/n (m є Z, n є N) различными способами.
3. Представление рациональных чисел в виде десятичных дробей.
Показать, как с помощью деления уголком любое рациональное число может быть представлено в виде конечной или бесконечной периодической десятичной дроби.
IV. Формирование умений и навыков.
• Выполнение заданий по учебнику: № 263, 264, 265, 267 (а, в, д, ж, и), 268 (а, в, д, ж), 269, 271.
V. Итоги урока.
- Принадлежит ли число - 2 множеству натуральных чисел? целых чисел? рациональных чисел?
- Какие числа составляют множество рациональных чисел?
- Сколькими способами можно представить рациональное число в виде обыкновенной дроби?
- Как представить рациональное число в виде десятичной дроби?
- Какая десятичная дробь может представлять рациональное число?
Домашнее задание: № 266, 267 (б, г, е, з, к), 268 (б, г, е, з), 270.