НАХОЖДЕНИЕ ПРИБЛИЖЕННЫХ ЗНАЧЕНИЙ КВАДРАТНОГО КОРНЯ С ПОМОЩЬЮ ОЦЕНКИ И НА КАЛЬКУЛЯТОРЕ - КВАДРАТНЫЕ КОРНИ

Цель: формировать умение находить приближенные значения квадратного корня при помощи оценки и на калькуляторе.

Ход урока

I. Организационный момент.

II. Устная работа.

Вычислите:

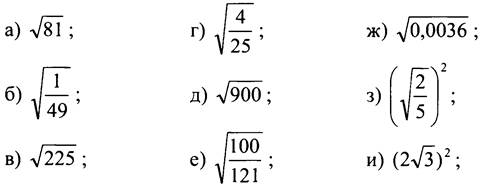
III. Объяснение нового материала по учебнику.

Сначала показать учащимся, как найти приближённое значение квадратного корня, оценивая его. При этом желательно привлекать учащихся к “открытию” этого способа. Затем попросить их сформулировать, как с помощью оценки может быть найдено приближённое значение любого квадратного корня.

Приведем несколько примеров, как применяется калькулятор для извлечения квадратных корней.

IV. Формирование умений и навыков.

• Все задания можно разбить на две группы:

1-я группа. Задания на нахождение приближенных значений квадратных корней с помощью оценки: № 336.

- Площадь квадрата равна 5 см². Чему равна его сторона? Дайте точный ответ, записав его с помощью знака √, и приближённый, выразив результат десятичной дробью с двумя знаками после запятой.

2-я группа. Задания на нахождение приближенных значений квадратных корней с помощью калькулятора: № 338 (б).

- С помощью калькулятора найдите значение √n для всех натуральных n от 1 до 10. Заполните таблицу, указывая приближённое значение √n с тремя знаками после запятой.

n	1	2	3	4	5	6	7	8	9	10
√n

Используя таблицу, сравните √6 и √3; √2 и √7; √10 и √8.

• Дополнительные задания: № 342, 343, 344 (а, в, д), 345, 347.

V. Тест с последующей проверкой.

“+” - согласен с утверждением;

“-” - не согласен с утверждением.

Утверждения:

1) √27 - это иррациональное число;

2) √64 - это иррациональное число;

3) √32 - это действительное число;

4) √81 - это действительное число;

5) √3 меньше 1;

6) √190 больше √160.

7) Любое иррациональное число заключено между двумя целыми числами;

8) Если число стоит под корнем, то оно иррациональное;

9) √7 меньше, чем -√10;

10) √59 заключено между числами 7 и 8.

Ключ:

1	2	3	4	5	6	7	8	9	10
+	-	+	+	-	+	+	-	-	+

VI. Итоги урока.

Учащиеся, сидящие за одной партой, обмениваются “ключами” к тесту. Учитель снова читает все десять утверждений, каждое из которых обсуждается. Одновременно учащиеся проверяют свои работы и ставят друг другу отметки по следующей шкале:

“5” - все ответы верные;

“4” - одна или две ошибки;

“3” - три или четыре ошибки;

“2” - более четырёх ошибок.

- Как найти приближённое значение квадратного корня с помощью метода оценки; с помощью калькулятора?

- Какое из чисел, √5 или √7, расположено левее на числовой оси? Почему?

Домашнее задание: № 337, 339, 334 (б, г, е), 346.