СОКРАЩЕНИЕ ДРОБЕЙ - РАЦИОНАЛЬНЫЕ ДРОБИ

Цель: формировать умение применять основное свойство дроби при сокращении дробей.

Ход урока

I. Организационный момент.

II. Устная работа.

Сократите дробь:

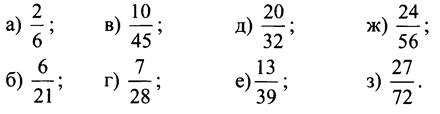
III. Объяснение нового материала.

1. Актуализация знаний и умений (учащиеся должны помнить формулы сокращенного умножения и основные приёмы разложения многочлена на множители).

- Какие существуют способы разложения многочлена на множители?

- В чём состоит каждый из этих способов?

- Разложите на множители многочлен:

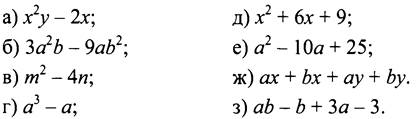
2. Разбор примера из учебника и формирование вывода: чтобы сократить рациональную дробь, нужно сначала разложить на множители её числитель и знаменатель.

IV. Формирование умений и навыков.

• Выполнение заданий по учебнику: № 29, 30 (а, в, д), 32 (а, в), 31, 34, 35 (а, в).

№ 35.

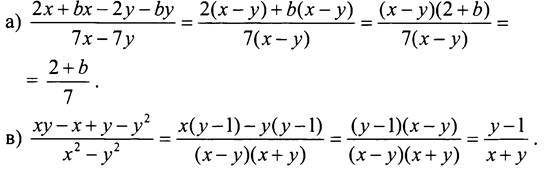
• Дополнительное задание.

№ 36.

Областью определения этой функции является множество всех чисел, кроме х = -5. Сократим дробь, задающую функцию:

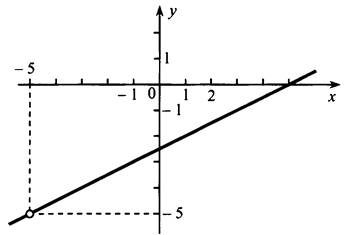
Графиком функции является прямая, а графиком функции - та же прямая, но с “выколотой” точкой (-5; -5).

V. Итоги урока.

- В чём состоит основное свойство дроби?

- Когда применяется основное свойство дроби?

- Что нужно сделать, чтобы сократить рациональную дробь?

- Какие существуют способы разложения многочлена на множители?

Домашнее задание: № 30 (б, г, е), 32 (б, г), 33, 35 (б, г), 36 (б) (дополнительно).