ПРИМЕНЕНИЕ ТЕОРЕМЫ ВИЕТА И ОБРАТНОЙ ЕЙ ТЕОРЕМЫ - КВАДРАТНЫЕ УРАВНЕНИЯ

Цель: продолжить формирование умения применять теорему Виета и обратную ей теорему при решении приведённых и неприведённых квадратных уравнений.

Ход урока

I. Организационный момент.

II. Устная работа.

Убедитесь, что уравнение имеет корни, и назовите их сумму и произведение:

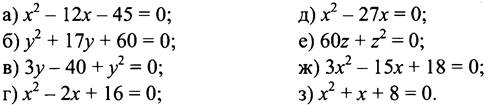
III. Проверочная работа.

Вариант 1

1. Зная один из корней уравнения, найдите другой корень, используя теорему Виета:

2. Какое число надо подставить вместо а, чтобы корнями уравнения х² -ах + 6 = 0 были бы числа 2 и 3?

Вариант 2

1. Зная один из корней уравнения, найдите другой корень, используя теорему Виета:

2. Какое число надо подставить вместо а, чтобы корнями уравнения х² - 5х + а = 0 были бы числа 2 и 3?

IV. Формирование умений и навыков.

На этом уроке учащиеся решают приведённые и неприведённые квадратные уравнения с помощью теоремы, обратной теореме Виета.

На первых порах учащимся может быть трудно подбирать корни устно, поэтому стоит предложить им обозначать корни уравнения и записывать соответствующие равенства.

Обратить внимание учащихся, что подбор корней начинаем с оценивания произведения корней, то есть находим делители свободного члена квадратного уравнения.

• Выполнение заданий по учебнику.

№ 586.

Пусть х₁ = 12,5 и х₂ - корни уравнения х² – 13х + q = 0, тогда х₁ + х₂ = 13 и х₁ ∙ х₂ = q.

Имеем 12,5 + х₂ = 13, значит, х₂ = 13 - 12,5, х₂ = 0,5.

Тогда 12,5 ∙ 0,5 = q, q = 25.

Ответ: х₂ = 0,5; q = 25.

№ 587.

Пусть х₁ = 8 и х₂ - корни уравнения 5х² + bх + 24 = 0, тогда

Имеем значит,

Тогда

Ответ: х₂ = 0,6; b = -43.

№ 589, 590 (самостоятельно).

№ 593 (а), 594 (а, д, е), 595 (б, д, е), 675.

После выполнения задания № 675 можно рассмотреть с учащимися два способа нахождения корней квадратного уравнения, вытекающие из теоремы Виета.

1-й способ. Если в квадратном уравнении ах² + bх + с = 0 сумма коэффициентов равна нулю, то

2-й способ. Если в квадратном уравнении ах² + bх + с = 0 сумма коэффициентов а и с равна коэффициенту b, то х₁ = -1, x₂ = -c/a.

В буквенном виде это может быть записано так:

ах2 + bх + с = 0
Если а + b + с = 0, то	Если а + с = b, то

• Дополнительное задание повышенной трудности.

№ 591.

Пусть х₁, x₂ - корни уравнения х² + 2х + q = 0.

По теореме Виета х₁ + х₂ = - 2 (1) и х₁ ∙ x₂ = q(2).

По условию (через х₁ обозначим больший корень). Значит, по формуле сокращенного умножения

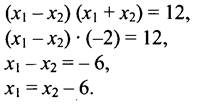
Подставим в первое равенство вместо x₁ его значение:

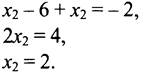
Вычислим x₁ = 2 - 6 = -4.

Из второго равенства найдём g = -4 ∙ 2, q = 8.

Ответ: q = 8.

V. Итоги урока.

- Сформулируйте теорему Виета и обратную ей теорему. -Если коэффициент с квадратного уравнения является положительным числом, то какими по знаку могут быть его корни? А если с - отрицательное число?

- Какие корни имеет квадратное уравнение, если сумма его коэффициентов равна нулю? А если а + с = b?

Домашнее задание: № 585, 588, 594 (б, в, г), 595 (а, в, г), 592*.