КОНТРОЛЬНАЯ РАБОТА 6 - КВАДРАТНЫЕ УРАВНЕНИЯ

Вариант 1

1. Решите уравнение:

2. Из пункта А в пункт В велосипедист проехал по одной дороге длиной 27 км, а обратно возвращался по другой дороге, которая была короче первой на 7 км. Хотя на обратном пути велосипедист уменьшил скорость на 3 км/ч, он все же на обратный путь затратил времени на 10 минут меньше, чем на путь из А в В. С какой скоростью ехал велосипедист из А в В?

Вариант 2

1. Решите уравнение:

2. Катер прошёл 12 км против течения реки и 5 км по течению. При этом он затратил столько времени, сколько ему потребовалось бы, если бы он шёл 18 км по озеру. Какова собственная скорость катера, если известно, что скорость течения реки равна 3 км/ч?

Вариант 3

1. Решите уравнение:

2. Из пункта А в пункт В велосипедист проехал по дороге длиной 48 км, обратно он возвращался по другой дороге, которая короче первой на 8 км. Увеличив на обратном пути скорость на 4 км/ч, велосипедист затратил на 1 час меньше, чем на путь из А в В. С какой скоростью ехал велосипедист из пункта А в пункт В?

Вариант 4

1. Решите уравнение:

2. Катер прошёл 15 км против течения и 6 км по течению, затратив на весь путь столько же времени, сколько ему потребовалось бы, если бы он шёл 22 км по озеру. Какова собственная скорость катера, если известно, что скорость течения реки равна 2 км/ч?

Решение вариантов контрольной работы

Вариант 1

Общий знаменатель х² - 9.

По теореме, обратной теореме Виета, x₁ = 3; х₂ = -4.

Если х = 3, то х² - 9 = 0.

Если х = -4, то х² - 9 ≠ 0.

Общий знаменатель х (х - 2).

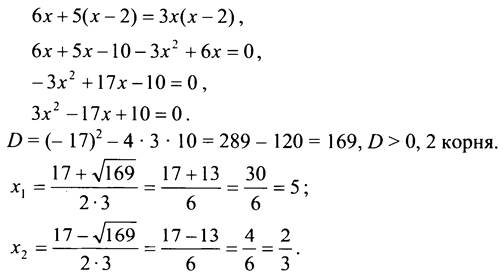
Если х = 5, то х(х - 2) ≠ 0.

Если х = 2/3, то х(х - 2) ≠ 0.

Ответ: а) -4; б) 2/3; 5.

2. Пусть х км/ч - скорость велосипедиста, с которой он ехал из А в В, тогда (х - 3) км/ч - скорость, с которой он ехал обратно. На путь из А в В он затратил 27/x ч, а обратно Зная, что на обратный путь он затратил на 10 мин (1/6 часа) меньше, составим уравнение:

Общий знаменатель 6х(х - 3).

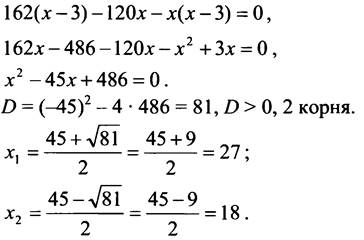
Ни один из корней не обращает знаменатель в нуль, но корень х = 27 не удовлетворяет условию задачи (слишком большая скорость для велосипедиста).

Ответ: 18 км/ч.

Вариант 2

Общий знаменатель х² - 16.

По теореме, обратной теореме Виета, х₁ = 4; х₂ = -1.

Если х = 4, то х² - 16 = 0.

Если х = -1, то х² - 16 ≠ 0.

Общий знаменатель х(х - 5).

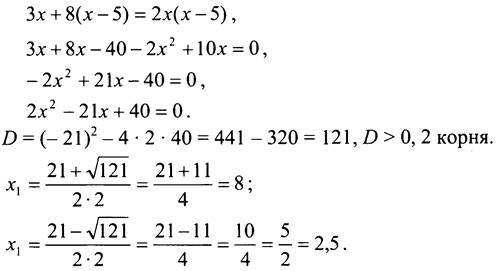
Если х = 8, то х(х - 5) ≠ 0.

Если х = 2,5, то х(х - 5) ≠ 0.

Ответ: а) -1; б) 2,5; 8.

2. Пусть х км/ч - собственная скорость катера, тогда против течения он шёл со скоростью (х - 3) км/ч, по течению - (х + 3) км/ч и по озеру - х км/ч. Против течения он шел по течению а по озеру он шел бы 18/x ч. Зная, что на все плавание по реке он затратил бы столько же времени, сколько на плавание по озеру, составим уравнение:

Общий знаменатель х(х - 3)(х + 3).

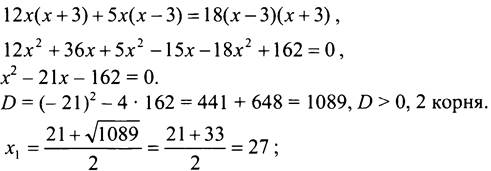
Ни один из корней не обращает знаменатель в нуль, но x = -6 не удовлетворяет условию задачи.

Ответ: 27 км/ч.

Вариант 3

Общий знаменатель x² - 1.

По теореме, обратной теореме Виета, х₁ = 5; x₂ = -1.

Если x = 5, то х² - 1 ≠ 0.

Если х = -1, то х² - 1 = 0.

Общий знаменатель x(x - 3).

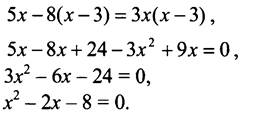
По теореме, обратной теореме Виета, х₁ = 4; x₂ = -2.

Если х = 4, то х(x - 3) ≠ 0.

Если x = -2, то х(x - 3) ≠ 0.

Ответ: а) 5; б) -2; 4.

2. Пусть х км/ч - скорость, с которой велосипедист ехал из А в В, тогда (x + 4) км/ч - скорость, с которой он ехал обратно. На путь из А в В он затратил 48/x ч, а обратно Зная, что на обратный путь он затратил на 1 ч меньше, составим уравнение:

Общий знаменатель х(х + 4).

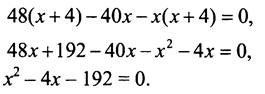
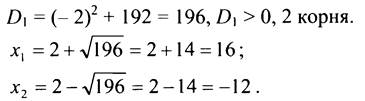
Ни один из корней не обращает знаменатель в нуль, но корень х = -12 не удовлетворяет условию задачи.

Ответ: 16 км/ч.

Вариант 4

Общий знаменатель х² - 4.

По теореме, обратной теореме Виета, x₁ = 7; х₂ = -2.

Если х = 7, то х² - 4 ≠ 0.

Если х = -2, то х² - 4 = 0.

Общий знаменатель х(х - 3).

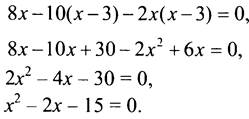
По теореме, обратной теореме Виета, x₁ = 5; х₂ = -3.

Если х = 5, то х(х - 3) ≠ 0.

Если х = -3, то х (х - 3) ≠ 0.

Ответ: а) 7; б) -3; 5.

2. Пусть х км/ч - собственная скорость катера, тогда против течения он шёл со скоростью (х - 2) км/ч, по течению - (х + 2) км/ч и по озеру - х км/ч. Против течения он шёл по течению а по озеру он шел бы 22/x ч. Зная, что на все плавание по реке он затратил бы столько же времени, сколько на плавание по озеру, составим уравнение:

Общий знаменатель х(х - 2)(х + 2).

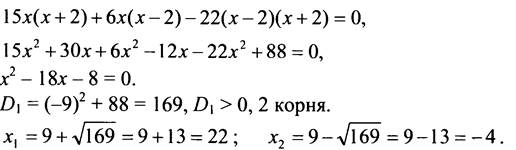
Ни один из корней не обращает знаменатель в нуль, но корень x = -4 не удовлетворяет условию задачи.

Ответ: 22 км/ч.