ТЕОРЕМЫ, ВЫРАЖАЮЩИЕ СВОЙСТВА ЧИСЛОВЫХ НЕРАВЕНСТВ - НЕРАВЕНСТВА

Цели: изучить теоремы, выражающие свойства числовых неравенств; формировать умение применять теоремы-свойства при решении задач.

Ход урока

I. Организационный момент.

II. Устная работа.

1. Сравните числа:

2. Не выполняя вычислений, сравните значения выражений:

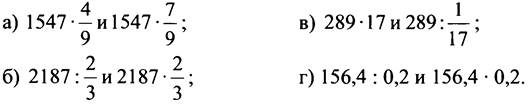
3. Сравните выражения:

III. Объяснение нового материала.

1. “Открытие” свойств числовых неравенств.

На этом этапе можно организовать работу учащихся в группах (лабораторная работа).

1-я группа - арифметический блок.

Задание 1. Сравните числа:

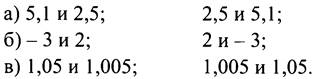
Вывод. Если а > b, то b ... а.

Если а < b, то b ... а.

Задание 2. Сравните числа:

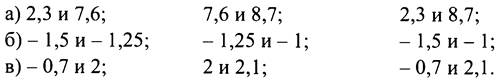
Вывод. Если а < b и b < с, то а ... с.

Задание 3. Сравните:

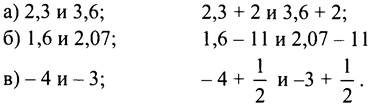
Вывод. Если а < b ,то а + с ... b + с.

Задание 4. Сравните:

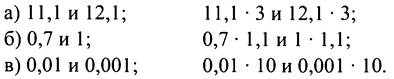
Вывод. Если а < b и с > 0, то ab ... bс.

Сравните:

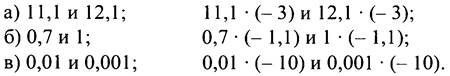
Вывод. Если а < b и с < 0, то ab ... bс.

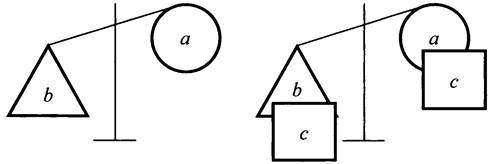
2-я группа - геометрический блок.

Задание 1. Если а правее Ь, то b ... а (а > b, то b ... а).

Задание 2. Если а левее b и b левее с, то а ... с.

Задание 3. Если а левее b и с - любое число, то а + с ... b + с.

Задание 4. Если а левее b и с - положительное число, то ас ... bс.

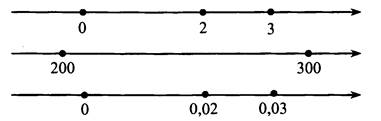
Используя рисунок, заполните пропуски так, чтобы получились верные утверждения.

Так как 2 < 3, то 2 ∙ 100 ... 3 ∙ 100.

Так как 2 < 3, то 2 ∙ 0,01 ... 3 ∙ 0,01.

3-я группа - практический блок.

Задание 1. Если а тяжелее b, то b ... а (а > b, то b ... а).

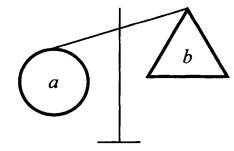
Задание 2. Если а легче b и b легче с, то а ... с.

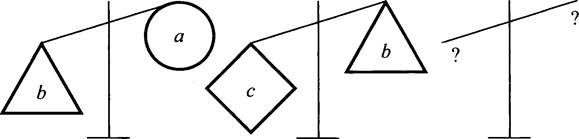
Задание 3. Если а легче b и с - любое число, то а + с ... b + с.

Задание 4. Если а легче b и с - положительное число, то ас ... bс.

2. Формулировка и доказательство теорем, выражающих свойства числовых неравенств.

Разобрать доказательство четырёх теорем согласно пункту учебника.

3. Прочитать правило (формулировка теоремы 4) на с. 158 учебника. Обратить внимание на важность знания этой теоремы для решения неравенств с одной переменной.

4. Рассмотреть на конкретном примере следствие из теоремы 4 на с. 158.

IV. Формирование умений и навыков.

• № 746, 748.

Эти задания на применение теорем 1 и 2. При решении следует выполнять как построение координатной прямой с точками (геометрическая интерпретация), так и запись соответствующих числовых неравенств.

• № 749 (а, в), 750 (б, г), 751 (а, в, е).

Примеры выполнения заданий:

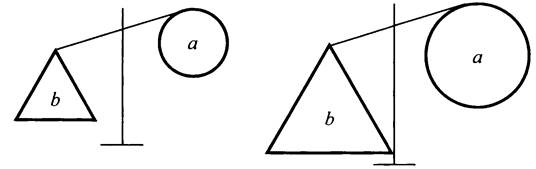
№ 749.

Значит, а и b - положительные числа.

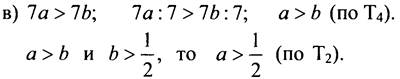
Значит, а и b - положительные числа.

№ 750.

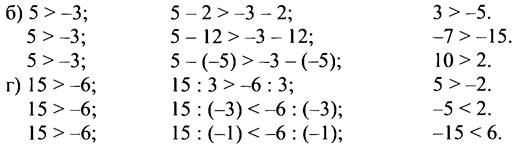
№ 751.

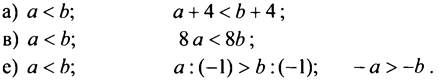
• № 752 (устно), 753 (устно).

V. Итоги урока.

- Сформулируйте основные свойства числовых неравенств.

- Если к обеим частям верного неравенства прибавить отрицательное число, то получится ли верное неравенство?

- Можно ли обе части верного неравенства домножить на отрицательное число, чтобы получилось верное неравенство? Какое ещё условие необходимо соблюсти?

- Если а < b и b > 4. Можно ли утверждать, что а > 4?

Домашнее задание: № 747, 749 (б, г), 750 (а, в), 751 (б, г, д), 764 (а, в).