ТЕОРЕМЫ О ПОЧЛЕННОМ СЛОЖЕНИИ И УМНОЖЕНИИ НЕРАВЕНСТВ - НЕРАВЕНСТВА

Цели: изучить формулировки и доказательства теорем о почленном сложении и умножении неравенств; формировать умение применять данные теоремы при решении задач.

Ход урока

I. Организационный момент.

II. Проверочная работа.

Вариант 1

1. Известно, что 10 < а < 16. Оцените значение выражения:

2. Известно, что 2,2 < √5 < 2,3. Оцените значение выражения:

Вариант 2

1. Известно, что 5 < m < 15. Оцените значение выражения:

2. Известно, что 2,6 < √7 < 2,7. Оцените значение выражения:

Вариант 3

1. Известно, что 15 < x < 20. Оцените значение выражения:

2. Известно, что 3,31 < √11 < 3,32. Оцените значение выражения:

Вариант 4

1. Известно, что 6 < у < 9. Оцените значение выражения:

2. Известно, что 4,12 < √13 < 4,13. Оцените значение выражения:

III. Объяснение нового материала.

1. Для мотивации изучения теорем о сложении и умножении числовых неравенств следует предложить учащимся для решения задачи практического характера.

Задача 1. Длина прямоугольника больше 12 см, а его ширина больше 3 см. Можно ли утверждать, что периметр этого прямоугольника больше 30 см?

Решение

Пусть а и b - длина и сторона прямоугольника соответственно, тогда периметр равен 2а + 2b.

Доказать, что 2а + 2b> 30.

Учащиеся могут интуитивно сложить почленно неравенства и получить следующий результат:

Следует отметить, что так можно поступать, но необходимо провести доказательство, используя известные теоремы, выражающие свойства числовых неравенств.

Из неравенств (1) и (2) по теореме 2 следует, что 2а + 2b > 30.

Далее просим учащихся сформулировать “открытое” ими утверждение в общем виде и записать его аналитическую модель:

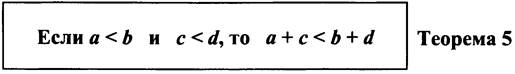
Доказательство теоремы можно разобрать по учебнику, так как в нём повторяется ход рассуждений для решения задачи 1.

Задача 2. Длина прямоугольника больше 15 дм, а его ширина больше 6 дм. Можно ли утверждать, что его площадь больше 90 дм²?

Решение

Можно предложить учащимся провести доказательство утверждения самостоятельно по аналогии с предыдущей задачей.

Пусть а и b - длина и сторона прямоугольника, тогда его площадь равна а ∙ b.

а > 15; b > 6.

Доказать, что ab > 90.

Из неравенств (1) и (2) по теореме 2 следует, что ab > 90.

Просим учащихся дать общую формулировку утверждения. Замечаем, что теорема о почленном умножении неравенств справедлива для положительных чисел. Если среди чисел есть отрицательные, то при почленном умножении неравенств может получиться неверное неравенство. Просим учащихся привести контрпримеры. На доску выносится запись:

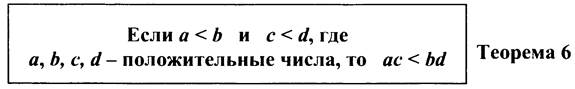
Доказательство разбираем по учебнику.

2. Следствие из теоремы 6 также разбираем по учебнику.

IV. Формирование умений и навыков.

Обращаем внимание учащихся, что для почленного сложения или умножения неравенств удобнее их записывать друг под другом.

• Выполнение заданий: № 765, 766, 767 (а), 768.

№ 767.

а) а¹ > b², значит,

а и b - положительные числа, значит, а + b > 0. Разделим обе части неравенства на а + b, получим а – b > 0, значит, а > b.

Имеем: а² > b²

то есть а³ > b³.

№ 768.

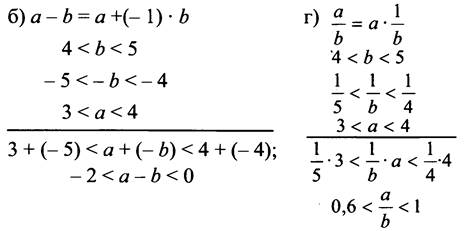
• Задание повышенной сложности на “прямое” применение теорем 5 и 6: № 776.

№ 776.

Запишем соотношение между средним арифметическим и средним геометрическим для всех пар чисел:

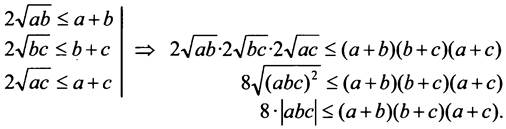
Так как значит, то есть

V. Итоги урока.

- Сформулируйте теорему о почленном сложении неравенств.

- Сформулируйте теорему о почленном умножении неравенств. Какие ограничения накладываются на числа?

- Сформулируйте следствие из теоремы о почленном умножении неравенств.

- Можно ли применить данные теоремы к более чем двум неравенствам указанного вида?

Домашнее задание: 1. № 767 (б), 769.

2. Докажите, что если а > 5 и b > 6, то

3. Докажите, что если а > 6 и b < -1,то

4. № 776 (б)* (дополнительное задание).