ИСПОЛЬЗОВАНИЕ ТЕОРЕМ О ПОЧЛЕННОМ УМНОЖЕНИИ И СЛОЖЕНИИ НЕРАВЕНСТВ ПРИ ОЦЕНКЕ ЗНАЧЕНИЯ ВЫРАЖЕНИЯ - НЕРАВЕНСТВА

Цели: закрепить знание теорем о почленном сложении и умножении неравенств; формировать умения применять данные теоремы для оценки значения выражения, решать задачи повышенной трудности.

Ход урока

I. Организационный момент.

II. Устная работа.

1. Известно, что -5 < а < 9. Оцените значение выражения:

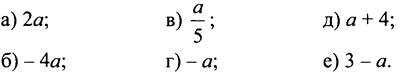
2. Пусть b - произвольное число, сравните с нулём значение выражения:

3. Известно, что х > 5, у > 15. Оцените значение выражения:

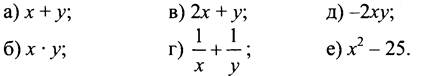
III. Формирование умений и навыков.

1. Актуализация знаний.

При выполнении устной работы учащиеся использовали теоремы о почленном сложении и умножении неравенств и следствие. Просим их сформулировать данные теоремы.

2. Работа по учебнику.

Теоремы о почленном сложении и умножении неравенств используются для оценки суммы, разности, произведения и частного. Разбираем примеры 1-4 на с. 162-163 учебника. Еще раз обращаем внимание на удобную запись неравенств (одного под другим) при выполнении почленного сложения либо умножения: № 770.

3. Задание. Докажите, что если 0 < a < 7 и 0 < b < 3, то

Доказательство

Так как 68 < 70, то 0 < 5а + 11b < 70.

Так как 25 < 30, то 4 < ab + 4 < 30.

4. В следующих заданиях демонстрируется практическое применение теорем о почленном сложении и умножении неравенств.

№ 772.

Пусть а - основание, b - боковая сторона равнобедренного треугольника, тогда Р = а + 2b - периметр этого треугольника.

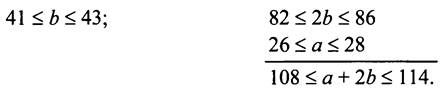
Ответ: 108 ≤ Р ≤ 114.

№ 774.

Пусть а и b - длина и ширина прямоугольной комнаты, тогда её площадь равна ab.

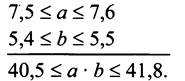
Так как требуется комната площадью не менее 40 м² (то есть S ≥ 40), то данное помещение подойдёт для библиотеки.

Ответ: да.

№ 775.

Пусть а, β - углы треугольника, тогда третий угол у, по теореме о сумме углов треугольника, равен 180 ° - а – β.

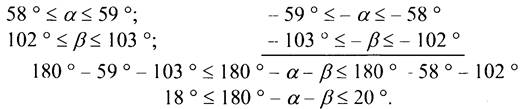
Ответ: 18° ≤ y ≤ 20°.

5. Задания повышенной трудности (для сильных учащихся).

№ 777.

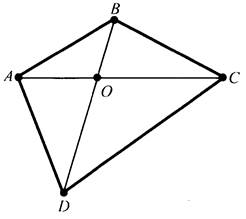
Пусть ABCD - выпуклый четырехугольник, тогда его диагонали пересекаются в точке О.

Докажем, что АВ + DC < АС + BD и ВС + AD < АС + BD.

Воспользуемся неравенством треугольника (каждая сторона треугольника меньше суммы двух других сторон).

№ 778.

Медианы треугольника АВС пересекаются в одной точке О. Обозначим длины сторон треугольника а, b, с. АА₁, ВВ₁, СС₁ - медианы.

1) Докажем, что сумма длин медиан треугольника больше его полупериметра.

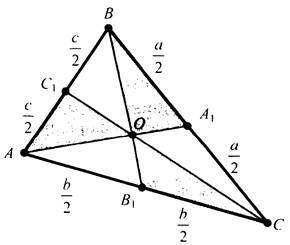
Воспользуемся неравенством треугольника:

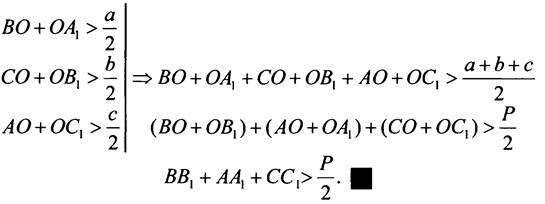
2) Докажем, что сумма длин медиан треугольника меньше его периметра.

Предлагаем учащимся решить самостоятельно это задание в классе или дома.

IV. Итоги урока.

- Сформулируйте основные свойства числовых неравенств.

- Сформулируйте теоремы о сложении и умножении числовых неравенств.

- Каким образом используют теоремы о сложении и умножении числовых неравенств при оценке значения выражения?

Домашнее задание: 1. № 771, 773.

2. Верно ли, что:

а) если а > 4 и b > 6, то 2а + b > 45;

б) если а > 3 и b > 9, то 3ab > 30.

3. Сравните, если возможно:

а) 3а + 2b и 16, если а > 4 и b > 8;

б) 5а - b и 20, если а > 4 и b < -3.

4. № 776 (б)*.