Геометрия 9 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015
УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО - ВЕКТОРЫ
|
Цель деятельности учителя |
Создать условия для введения понятия умножения вектора на число; для рассмотрения основных свойств умножения вектора на число |
||||
|
Термины и понятия |
Вектор, коллинеарные векторы, сонаправленные, противоположно направленные |
||||
|
Планируемые результаты |
|||||
|
Предметные умения |
Универсальные учебные действия |
||||
|
Умеют применять векторы, находить вектор, который больше или меньше данного вектора в несколько раз |
Познавательные: умеют создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных и познавательных задач. Регулятивные: умеют осуществлять контроль по результату и способу действий на уровне произвольного внимания и вносить необходимые коррективы. Коммуникативные: выстраивают аргументацию, участвуют в диалоге. Личностные: проявляют креативность мышления, инициативность, находчивость, активность при решении геометрических задач |
||||
|
Организация пространства |
|||||
|
Формы работы |
Фронтальная (Ф); парная (П); индивидуальная (И) |
||||
|
Образовательные ресурсы |
• Задача для парной работы; • задания для проверочной работы; • чертежи для задач |
||||
|
I этап. Мотивация к деятельности |
|||||
|
Цель деятельности |
Постановка учебной деятельности |
||||
|
Дать задачу, приводящую к формулировке новой темы |
Тему урока на доске можно не писать. После решения задачи учащиеся могут сами ее сформулировать. (П) Решите задачу. Лодка движется прямолинейно с некоторой скоростью |
||||
|
II этап. Учебно-познавательная деятельность |
|||||
|
Цель деятельности |
Совместная деятельность |
||||
|
Ввести понятие умножения ненулевого вектора на число |
(Ф) 1. Определение произведения вектора на число, его обозначение: 2. Запись в тетрадях: 1) произведение любого вектора на число нуль есть нулевой вектор; 2) для любого числа k и любого вектора 3. Основные свойства умножения вектора на число: Для любых чисел к, 1 и любых векторов
Примечание. Рассмотренные нами свойства действий над векторами позволяют в выражениях, содержащих суммы, разности векторов и произведения векторов на числа, выполнять преобразования по тем же правилам, что и в числовых выражениях. Например:
|
||||
|
III этап. Закрепление изученного материала. Решение задач |
|||||
|
Цель деятельности |
Совместная деятельность |
||||
|
Совершенствовать навыки решения задач |
(Ф/И) 1. Выполнить практические задания № 776 (б, г, д), 777. 2. Решить задачи № 779, 781 (а, в) на доске и в тетрадях. 3. Решить задачу № 780 (б) |
||||
|
IV этап. Решение задач |
|||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|||
|
Совершенствовать навыки решения задач |
(Ф/И) 1. Выполнить практическое задание № 756. 2. Решить задачу № 766 по рис. 259 (устно). 3. Решить задачу № 764 (а) на доске и в тетрадях. 4. Решить № 765 и 772. 5. Решить задачи по готовым чертежам:
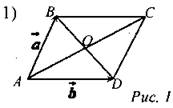
Дано: ABCD - параллелограмм, Выразить через
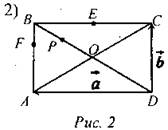
Дано: ABCD - прямоугольник, Выразить через
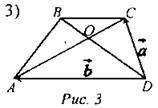
Дано: ABCD - трапеция. Выразить через 6. Решить задачу № 782 на доске и в тетрадях. 7. Решить задачу № 802 на доске и в тетрадях* |
№ 764. Решение:
Ответ: AK |
|||
|
V этап. Самостоятельная работа |
|||||
|
Цель деятельности |
Задания для самостоятельной работы |
||||
|
Проверить уровень усвоения материала |
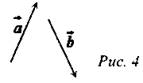
(И) Проверочная работа с самопроверкой. (Учитель заранее готовит правильные ответы.) 1) Построить:
2) Дан параллелограмм ABCD. Построить векторы: |
||||
|
VI этап. Итоги урока. Рефлексия |
|||||
|
Деятельность учителя |
Деятельность учащихся |
||||
|
(Ф/И) - Что нового узнали на уроке? - Сформулируйте три вопроса по уроку |
(И) Домашнее задание: повторить материал пунктов 76-83; ответить на вопросы 1-17, с. 208-209 учебника; решить задачи № 783, 804, 775, 776 (а, в, е), 781 (б), 780 (а) |
||||