Определение числовой функции. Область определения, область значений функции - Числовые функции

Понятие функции является основополагающим для всего курса алгебры. С функцией непосредственно связаны понятия уравнения, неравенства, системы уравнений, системы неравенств, последовательности и прогрессий. Поэтому необходимо обратить самое серьезное внимание на эту тему.

Уроки 32-33. Определение числовой функции. Область определения, область значений функции

Цель: уточнить понятие функции и ее основные характеристики: область определения и область значений.

Ход уроков

I. Сообщение темы и цели уроков

II. Изучение нового материала

С понятием функции школьники познакомились уже в 7 классе. Теперь необходимо уточнить и развить это понятие.

Определение 1. Пусть даны числовые множества X и Y. Если указано правило f, позволяющее поставить в соответствие каждому элементу х из X определенный элемент у из множества Y, то говорят, что задана функция у = f(x) с областью определения X и областью значений Y. При этом переменную x называют независимой переменной или аргументом, переменную у - зависимой переменной.

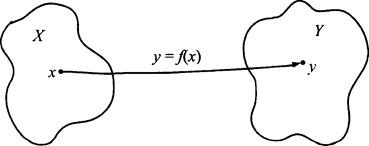
Для области определения функции у = f(х) принято обозначение D(f), для области значений - обозначение E(f).

Пример 1

Рассмотрим функцию Чтобы найти значение у для каждой величины х, надо выполнить следующие действия (операции):

1) из величины х вычесть число 3 (получим величину х - 3);

2) из полученного результата извлечь квадратный корень (получим значение );

3) из этой величины вычесть число 1 (получим значение т. е. значение функции у).

Совокупность этих операций (действий) и есть функция у = f(x) или Очевидно, квадратный корень можно извлечь только из неотрицательной величины. Поэтому х – 3 ≥ 0 и х ≥ 3. Следовательно, область определения функции D(f) = [3; +∞). Квадратный корень (по определению) величина неотрицательная, т. е. . Вычтем из обеих частей этого неравенства число 1 и получим: т. е. у ≥ -1. Поэтому область значений функции E(f) = [-1; +∞).

Пример 2

Найдем область определения функции:

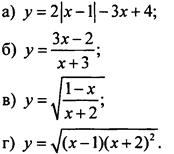
В задаче функция задается некоторой формулой (выражением) и область определения функции совпадает с областью допустимых значений такого выражения.

а) В данное выражение входят операции сложения, вычитания, умножения и нахождения модуля. Все эти операции выполнимы при любых значениях переменной х, т. е. D(f) = (-∞; +∞).

б) В выражение входит деление на величину, зависящую от переменной. Такая операция выполнима, если делитель не равен нулю. Получаем условие: х + 3 ≠ 0, откуда х ≠ -3. Поэтому область определения функции все значения х, за исключением точки (-3), т. е. D(f) = (-∞; - 3)U(-3; +∞) или D(f): х ≠ -3.

в) В выражение входит операция извлечения квадратного корня из алгебраической дроби. Эта операция выполнима, если подкоренное выражение неотрицательно. Получаем неравенство: решение которого -2 < х √ 1. Поэтому область определения функции - промежуток (-2; 1], т. е. D(f) = (-2; 1].

г) Этот пункт аналогичен предыдущему. Область определения функции задается условием (х - 1)(х + 2)² ≥ 0. Решение такого неравенства: отдельная точка х = -2 и промежуток х ∈ [1; +∞). Поэтому область определения функции D(f) = {-2}U[1; +∞).

Заметим, что в этом примере область определения функции явно не указывалась. Такую область находили, учитывая ОДЗ выражения, задающего функцию. Эту область определения иногда называют естественной.

Запись f(а) означает значение функции в точке х = а. Чтобы найти это значение в формуле, задающую функцию, вместо аргумента надо подставить величину а.

Пример 3

Рассмотрим линейную функцию у = 2х + 3. Найдем:

а) Вместо аргумента х подставим число 5 и найдем значение функции

б) Вместо аргумента х подставим величину х - 4 и получим:

в) Аналогично предыдущему пункту вместо аргумента х подставим величину 3х + 1 и найдем значение функции

г) В этом случае рассматривается, т. е. функция, аргументом которой тоже является функция. Получаем:

Подобным образом поступают и в случае кусочной функции.

Пример 4

Рассмотрим функцию у = f(х), где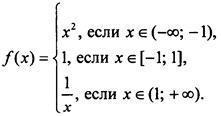

Найдем: f(-3); f(-1); f(0); f(1); f(5).

Область определения функции состоит из трех промежутков: (-∞; -1), [-1; 1] и (1; +∞). Объединив их, получим всю числовую ось, т. е. D(f) = (-∞; +∞). При вычислении значения f(а) надо определить, в какой промежуток попадает точка а. Тогда по соответствующей формуле находим величину f(а).

Точка x = -3 принадлежит первому промежутку. Поэтому используем первую формулу и получаем: f(-3) = (-3)² = 9.

Точки х = -1, x = 0, x = 1 лежат во втором промежутке. Используем вторую строчку формулы, задающей функцию. Находим: f(-1) = f(0) = f(1) = 1.

Точка х = 5 принадлежит третьему промежутку. Используем третью формулу и получаем: f(5) = 1/5 = 0,2.

Часто возникает обратная задача: известно значение функции f(x) в точке а (зависящей от переменной х) и надо найти функцию f(x).

Пример 5

Известно, что Найдем f(х).

Обозначим и выразим из этого равенства переменную х = 6 – 2t. Перепишем условие задачи в виде Получили: f(t) = 4t² – 22t + 30. Так как аргумент функции можно обозначать любой буквой: t, v, х и т. д., то сразу можно записать: f(х) = 4х² - 22х + 30.

Существуют и более сложные задачи, которые решаются подобным образом.

Пример 6

Известно, что

Обозначим t = х - 2 (тогда х = t + 2) и запишем условие задачи: Это равенство запишем также для точки (-t). Получаем: Итак, для нахождения f(t) имеем систему уравнений:

Введем новые переменные: а = f(t) и b = f(-t). Получаем систему линейных уравнений: в которой нас интересует только переменная а. Поэтому используем способ алгебраического сложения. Первое уравнение умножим на число (-2), второе - на число 3. Имеем систему: Сложим уравнения системы: 5а = t² – 35t + 9, откуда или Так же как и в предыдущей задаче, можно написать:

Поведение функции в математике принято изображать специальным рисунком - графиком.

Определение 2. Графиком функции у = f(х), х ∈ X, называют множество F точек (х; у) координатной плоскости хОу: F = {(x; у)|х ∈ Х, y = f(x)}.

По графику функции легко установить область определения и область значений функции у = f(х). Для этого точки графика проецируют на ось абсцисс и ось ординат и находят, соответственно, область определения D(f) и область значений E(f).

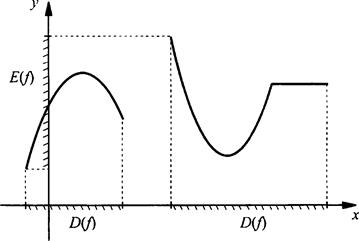
Пример 7

Построим график функции у = f(х), где 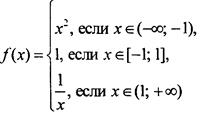(пример 4).

Область определения функции состоит из трех промежутков, на каждом из которых функция задается своей формулой. На луче (-∞; -1) строим график функции y = x² (парабола), на промежутке [-1; 1] - график функции y = 1 (отрезок прямой) и на луче (1; +∞) - график функции y = 1/x (гипербола). Таким образом, получаем график функции f(х):

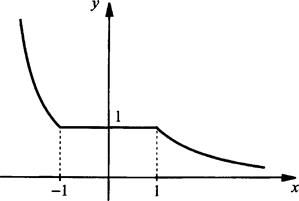
Область определения этой кусочной функции D(f) = (-∞; +∞) и область значений E(f) = (0; +∞).

III. Контрольные вопросы

1. Дайте определение функции и поясните его примером.

2. Область определения и область значений функции.

3. Определение графика функции.

IV. Задание на уроках

§ 8, № 2 (а, б); 3 (в); 4 (а); 7 (в); 9 (а, б); 13 (б, в); 16 (а); 17 (а, б); 20 (в, г); 21 (а); 22; 24 (а, в); 26 (б); 30 (а); 32 (в, г); 33 (а, б); 34; 37; 38.

V. Задание на дом

§ 8, № 2 (в, г); 3 (г); 4 (б); 7 (г); 9 (в, г); 13 (а, г); 16 (г); 17 (в, г); 20 (а, б); 21 (в); 23; 24 (б, г); 26 (в); 30 (г); 32 (а, б); 33 (в, г); 35; 36.

VI. Творческие задания

1. Найдите функцию f(x), если известно:

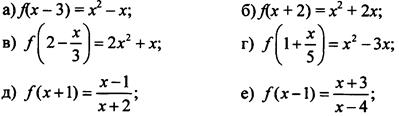
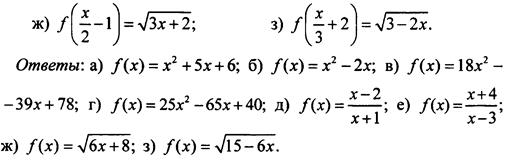
2. Найдите функцию f(х), если известно:

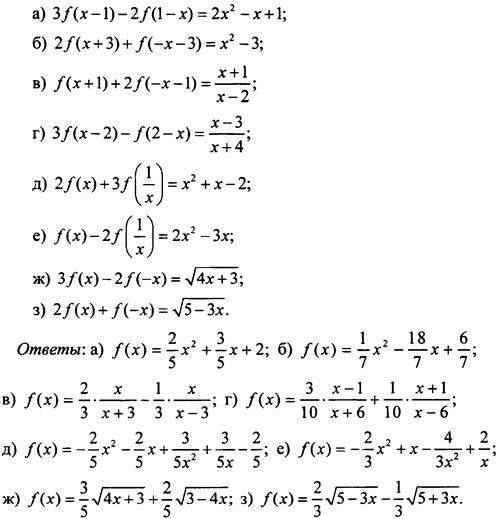
VII. Подведение итогов уроков