Способы задания функции - Числовые функции

Цель: рассмотреть различные способы задания функции и связь между ними.

Ход уроков

I. Сообщение темы и цели уроков

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (самостоятельная работа).

Вариант 1

1. Найдите область определения функции:

2. Постройте график функции у = f{x), где Укажите область определения и область значений функции.

Вариант 2

1. Найдите область определения функции:

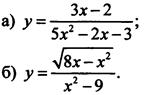
2. Постройте график функции у = f(х), где Укажите область определения и область значений функции.

III. Изучение нового материала

Прежде всего функцию необходимо задать, т. е. указать правило, которое позволяет для каждого значения независимой переменной х из области определения функции найти соответствующее значение зависимой переменной у. В зависимости от формулировки такого правила выделяют три способа задания функции: аналитический, табличный, графический,

а) Аналитический (с помощью формулы или формул)

Пример 1

Рассмотрим функции:

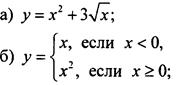
Несмотря на непривычную форму, это соотношение также задает функцию. Для любого значения х легко найти величину у. Например, для х = -0,37 (так как х < 0, то пользуясь верхним выражением) получаем: y(-0,37) = -0,37. Для х = 2/3 (так как х > 0, то пользуемся нижним выражением) имеем Из способа нахождения у понятно, что любой величине х отвечает только одно значение у;

в) 3х + у = 2у - х². Выразим из этого соотношения величину у: 3х + х² = 2у - у или х² + 3х = у. Таким образом, это соотношение также задает функцию у = х² + 3х.

б) Табличный

Пример 2

Выпишем таблицу квадратов у для чисел х.

x	1	1,5	2	2,5	3	4	5	6	7
y	1	2,25	4	6,25	9	16	25	36	49

Такая таблица также задает функцию: для каждого (приведенного в таблице) значения х можно найти единственное значение у. Например, y( 1,5) = 2,25, у(5) = 25 и т. д.

в) Графический

В прямоугольной системе координат для изображения функциональной зависимости у(х) удобно пользоваться специальным рисунком - графиком функции.

Графиком функции у(х) называют множество всех точек системы координат, абсциссы которых равны значениям независимой переменной х, а ординаты - соответствующим значениям зависимой переменной у.

В силу такого определения все пары точек (x₀, у₀), которые удовлетворяют функциональной зависимости y(x), расположены на графике функции. Любые другие пары точек, не удовлетворяющие зависимости у(х), на графике функции не лежат.

Пример 3

Дана функция у = 2х - 3|х| + 4. Принадлежит ли графику этой функции точка с ординатами: а) (-2; -6); б) (-3; -10)?

а) Найдем значение функции у при х =-2: у(-2) = 2 ∙ (-2) - 3|-2| + 4 = -4 - 3 ∙ 2 + 4 = -6. Так как у(-2) = -6, то точка А(-2; -6) принадлежит графику данной функции.

б) Определим значение функции у при x = -3: у(-3) = 2 ∙ (-3) - 3|-3| + 4 = -6 - 3 ∙ 3 + 4 = -11. Так как у(-3) = -11, то точка В(-3; -10) не принадлежит графику этой функции.

Сравним различные способы задания функции. Наиболее полным следует считать аналитический способ. Этот способ позволяет составить таблицу значений функции для некоторых значений аргументов, построить график функции, провести необходимое исследование функции. Вместе с тем, табличный способ позволяет быстро и легко найти значение функции для некоторых значений аргумента. График функции наглядно показывает ее поведение. Поэтому противопоставлять различные способы задания функции не следует: каждый из них имеет свои преимущества и свои недостатки. На практике используются все три способа задания функции.

В дальнейшем будем считать основным аналитический способ задания функции.

Заметим, что не всякое соотношение между переменными x и у является функцией. Функцией называют только такой закон (правило), при котором каждому значению x соответствует только единственное значение у.

Пример 4

Зависимость уже не является функцией. Действительно, если мы хотим вычислить значение у, например, для х = 1, то, пользуясь верхней формулой, найдем у = 2 ∙ 1 - 3 = -1, а пользуясь нижней формулой, получим: у = 1² + 1 = 2. Таким образом, одному значению х (х = 1) соответствуют два значения у (у = -1 и у = 2). Поэтому эта зависимость (по определению) не является функцией.

Пример 5

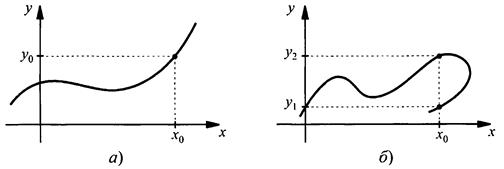
Приведены графики двух зависимостей у(х). Определить, какая из них является функцией.

На рис. а приведен график функции, так как любой точке х₀ соответствует только одно значение у₀. На рис. б приведен график какой-то зависимости (но не функции), так как существуют такие точки (например, х₀), которым отвечает более одного значения у (например, значения у₁ и у₂).

IV. Контрольные вопросы

1. Что означает задать функцию?

2. Основные способы задания функции, их краткая характеристика.

V. Задание на уроках

§ 9, № 1; 3; 6 (а, б); 7; 9 (в, г); 10 (а, б); 13 (в, г); 14; 17 (а); 18 (б); 19 (а).

VI. Задание на дом

§ 9, № 2; 4; 6 (в, г); 8; 9 (а, б); 10 (в, г); 13 (а, б); 15; 17 (б); 18 (a); 19 (б).

VII. Подведение итогов уроков