Поурочные разработки по Алгебре 9 класс к учебнику А. Г. Мордковича - 2011 год
Множества и операции над ними - Рациональные неравенства и их системы
Цель: познакомить с элементами теории множеств.
Ход уроков
I. Сообщение темы и цели уроков
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (самостоятельная работа).
Вариант 1
1. Методом интервалов решите неравенство:
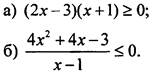
2. Найдите область определения функции ![]()
Вариант 2
1. Методом интервалов решите неравенство:
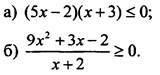
2. Найдите область определения функции ![]()
III. Изучение нового материала
Этот урок имеет вспомогательный характер: из теории множеств нужны простейшие понятия, необходимые для грамотной записи ответов в алгебраических задачах. Поэтому изложим материал урока предельно кратко и в минимально необходимом объеме для дальнейшего изучения курса 9 класса.
1. Понятие множества
Множеством называют совокупность элементов, отобранных по определенному признаку (признакам). Множество может содержать конечное или бесконечное количество элементов, а также вообще не иметь элементов (во многих случаях заранее неизвестно, будут ли в рассматриваемом множестве элементы).
Пример 1
а) Множество А простых делителей числа 30 состоит из трех элементов: 2; 3; 5.
б) Множество В натуральных четных чисел содержит бесконечное количество элементов: 2; 4; 6; ... .
в) Множество С корней уравнения |х| + 3х2 + 5 = 0 не содержит ни одного элемента.
Если множество содержит небольшое число элементов, то обычно такое множество задают перечислением его элементов.
В примере 1а множество А = {2; 3; 5}. В случае бесконечного количества элементов множество также можно задавать перечислением нескольких первых элементов, так чтобы было понято правило отбора элементов множества. В примере 16 множество В = {2; 4; 6; ...}. Для наиболее часто встречающихся в математике числовых множеств есть специальные обозначения:
R - множество действительных чисел,
Q - множество рациональных чисел,
Z - множество целых чисел,
N - множество натуральных чисел.
Для обозначения пустого множества (т. е. множества, не содержащего элементов) вводится специальный символ Ø.
Вообще говоря, способы задания множеств могут быть самыми разнообразными.
Пример 2
а) Множество (х|3 ≤ x < √17} - множество всех чисел, которые не меньше 3 и меньше √17, т. е. промежуток [3; √17) или {х|3 ≤ x < √17} = [3; √17).
б) Множество {x|x2 - 4 < 0} - множество решений неравенства х2 - 4 < 0, т. е. промежуток (-2; 2) или {х|x2 - 4 < 0} = (-2; 2).
в) Множество {х|(3х - 2)(x + 1) = 0} - множество решений уравнения (3х - 2)(х + 1) = 0, т. е. числа х1 = 2/3 и х2 = -1 или ![]()
Во многих случаях необходимо выяснить, является ли а элементом множества А (или принадлежит ли элемент а множеству А), и записать результат. Для подобных случаев существуют специальные обозначения:
а ∈ А - элемент а принадлежит множеству А,
a ∉ А - элемент а не принадлежит множеству А.
Пример 3
Пусть множество А = {2; √5; 4}. Тогда √5 ∈ А, а 3 ∉ А.
Для иллюстрации в теории множеств пользуются диаграммами Эйлера. Рассматривают в качестве множества А множество точек плоской фигуры. Тогда понятия принадлежности и непринадлежности элемента а множеству А можно изобразить наглядно.
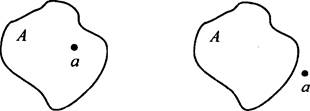
2. Подмножество
Во многих случаях рассматривают не все элементы множества А, а только часть этих элементов. Тогда говорят, что эта часть элементов является подмножеством В множества А. Дадим более строгое определение подмножества.
Определение 1. Если каждый элемент множества В является элементом множества А, то множество В называют подмножеством множества A.
Такую ситуацию обозначают символом ⊂ (знак ⊂ - знак включения), т. е. В ⊂ А. Наглядно подмножество можно иллюстрировать диаграммой Эйлера.
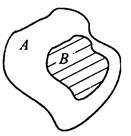
Пример 4
Рассмотрим множество А = {1; 2; 3}, состоящее из грех элементов. Какие подмножества есть у этого трехэлементного множества? Перечислим их.
Одноэлементные подмножества: {1}, {2}, {3}.
Двухэлементные подмножества: {1,2}, {2; 3}, {1; 3}.
Трехэлементное подмножество - само множество А = {1; 2; 3}.
Подмножество без элементов - пустое множество Ø.
Всего можно получить 23 = 8 подмножеств. Вообще говоря, множество, состоящее из n элементов, содержит 2n подмножеств.
Пример 5
Разберемся с основными числовыми множествами. Очевидно, множество натуральных чисел N - часть множества целых чисел Z, которое, в свою очередь, - часть множества рациональных чисел Q. Последнее множество Q - часть множества действительных чисел R.
Весь этот абзац математически записывается кратко и четко: N ⊂ Z ⊂ Q ⊂ R.
3. Пересечение и объединение множеств
Рассмотрим две основные операции над множествами: пересечение и объединение множеств.
Определение 2. Пересечением множеств А и В называют множество С, состоящее из всех общих элементов множеств A и В. Это множество обозначают так: С = A ∩ В = {х|х ∈ А и х ∈ В}.
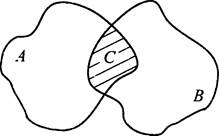
Пример 6
Пусть А = {1; 5; 7; 2; 3} и B = {3; 5; 4; 8; 1}.
Найдем пересечение этих множеств С = А ∩ В = {1; 3; 5}.
Пример 7
Пусть множество А = [2; 7] и множество В = (3; 9).
Очевидно, пересечением этих промежутков является множество С = A ∩ B = (3; 7].
Пример 8
После страшной битвы вся команда пиратского корабля получила ранения: ранены в руку - 40 человек, в ногу - 80 пиратов, невезучие (ранены и в руку, и в ногу) - 30 человек. Сколько пиратов в команде корабля?
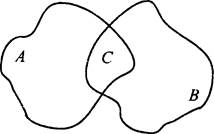
Пусть А - множество человек, раненных в руку (40 чел.), В - множество пиратов, раненных в ногу (80 чел.), и С = A ∩ В - множество человек, получивших два ранения (30 чел.). Найдем число пиратов, раненных только в руку: 40 - 30 = 10 - и только в ногу: 80 - 30 = 50. Так как каждый пират имеет хотя бы одно ранение, то всего пиратов: 10 + 50 + 30 = 90 человек.
Определение 3. Объединением множества А и В называют множество С, состоящее из элементов, входящих хотя бы в одно из множеств А или В. Это множество обозначают так: С = A U В = {x|x∈ А или х ∈ В).
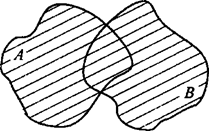
Пример 9 (сравните с примером 6)
Пусть А = {1; 5; 7; 2; 3} и В = {3; 5; 4; 8; 1}. Найдем объединение этих множеств С = A U В = {1; 2; 3; 4; 5; 7; 8}.
Пример 10 (сравните с примером 7)
Пусть множество А = [2; 7] и множество В = (3; 9). Очевидно, объединением этих промежутков является множество С = A U B = [2; 9).
IV. Контрольные вопросы
1. Что называют множеством?
2. Как обозначаются основные числовые множества?
3. Определение подмножества В множества А.
4. Операция пересечение множеств.
5. Объединение множеств.
V. Задание на уроках
§ 3, № 1 (а, в); 3 (а, г); 7; 10; 12 (а, в); 13; 15 (а, г); 20 (б); 23.
VI. Задание на дом
§ 3, № 1 (б, г); 3 (б, в); 8; 11; 12 (б, г); 14; 15 (б, в); 20 (в); 24.
VII. Подведение итогов уроков