Системы неравенств - Рациональные неравенства и их системы

Цель: рассмотреть решение системы неравенств с одной переменной.

Ход уроков

I. Сообщение темы и цели уроков

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (письменный опрос).

Вариант 1

1. Пересечение множеств А и В.

2. Даны множества А = {3; 1; 4; 2; 7} и В = {1; 8; 6; 3; 2}. Найдите пересечение и объединение этих множеств.

3. Даны множества А = [-3; 5) и В = (-1; 8). Найдите пересечение и объединение этих промежутков.

Вариант 2

1. Объединение множеств А и В.

2. Даны множества А = {2; 5; 1; 8; 3 } и В = {9; 4; 3; 5; 2}. Найдите пересечение и объединение этих множеств.

3. Даны множества А = [-4; 7) и В = [-2; 10). Найдите пересечение и объединение этих промежутков.

III. Изучение нового материала

Часто возникает задача нахождения общих решений нескольких неравенств с одной переменной. Тогда возникает понятие системы неравенств.

Определение. Несколько неравенств с одной переменной х образуют систему неравенств, если необходимо найти все значения переменной, при которых каждое неравенство обращается в верное числовое неравенство (т. е. найти общие решения данных неравенств). Любое такое значение переменной х называют решением (или частным решением) системы неравенств. Множество всех частных решений системы неравенств является общим решением системы неравенств (или, проще, решением системы неравенств).

Неравенства, образующие систему, объединяются фигурной скобкой (как и в системах уравнений) или записываются в виде двойного неравенства.

Пример 1

а) Запись означает, что неравенства 3х - 2 ≥ 1 и 2х - 1 < 3 образуют систему и необходимо искать общие решениях этих неравенств.

б) Запись 2х - 1 < 3х + 2 ≤ 4х + 3 эквивалентна записи Тогда неравенства 2х - 1 < 3х + 2 и 3х + 2 ≤ 4х + 3 образуют систему и необходимо искать общие решения этих неравенств.

Решить систему неравенств - значит найти все ее решения или доказать, что решений нет. Поэтому для решения системы неравенств пользуются определением: решают каждое неравенство системы отдельно, потом находят общее решение из ранее полученных.

Пример 2

Решим системы неравенств из примера 1.

а) Для системы линейных неравенств решение первого неравенства х ≥ 1, второго неравенства - х < 2. Отметим эти решения на одной координатной прямой штриховкой: для первого неравенства - сверху, для второго неравенства - снизу.

Видно, что общими решениями (т. е. решением системы неравенств) является промежуток [1; 2). Этот промежуток будет Пересечением множеств решений каждого неравенства: х₁ = [1; +∞) и х₂ = (-∞; 2) - область двойной штриховки.

б) Для системы линейных неравенств решение первого неравенства х > -3, второго неравенства - х ≥ -1. Отметим эти решения на одной координатной прямой штриховкой: для первого неравенства - сверху, для второго неравенства - снизу.

Видно, что общими решениями (т. е. решением системы неравенств или двойного неравенства) является промежуток [-1; +∞). Этот промежуток будет пересечением множеств решений каждого неравенства: х₁ = (-3; +∞) и х₂ = [-1; +∞) - область двойной штриховки.

Учитывая пример 2, можем сформулировать алгоритм решения системы неравенств

1) находят множество х₁ решений неравенства f(x) v 0 и множества х₂ решений неравенства g(x) v 0;

2) находят пересечение х₁∩ х₂ этих множеств, которое и является решением данной системы неравенств.

При решении систем неравенств полезно учитывать два очевидных соображения:

1) если в системе из нескольких неравенств одно неравенство не имеет решений, то и вся система не имеет решений;

2) если в системе из нескольких неравенств одно неравенство выполняется при всех значениях переменной, то решением является решение системы, образованной остальными неравенствами.

Пример 3

а) Решим систему неравенств

Запишем систему в виде или Очевидно, что первое неравенство системы не имеет решений. Тогда и вся система неравенств не имеет решений, т. е. х ∈ Ø.

б) Решим систему неравенств

Запишем систему в виде Решением первого неравенства является любое действительное число х, т. е. х ∈ R. Поэтому достаточно решить второе неравенство 5х - 8 ≥ 0. Его решение х ∈ [1,6; +∞) является также решением всей системы неравенств.

По изложенному алгоритму решаются и более сложные системы неравенств.

Пример 4

Решим систему неравенств

Для решения используем аналитический (метод интервалов) и графический способы.

а) Решим сначала первое неравенство х² + 4х + 3 ≤ 0. Найдем корни соответствующего уравнения х² + 4х + 3 = 0: х₁ = - 3 и х₂ = -1. Нанесем эти точки на числовую ось, которые разбивают ее на три интервала. Определим знак выражения х² + 4х + 3, например, при х = 0: 0² + 4 ∙ 0 + 3 = 3 > 0. После этого легко нарисовать диаграмму знаков рассматриваемого выражения.

Видно, что неравенство выполняется при х ∈ [-3; -1].

Теперь рассмотрим второе неравенство х² + 3х + 2 ≥ 0. Корни этого выражения х₁ = -2 и х₂ = -1. Наносим эти точки на числовую ось. Определяем знак выражения х² + 3х + 2, например, при х = 5 : 5² + 3 ∙ 5 + 2 = 42 > 0. Рисуем диаграмму знаков для этого выражения.

Видно, что неравенство выполняется для х ∈ (-∞; -2]U[-1; +∞).

Найдем те значения х, при которых выполнены оба неравенства. Для этого еще раз нанесем решения первого (штриховка сверху) и второго (штриховка снизу) неравенств на числовую ось. Видно, что оба неравенства выполнены для промежутка х ∈ [-3; -2] и в отдельной точке х = -1.

Итак, решение данной системы неравенств х ∈ [-3; -2]U{-1}.

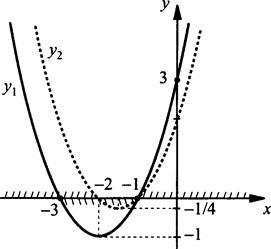
б) Построим графики функций у₁ = х² + 4х + 3 и у₂ = х² + 3х + 2. Видно, что неравенство х² + 4х + 3 ≤ 0 (график у₁ находится не выше оси абсцисс) выполнено для х ∈ [-3; -1]. Неравенство х² + 3х + 2 ≥ 0 (график у₂ находится не ниже оси абсцисс) выполнено при х ∈ [-∞; -2]U[-1; +∞). Оба неравенства выполнены для х ∈ [-3; -2)U{-1}.

При решении систем неравенств целесообразно начинать решение с самого простого неравенства.

Пример 5

Решим систему неравенств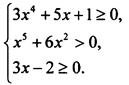

Решение системы начнем с третьего неравенства. Его решение: х ≥ 2/3 (тогда х > 0). Очевидно, что при положительных значениях х каждое слагаемое в левых частях первого и второго неравенств положительно. Поэтому первое и второе неравенства выполнены. Следовательно, решение третьего неравенства х ∈ [2/3; +∞) является также решением всей системы неравенств.

IV. Контрольные вопросы

1. Определение системы неравенств.

2. Частное и общее решения системы неравенств.

3. Алгоритм решения системы неравенств.

V. Задание на уроках

§ 4, № 1 (а, б); 2 (а); 6 (а, г); 9 (а, б); 12 (г); 14 (а, б); 17 (в, г); 18; 23 (а); 26 (г); 29 (б); 31 (а); 35 (а, б); 36 (в, г); 38 (а, б); 39 (а).

VI. Задание на дом

§ 4, № 1 (в, г); 2 (б); 6 (б, в); 9 (в, г); 12 (б); 14 (в, г); 17 (а, б); 19; 23 (б); 26 (а); 29 (г); 31 (б); 35 (в, г); 36 (а, б); 38 (в, г); 39 (б).

VII. Подведение итогов уроков