Зачетная работа по теме «Тригонометрические функции» - Тригонометрические функции - 1-е полугодие

Цель: проверить знания учащихся по вариантам одинаковой сложности.

Ход уроков

I. Сообщение темы и цели уроков

II. Характеристика зачетной работы

III. Варианты зачетной работ.

Вариант 1

А

1. Найдите значение выражения

2. Упростите выражение

3. Найдите наименьшее и наибольшее значения функции и ее область определения.

4. Решите неравенство

5. Известно, что Найдите остальные тригонометрические функции а.

6. Постройте график:

а) функции у = sin 2х +1;

б) уравнения cos(x + у) = 0.

В

7. Упростите выражение

8. Известно, что Найдите значение выражения sin t - cos t.

9. Решите неравенство

10. Постройте график функции

С

11. Найдите наименьшее и наибольшее значения функции

12. Известно, что sin t + cos t = a. Найдите

13. Постройте график функции

Вариант .

А

1. Найдите значение выражения

2. Упростите выражение

3. Найдите наименьшее и наибольшее значения функции у = 5 - 2 sin2 2х и ее область определения.

4. Решите неравенство

5. Известно, что Найдите остальные тригонометрические функции а.

6. Постройте график:

а) функции у = cos 2х -1;

б) уравнения sin(y - х) = 0.

В

7. У простите выражение

8. Известно, что Найдите значение выражения sin t + cos t.

9. Решите неравенство

10. Постройте график функции

С

11. Найдите наименьшее и наибольшее значения функции

12. Известно, что sin t + cos t = а. Найдите

13. Постройте график функции

IV. Ответы и решени.

Вариант 1

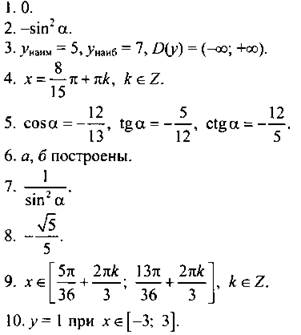
11. Используя основное тригонометрическое тождество, запишем функцию в виде Введем новую переменную z = sin x и -1 ≤ z ≤ 1. Тогда функция имеет вид: На отрезке z ∈ [-1; 1] наименьшее значение функции достигается при z = 1/4, и оно равно 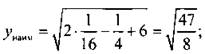наибольшее значение достигается при z = -1, и оно равно

Ответ:

12. Возведем равенство sin t + cos t = a в квадрат и получим: откуда Используем формулу суммы кубов

Ответ:

13. Данную функцию запишем в виде 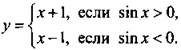Выделим промежутки, на которых sin x > 0, и построим график функции у = х + 1. На промежутках, на которых sin х < 0, строим график функции у = х - 1.

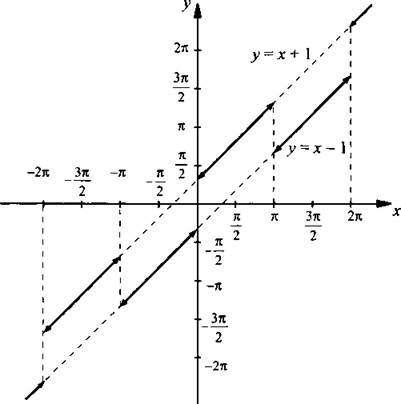
Ответ: график построен.

Вариант 2

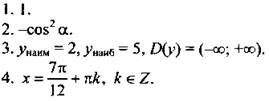
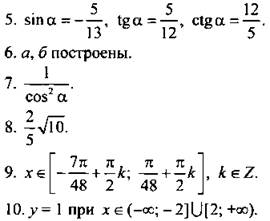
11. Используя основное тригонометрическое тождество, запишем функцию в виде Введем новую переменную z = sin х, -1 ≤ z ≤ 1. Тогда функция имеет вид: На отрезке z ∈ [-1; 1] наименьшее значение функции достигается при z = -1/2, и оно равно 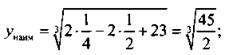наибольшее значение достигается при z = 1, и оно равно

Ответ: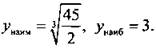

12. Возведем равенство sin t + cos t = а в квадрат и получим: откуда Используем формулу квадрата суммы:

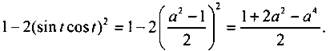
Ответ: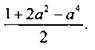

13. Данную функцию запишем в виде 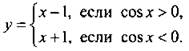Выделим промежутки, на которых cos х > 0, и построим график функции у = х - 1. На промежутках, на которых cos х < 0, строим график функции у = х + 1.

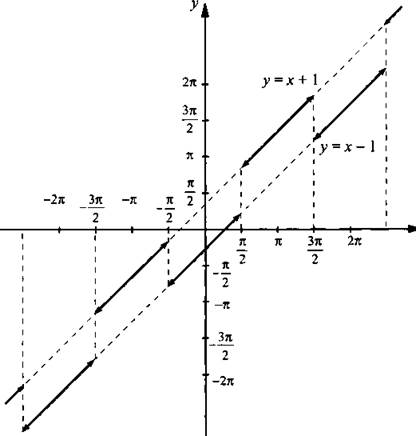
Ответ: график построен.