Алгебра и начала анализа 10 класс поурочные планы по учебнику Мордковича А. Г.
Обратные тригонометрические функции - Тригонометрические уравнения - 1-е полугодие
В предыдущей главе уже рассматривалось решение самых простых тригонометрических уравнении, например ![]()
![]() и т. д.
и т. д.
Теперь изложенные подходы надо обобщить и применить для решения уравнений вида sin х = a, cos х = a, tg х = a, ctg х = а и более сложных. Для этого надо изучить обратные тригонометрические функции - арксинус, арккосинус, арктангенс и арккотангенс.
Уроки 32-33. Обратные тригонометрические функции
Цель: рассмотреть обратные тригонометрические функции, их использование для записи решений тригонометрических уравнений.
Ход уроков
I. Сообщение темы и цели уроков
II. Изучение нового материала
1. Обратные тригонометрические функции
Рассмотрение этой темы начнем со следующего примера.
Пример 1
Решим уравнение: a) sin x = 1/2; б) sin x = а.
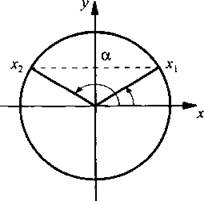
а) На оси ординат отложим значение 1/2 и построим углы x1 и х2, для которых sin x = 1/2. При этом х1 + х2 = π, откуда х2 = π – x1. По таблице значений тригонометрических функций найдем величину х1 = π/6, тогда ![]() Учтем периодичность функции синуса и запишем решения данного уравнения:
Учтем периодичность функции синуса и запишем решения данного уравнения: ![]() где k ∈ Z.
где k ∈ Z.
б) Очевидно, что алгоритм решения уравнения sin х = а такой же, как и в предыдущем пункте. Разумеется, теперь по оси ординат откладывается величина а. Возникает необходимость каким-то образом обозначить угол х1. Условились такой угол обозначать символом arcsin а. Тогда решения данного уравнения можно записать в виде ![]() Эти две формулы можно объединить в одну:
Эти две формулы можно объединить в одну: ![]() при этом
при этом ![]()
Аналогичным образом вводятся и остальные обратные тригонометрические функции.
Очень часто бывает необходимо определить величину угла по известному значению его тригонометрической функции. Такая задача является многозначной - существует бесчисленное множество углов, тригонометрические функции которых равны одному и тому же значению. Поэтому, исходя из монотонности тригонометрических функций, для однозначного определения углов вводят следующие обратные тригонометрические функции.
Арксинус числа a (arcsin а) - такой угол а из промежутка ![]() , синус которого равен а, т. е.
, синус которого равен а, т. е. ![]()
Арккосинус числа a (arccos а) - такой угол а из промежутка [0; π], косинус которого равен а, т. е. ![]()
Арктангенс числа a (arctg а) - такой угол а из промежутка ![]() тангенс которого равен а, т. е.
тангенс которого равен а, т. е. ![]() tg а = а.
tg а = а.
Арккотангенс числа a (arcctg а) - такой угол а из промежутка (0; π), котангенс которого равен а, т. е. ![]() ctg а = а.
ctg а = а.
Пример 2
Найдем:
![]()
Учитывая определения обратных тригонометрических функций получим:
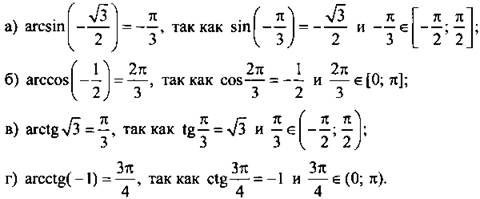
Пример 3
Вычислим ![]()
Пусть угол а = arcsin 3/5, тогда по определению sin a = 3/5 и 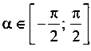 . Следовательно, надо найти cos а. Используя основное тригонометрическое тождество, получим:
. Следовательно, надо найти cos а. Используя основное тригонометрическое тождество, получим: 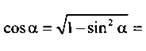
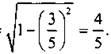 Учтено, что
Учтено, что 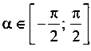 и cos a ≥ 0. Итак,
и cos a ≥ 0. Итак, ![]()
Рассмотрим более подробно свойства обратных тригонометрических функций.
Свойства функции |
Функция |
|||
у = arcsin х |
у = arccos х |
у = arctg х |
у = arcctg х |
|
Область определения |
х ∈ [-1; 1] |
х ∈ [-1; 1] |
х ∈ (-∞; +∞) |
х ∈ (-∞ +∞) |
Область значений |
y ∈ [-π/2; π/2] |
y ∈ [0; π] |
y ∈ (-π/2; π/2) |
y ∈ (0; π) |
Четность |
Нечетная |
Ни четная, ни нечетная |
Нечетная |
Ни четная, ни нечетная |
Нули функции (y = 0) |
При х = 0 |
При х = 1 |
При х = 0 |
у ≠ 0 |
Промежутки знакопостоянства |
у > 0 при х ∈ (0; 1]. у < 0 при х ∈ [-1; 0) |
у > 0 при х ∈ [-1; 1) |
у > 0 при х ∈ (0; +∞). у < 0 при х ∈ (-∞; 0) |
у > 0 при x ∈ (-∞; +∞) |
Монотонность |
Возрастает |
Убывает |
Возрастает |
Убывает |
Связь с тригонометрической функцией |
sin у = х |
cos у = х |
tg у = х |
ctg у = х |
График |
а |
б |
в |
г |
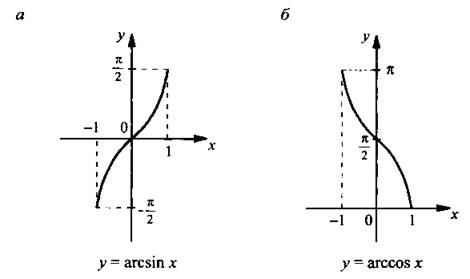
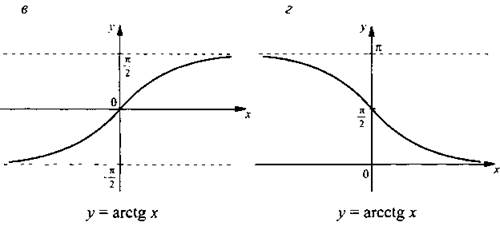
Приведем еще ряд типичных примеров, связанных с определениями и основными свойствами обратных тригонометрических функций.
Пример 4
Найдем область определения функции ![]()
Для того чтобы функция у была определена, необходимо выполнение неравенства ![]() которое эквивалентно системе неравенств
которое эквивалентно системе неравенств 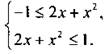 Решением первого неравенства является промежуток х ∈ (-∞; +∞), второго -
Решением первого неравенства является промежуток х ∈ (-∞; +∞), второго - ![]() Этот промежуток
Этот промежуток ![]() и является решением системы неравенств, а следовательно, и областью определения функции
и является решением системы неравенств, а следовательно, и областью определения функции ![]()
Пример 5
Найдем область изменения функции ![]()
Рассмотрим поведение функции z = 2х - х2 (см. рисунок).
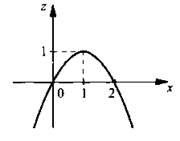
Видно, что z ∈ (-∞; 1]. Учитывая, что аргумент z функции арккотангенса меняется в указанных пределах, из данных таблицы получим, что ![]() Таким образом, область изменения
Таким образом, область изменения ![]()
Пример 6
Докажем, что функция у = arctg х нечетная. Пусть ![]() Тогда tg а = -х или х = -tg а = tg(-a), причем
Тогда tg а = -х или х = -tg а = tg(-a), причем ![]() Следовательно, - a = arctg х или а = -arctg х. Таким образом, видим, что
Следовательно, - a = arctg х или а = -arctg х. Таким образом, видим, что ![]() т. е. у(х) - функция нечетная.
т. е. у(х) - функция нечетная.
Пример 7
Выразим через все обратные тригонометрические функции ![]()
Пусть ![]() Очевидно, что
Очевидно, что 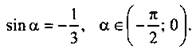 Тогда
Тогда 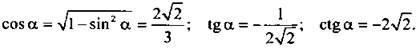 Так как
Так как 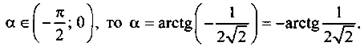
Введем угол ![]() Так как
Так как 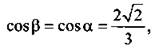 то
то ![]()
Аналогично ![]() поэтому
поэтому ![]() и
и ![]()
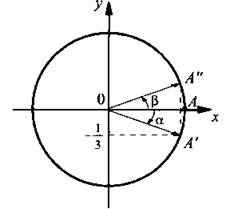
Итак, 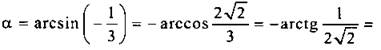
![]()
Пример 8
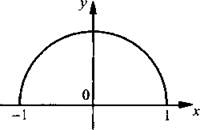
Построим график функции у = cos(arcsin х).
Обозначим а = arcsin x, тогда 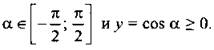 Учтем, что х = sin а и у = cos а, т. е. x2 + у2 = 1, и ограничения на х (х ∈ [-1; 1]) и у (у ≥ 0). Тогда графиком функции у = cos(arcsin х) является полуокружность.
Учтем, что х = sin а и у = cos а, т. е. x2 + у2 = 1, и ограничения на х (х ∈ [-1; 1]) и у (у ≥ 0). Тогда графиком функции у = cos(arcsin х) является полуокружность.
Пример 9
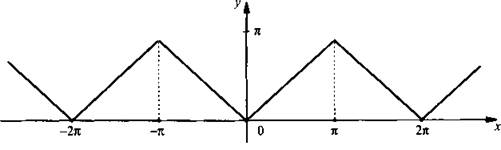
Построим график функции у = arccos(cos x).
Так как функция cos х изменяется на отрезке [-1; 1], то функция у определена на всей числовой оси и изменяется на отрезке [0; π]. Будем иметь в виду, что у = arccos(cos x) = х на отрезке [0; π]; функция у является четной и периодической с периодом 2π. Учитывая, что этими свойствами обладает функция cos x, теперь легко построить график.
Отметим некоторые полезные равенства:
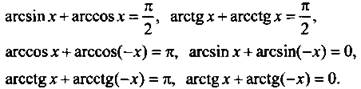
Пример 10
Найдем наименьшее и наибольшее значения функции ![]() Обозначим
Обозначим ![]() тогда
тогда ![]() Получим функцию
Получим функцию 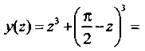
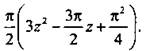 Эта функция имеет минимум в точке z = π/4, и он равен
Эта функция имеет минимум в точке z = π/4, и он равен 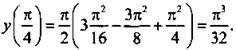 Наибольшее значение функции достигается в точке z = -π/2, и оно равно
Наибольшее значение функции достигается в точке z = -π/2, и оно равно 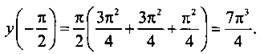 Таким образом,
Таким образом, 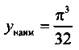 и
и ![]()
Пример 11
Решим уравнение ![]()
Учтем, что ![]() Тогда уравнение имеет вид:
Тогда уравнение имеет вид: ![]() или
или ![]() откуда
откуда ![]() По определению арктангенса получим:
По определению арктангенса получим: ![]()
2. Решение простейших тригонометрических уравнений
Аналогично примеру 1 можно получить решения простейших тригонометрических уравнений.
Уравнение |
Решение |
|
|
|
|
tgx = а |
|
ctg х = а |
|
Пример 12
Решим уравнение ![]()
Так как функция синус нечетная, то запишем уравнение в виде 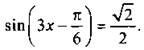 Решения этого уравнения:
Решения этого уравнения: ![]()
![]() откуда находим
откуда находим ![]()
![]()
Пример 13
Решим уравнение ![]()
По приведенной формуле запишем решения уравнения: ![]() и найдем
и найдем ![]()
Заметим, что в частных случаях (а = 0; ±1) при решении уравнений sin х = а и cos х = а проще и удобнее использовать не общие формулы, а записывать решения на основании единичной окружности:
для уравнения sin х = 1 решения ![]()
для уравнения sin х = 0 решения х = πk;
для уравнения sin х = -1 решения ![]()
для уравнения cos х = 1 решения х = 2πk.
для уравнения cos х = 0 решения ![]()
для уравнения cos х = -1 решения ![]()
Пример 14
Решим уравнение ![]()
Так как в данном примере имеется частный случай уравнения, то по соответствующей формуле запишем решение: ![]() откуда найдем
откуда найдем ![]()
III. Контрольные вопросы (фронтальный опрос)
1. Дайте определение и перечислите основные свойства обратных тригонометрических функций.
2. Приведите графики обратных тригонометрических функций.
3. Решение простейших тригонометрических уравнений.
IV. Задание на уроках
§ 15, № 3 (а, б); 4 (в, г); 7 (а); 8 (а); 12 (б); 13 (а); 15 (в); 16 (а); 18 (а, б); 19 (в); 21;
§ 16, № 4 (а, б); 7 (а); 8 (б); 16 (а, б); 18 (а); 19 (в, г);
§ 17, № 3 (а, б); 4 (в, г); 5 (а, б); 7 (в, г); 9 (б); 10 (а, в).
V. Задание на дом
§ 15, № 3 (в, г); 4 (а, б); 7 (в); 8 (б); 12 (а); 13 (б); 15 (г); 16 (б); 18 (в, г); 19 (г); 22;
§ 16, № 4 (в, г); 7 (б); 8 (а); 16 (в, г); 18 (б); 19 (а, б);
§ 17, № 3 (в, г); 4 (а, б); 5 (в, г); 7 (а, б); 9 (г); 10 (б, г).
VI. Творческие задания
1. Найдите область определения функции:
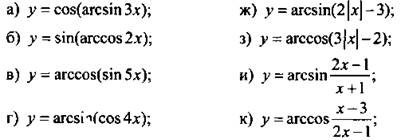

Ответы: ![]()
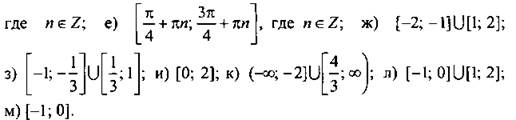
2. Найдите область значений функции:
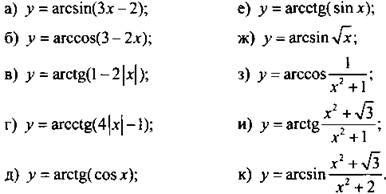
Ответы: ![]()
![]()
3. Постройте график функции:
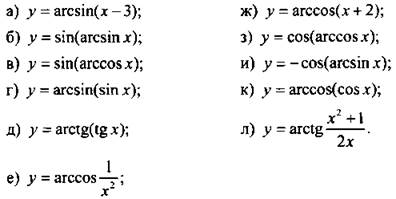
VII. Подведение итогов уроков