Алгебра и начала анализа 10 класс поурочные планы по учебнику Мордковича А. Г.
Определение производной - Производная - 2-е полугодие
Цель: рассмотреть понятия производной, мгновенной скорости движения тела, касательной к графику функции.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (письменный опрос).
Вариант 1
1. Дайте определение средней скорости движения тела.
2. Выразите приращение функции f(х) в точке х0 через х0 и Δх, если:
![]()
3. Вычислите:
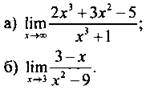
Вариант 2
1. Дайте определение средней скорости изменения функции.
2. Выразите приращение функции f(х) в точке х0 через х0 и Δх, если:
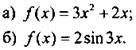
3. Вычислите:
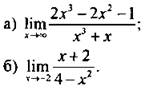
III. Изучение нового материала
Производная является одним из важнейших понятий математического анализа и позволяет проводить исследование функций и строить их графики.
1. Задачи, приводящие к понятию производно.
Задача 1. Мгновенная скорость движения
Рассмотрим физическую задачу на определение мгновенной скорости движения. Пусть точка движется по прямой и ее координата x в момент времени t равна S(t). Предполагаем, что движение происходит непрерывно и плавно (как в реальной жизни). Возникает задача: по известной зависимости S(t) определить скорость V(t), с которой движется точка в момент времени t (такая скорость называется мгновенной).
Если зависимость S(t) линейная, то задача имеет простое решение: в любой момент времени скорость есть отношение пройденного пути ко времени. Если движение неравномерное, то решение задачи усложняется. Сначала найдем среднюю скорость за промежуток времени Δt от t0 до t0 + Δt. Эта скорость Vср(Δt) равна ΔS/Δt. Очевидно, если Δt очень мало, то за такой промежуток времени скорость практически не меняется. Поэтому средняя скорость Vср(Δt) почти не отличается от мгновенной скорости Vмгн(t0). Тогда возникает следующий способ вычисления мгновенной скорости - надо найти Vср(Δt) и определить, к какому значению она стремится, если Δt практически равно нулю, т. е. ![]()
Пример 1
Найдем мгновенную скорость тела при равноускоренном (равнозамедленном) движении.
При таком движении координата тела меняется по закону ![]() где S0 и V0- начальные координата и скорость; а - ускорение тела.
где S0 и V0- начальные координата и скорость; а - ускорение тела.
1) Найдем приращение координаты ![]()
![]()
2) Определим среднюю скорость: ![]()
3) Вычислим мгновенную скорость. Для этого будем уменьшать Δt, приближая эту величину к нулю (для краткости говорят, что Δt стремится к нулю, и записывают: Δt → 0). Тогда выражение ![]() при Δt → 0, величины V0 и аt0 постоянны. Получим, что при Δt → 0 величина
при Δt → 0, величины V0 и аt0 постоянны. Получим, что при Δt → 0 величина ![]() Итак, мгновенная скорость
Итак, мгновенная скорость ![]()
Задача 2. Касательная к графику функции
Практически все рассматриваемые в школе функции имеют графики, представляющие собой гладкие кривые. Рассмотрим поведение таких кривых. Для этого еще раз вернемся к рисунку предыдущего урока.
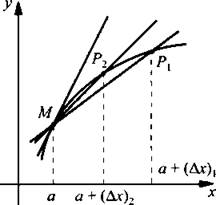
Рассмотрим график функции у = f(x) и точки ![]()
![]() принадлежащие графику. Через точки М и Р1, М и Р2 проведем секущие МР1 и МР2.
принадлежащие графику. Через точки М и Р1, М и Р2 проведем секущие МР1 и МР2.
При небольших значениях Δх секущие МР1 и МР2 мало отличаются от соответствующих дуг. Видно, что с уменьшением Δх различие между секущей и дугой уменьшается. Очевидно, что при стремлении положения точек Р1 и Р2 к положению точки М секущие МР1 и МР2 становятся касательными. Таким образом, при х, близких к а, график функции f(x) практически совпадает с графиком касательной, проведенной в точке а. Поэтому необходимо знать поведение такой касательной, т. е. уравнение касательной. Координаты одной точки касательной известны - это точка (a; f(a)). Остается определить угловой коэффициент k касательной, т. е. к = ![]()
Пример 2
Получим уравнение касательной, проведенной к графику функции f(x) = х3 в точке а = 1.
Угловой коэффициент k(Δх) секущей, проходящей через точки (a; f(а)) и (а + Δх; f(а + Δх)), равен Δf/Δx, где Δf- приращение функции f(х) в точке а, соответствующее приращению Δх аргумента. Для функции f(х) = х3 получим: ![]()
![]() Теперь найдем угловой коэффициент k касательной. Коэффициент k(Δх) будет стремиться к величине k, если Δх приближается к нулю, т. е.
Теперь найдем угловой коэффициент k касательной. Коэффициент k(Δх) будет стремиться к величине k, если Δх приближается к нулю, т. е. ![]() При а = 1 находим: k = 3 и f(a) = 13 = 1.
При а = 1 находим: k = 3 и f(a) = 13 = 1.
Уравнение касательной имеет вид: у = kх + b или у = 3х + b. Так как эта касательная проходит через точку (1; 1), то получаем условие 1 = 3 · 1 + b, откуда b = -2. Итак, уравнение касательной имеет вид: у = 3х -2. Следовательно, при х, близких к а = 1, функция f(х) = a3 ведет себя примерно как касательная у = 3х - 2.
Таким образом, две совершенно различные задачи привели к одной и той же математической модели - пределу отношения приращения функции Δf к приращению аргумента Δх при условии, что приращение аргумента Δх стремится к нулю, т. е. ![]() Многие задачи науки и техники приводят к такой же модели. Поэтому эту математическую модель необходимо изучить, т. е.:
Многие задачи науки и техники приводят к такой же модели. Поэтому эту математическую модель необходимо изучить, т. е.:
а) присвоить ей термин и дать ее формальное определение;
б) ввести для нее обозначение;
в) исследовать свойства новой модели;
г) определить ее область применения.
2. Определение производной
Два рассмотренных примера о нахождении уравнения касательной к данной кривой и вычислении мгновенной скорости тела имели различные формулировки, но решались фактически с использованием одинакового алгоритма. Применительно к произвольной функции f(х) и любой точке х0 ее области определения такой алгоритм (схема) имеет вид.
1) С помощью формулы, задающей функцию f(х), найдем ее приращение в точке х0 и получаем: ![]()
2) Определяем выражение для разностного отношения ![]() которое затем преобразуем (упрощаем, сокращаем на Δх и т. д.).
которое затем преобразуем (упрощаем, сокращаем на Δх и т. д.).
3) Вычисляем, к какому числу стремится отношение Δf/Δx, если Δх стремится к нулю, т. е. находим ![]()
Найденное подобным образом число называют производной функции f(x) в точке х0. По аналогии с физикой производная функции f(x) в точке х0 характеризует скорость изменения данной функции в точке х0.
Определение. Производной функции f(x) в точке х0 называется число, к которому стремится разностное отношение ![]() при Δх, стремящемся к нулю. Производную функции f(x) в точке х0 обозначают f’(х0) (читают: эф штрих от х0), т. е.
при Δх, стремящемся к нулю. Производную функции f(x) в точке х0 обозначают f’(х0) (читают: эф штрих от х0), т. е. ![]()
Пример 3
Найдем производную функции f(х) = 3х2 + 2х в точке х0.
В соответствии с описанной схемой вычислим производную.
1) Найдем приращение функции: ![]()
![]()
2) Определим разностное отношение: ![]()
3) При Δх → 0 величина 3Δх → 0, слагаемые 6х0 и 2 постоянны (не зависят от Δх). Тогда отношение ![]() при Δх → 0. Поэтому f'(х) = 6х0 + 2 - производная функции f(х) = 3х2 + 2х в точке х0.
при Δх → 0. Поэтому f'(х) = 6х0 + 2 - производная функции f(х) = 3х2 + 2х в точке х0.
Пример 4
Найдем производную линейной функции f(x) = ax + b в точке x0 (где а и b постоянны).
Используя описанный алгоритм, вычислим производную.
1) Найдем приращение функции: ![]()
2) Определим разностное отношение: ![]()
3) Так как а - постоянная величина, то ![]() - постоянное число при любом значении Δх. Поэтому
- постоянное число при любом значении Δх. Поэтому ![]() при Δх → 0.
при Δх → 0.
Итак, f'(x0) = a - производная функции f(x) = ax + b в любой точке х0.
Функцию, имеющую производную в точке х0, называют дифференцируемой в этой точке. Пусть D - множество точек, в которых f(х) дифференцируема. Сопоставляя каждому х ∈ D число f'(х), получают новую функцию f'(x) с областью определения D. Эту функцию называют производной функции у = f(х) и обозначают f'(х) или y’(х). Нахождение производной данной функции f(х) называют дифференцированием функции f(х).
Обсудим, как связаны между собой непрерывность и дифференцируемость функции в точке. Справедливо утверждение: если функция у = f(х) дифференцируема в точке х0, то она и непрерывна в этой точке. Действительно, если функция у = f(х) дифференцируема в точке х0, то выполняется приближенное равенство Δf ≈ f'(х0)Δх. Если в этом равенстве устремить Δх к нулю, то и Δf будет стремиться к нулю. Тогда по определению функция у = f(х) непрерывна в точке х0.
Обратное утверждение: если функция у = f(х) непрерывна в точке х0, то она дифференцируема в ней - является неверным.
Пример 5
Рассмотрим функции f'(х) = |х| (рис. а) и ![]() (рис. б). Область определения этих функций D(f) = (-∞; +∞), т. е. функции непрерывны в каждой точке, в том числе в точке х0 = 0.
(рис. б). Область определения этих функций D(f) = (-∞; +∞), т. е. функции непрерывны в каждой точке, в том числе в точке х0 = 0.
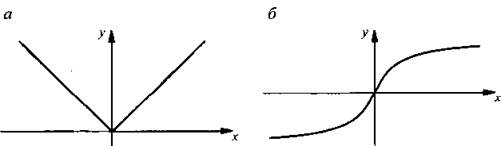
Если функция у = f(х) дифференцируема в точке х0, то к графику этой функции в точке А(х0; f(х0)) можно провести касательную. Причем угловой коэффициент к касательной равен f'(х0), т. е. к = f'(х0). В точке х0 = 0 к графику функции f(x) = |х| касательную провести нельзя, т. е. производная f'(x0) не существует. К графику функции ![]() в точке x0 = 0 построить можно, но она будет вертикальна, т. е. совпадает с осью 0у. Эта касательная образует с осью 0х прямой угол. Тангенс такого угла не существует. Поэтому не существуют также угловой коэффициент k и производная f'(х0).
в точке x0 = 0 построить можно, но она будет вертикальна, т. е. совпадает с осью 0у. Эта касательная образует с осью 0х прямой угол. Тангенс такого угла не существует. Поэтому не существуют также угловой коэффициент k и производная f'(х0).
IV. Контрольные вопросы
1. Понятие о касательной к графику функции.
2. Как найти угловой коэффициент касательной?
3. Вычисление мгновенной скорости движения.
4. Определение производной функции.
5. Какая функция называется дифференцируемой?
6. Что называется дифференцированием функции?
V. Задание на уроке
§ 27, № 1 (а, б); 3 (в); 4 (а, б); 5 (а); 9; 10 (а); 11 (в, г); 12 (а, б); 13 (в, г); 14 (а, б).
VI. Задание на дом
§ 27, № 1 (в, г); 3 (а); 4 (в, г); 5 (б); 10 (б); 11 (а, б); 12 (в, г); 13 (а, б); 14 (в, г).
VII. Подведение итогов урока