Алгебра и начала анализа 10 класс поурочные планы по учебнику Мордковича А. Г.
Вычисление производных - Производная - 2-е полугодие
Цель: изучить таблицу производных, правила дифференцирования.
Ход уроков
I. Сообщение темы и цели уроков
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (самостоятельная работа).
Вариант 1
1. Найдите производную функции f(x) = 4х - 5 в точке х0 = 3.
2. Напишите уравнение касательной, проведенной к графику функции f(х) = 3 - х2 в точке а = -1.
3. Определите мгновенную скорость точки, движущейся прямолинейно по закону S(t) = 2t1 + 5 в момент t0 = 4.
Вариант 2
1. Найдите производную функции f(х) = 3х + 4 в точке х0 = 2.
2. Напишите уравнение касательной, проведенной к графику функции f(х) = х2 + 2 в точке а = 1.
3. Определите мгновенную скорость точки, движущейся прямолинейно по закону S(t) = -4t2 + 3 в момент t0 = 3.
III. Изучение нового материала
На предыдущем занятии мы дали определение производной, объяснили ее физический и геометрический смысл. Теперь необходимо сделать следующий шаг. Для этого на сегодняшнем занятии рассмотрим формулы дифференцирования (таблицу производных) и правила дифференцирования.
1. Формулы дифференцирования (таблица производных)
Производные всех функций были получены с помощью определения производной.
Пример 1
Докажем, что f'(x) = -6х + 2, если f(х) = -3х2 + 2х.
1) Для произвольной точки х0 найдем приращение функции:
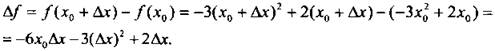
2) Определим разностное отношение: ![]() Найдем
Найдем ![]() так как функция
так как функция ![]() Поэтому f'(x) = -6x + 2.
Поэтому f'(x) = -6x + 2.
Пример 2
Найдем производную функции ![]()
1) Найдем приращение функции: ![]()
![]()
2) Преобразуем это выражение, умножив и разделив его на сопряженную величину: 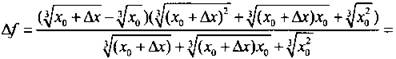
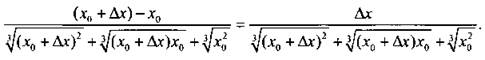
3) Найдем отношение приращения функции к приращению аргумента: 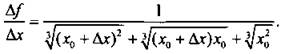
4) Вычислим предел этого отношения: 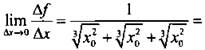
![]() Таким образом,
Таким образом, 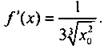
Пример 3
Найдем производную функции f(х) = sin х.
1) Найдем приращение функции: ![]()
![]() (была использована формула разности синусов).
(была использована формула разности синусов).
2) Составим разностное отношение: 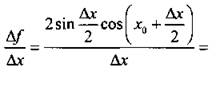
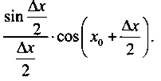
3) Найдем производную: 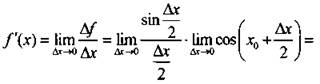
![]() Таким образом, было показано, что f'(x) = cos х.
Таким образом, было показано, что f'(x) = cos х.
Подобным образом можно составить таблицу производных основных функций, которая и далее будет пополняться (и ее, разумеется, надо помнить).
f(х) |
с |
х |
хn |
|
|
sin х |
cos x |
tg x |
ctg x |
f'(х) |
0 |
1 |
nxn-1 |
|
|
cos x |
-sin x |
|
|
f(х) |
arcsin x |
arccos x |
arctg x |
arcctg x |
f'(х) |
|
|
|
|
2. Правила дифференцирования
Рассмотрим правила, по которым можно дифференцировать сумму, произведение, частное функций.
Правило 1. Если функции f(х) и g(x) дифференцируемы в точке х, то и их сумма дифференцируема в точке х, причем производная суммы равна сумме производных: ![]()
Пример 4
Докажем правило 1.
1) Сумма функций f(х) и g(x) также является функцией h(x) = f(х) + g(x).
2) Найдем приращение функции h(x): ![]()
![]()
![]()
3) Определим отношение приращения функции Δh к приращению аргумента Δх: ![]()
4) Найдем предел этого отношения: ![]()
![]()
5) Таким образом, показано, что ![]()
Пример 5
Найдем производную функции ![]()
Используя правило 1, получим: ![]()
![]()
Правило 2. Если функция f(х) дифференцируема в точке х, то и функция kf(х) дифференцируема в точке х, причем ![]() Другими словами, постоянный множитель к можно вынести за знак производной.
Другими словами, постоянный множитель к можно вынести за знак производной.
Пример 6
Докажем правило 2.
Используем ту же схему доказательства, как и для правила 1.
1) Произведение kf(x) также является функцией h(x) = kf(х).
2) Найдем приращение функции h(х): ![]()
![]()
3) Определим отношение приращения функции Δh к приращению аргумента Δх: ![]()
4) Найдем предел этого отношения: ![]()
![]()
5) Показано, что ![]()
Пример 7
Найдем производную функции:
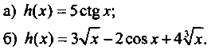
а) Используем правило 2 и получим: ![]()
![]()
б) Применим правила 1, 2 и получим: ![]()
![]()
![]()
Правило 3. Если функции f(x) и g(x) дифференцируемы в точке х, то и их произведение дифференцируемо в точке х, причем ![]() Другими словами, производная произведения двух функций равна сумме двух слагаемых: первое слагаемое есть произведение производной первой функции на вторую функцию, а второе слагаемое есть произведение первой функции на производную второй функции.
Другими словами, производная произведения двух функций равна сумме двух слагаемых: первое слагаемое есть произведение производной первой функции на вторую функцию, а второе слагаемое есть произведение первой функции на производную второй функции.
Это и следующие правила доказывать не будем. Данное доказательство аналогично доказательству правил 1 и 2, но технически сложнее.
Пример 8
Найдем производную функции g(x) = x3 tg х.
В соответствии с правилом 3 получим: ![]()
![]()
Заметим, что правило 2 является следствием правила 3. Действительно, если функция g(x) = k - постоянное число, то по правилу 3 получим: ![]() - правило 2.
- правило 2.
Правило 4. Если функции f(х) и g(x) дифференцируемы в точке х и в этой точке g(x) ≠ 0, то и функция f(x)/g(x) дифференцируема в точке х, причем 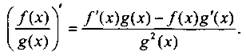
Пример 9
Найдем производную функции ![]()
По правилу 4 находим: 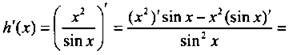
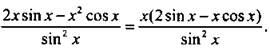
Отметим, что правило 4 может быть использовано для нахождения производных основных изучаемых функций.
Пример 10
Найдем производную функции h(x) = ctg х.
Запишем функцию в виде ![]() и используем правило 4. Получим:
и используем правило 4. Получим: 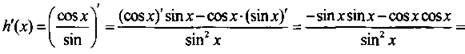
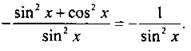 ---------
---------
Таким образом, получили, что ![]() (см. таблицу производных).
(см. таблицу производных).
3. Дифференцирование функции у = f(kx + m)
До сих пор рассматривались производные элементарных функций с аргументом х. Их нахождение труда не вызывает. Например, для функции у = х2 производная у' = 2х. Но для функции у = (2х + 3)2 уже возникают некоторые затруднения. Однако данное выражение можно возвести в квадрат: у - 4х2 + 12х + 9 и найти производную y’ = 4 · 2х + 12 = 4(2x + 3). Для функции у = (2x + 3)40 начинаются уже настоящие проблемы, так как возвести выражение в степень 40 нереально и применить предыдущий подход не удается. Поэтому для подобных ситуаций существует следующий алгоритм.
Правило 5. Производная функции f(kx + m) вычисляется по формуле ![]()
Пример 11
Найдем производную функции:
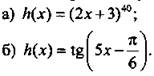
Применим правило 5.
а) В этом случае kх + m = 2х + 3, т. е. k = 2 и m = 3. Тогда получим: ![]()
б) Имеем: kх + m = 5х – π/6, т. е. k = 5 и m = -π/6. Находим производную: 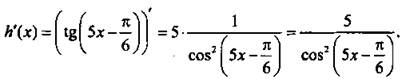
Теперь обобщим правило 5. Дело в том, что функция f(kx + m) - частный случай сложной функции, так как ее аргумент kх + m является, в свою очередь, линейной функцией переменной х.
Подавляющее большинство изучаемых функций являются сложными, например функции ![]()
![]() Разберемся с понятием сложной функции. Начнем с примера.
Разберемся с понятием сложной функции. Начнем с примера.
Пример 12
Вычислим по заданному значению х соответствующее значение z функции h, заданной формулой ![]() Для этого сначала вычислим по заданному значению х значение у = f(x) = 1 + x2. Потом по этому значению у найдем:
Для этого сначала вычислим по заданному значению х значение у = f(x) = 1 + x2. Потом по этому значению у найдем: ![]()
Таким образом, функция f(х) ставит в соответствие числу х число у, а функция g(y) - числу у число z. Совокупность этих операций называют сложной функцией h(х), составленной из функций g(y) и f(х), и записывают: h(x) = g(f(х)).
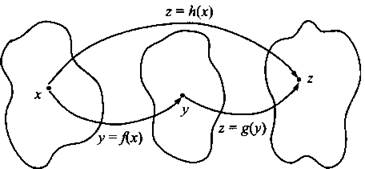
Чтобы вычислить значение сложной функции h(x) = g(f(x)) в произвольной точке x, сначала вычисляют значение у «внутренней» функции f в этой точке, а затем значение z функции g.
Теперь остановимся на производной сложной функции. Для ее вычисления существует правило.
Правило 6. Производная сложной функции h(x) = g(f(x)) вычисляется по формуле h'(x) = g’(f(x)) · f'(x).
Пример 13
Найдем производную функции:
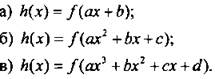
Используем правило 6 и получим:
![]() - сравните с правилом 5;
- сравните с правилом 5;
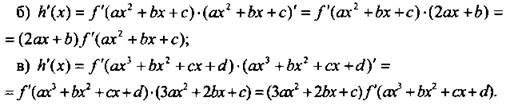
Пример 14
Найдем производную функции ![]()
Функция h(у) является сложной ![]() и
и ![]() Тогда
Тогда ![]() и
и ![]() Поэтому получим:
Поэтому получим: ![]()
Пример 15
Найдем производную функции ![]()
Функция h(x) является сложной h(x) = g(f(х)), где g(x) = cos у и у = f(x) – 5x3 + 2x. Тогда ![]() и g'(y) = (cos y)' = - sin у. Тогда получим:
и g'(y) = (cos y)' = - sin у. Тогда получим: ![]()
![]()
IV. Контрольные вопросы (фронтальный опрос)
1. Производные основных функций (таблица производных).
2. Правила дифференцирования.
3. Понятие сложной функции.
4. Производная сложной функции.
V. Задание на уроках
§ 28, № 5 (а, б); 8 (в, г); 9 (а, б); 13 (в, г); 15 (а); 17 (а, б); 18 (в, г); 23 (а, б); 25 (а); 27 (б); 28 (а); 30 (в, г); 43 (а, б); 44 (в, г).
VI. Задание на дом
§ 28, № 5 (в, г); 8 (а, б); 9 (в, г); 13 (а, б); 15 (в); 17 (в, г); 18 (а, б); 23 (в, г); 25 (б); 27 (а); 28 (б); 30 (а, б); 43 (в, г); 44 (а, б).
VII. Творческое задание
Найдите производную сложной функции:
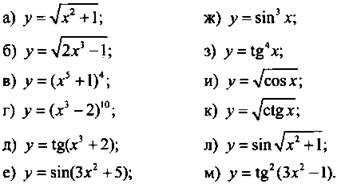
Ответы: ![]()
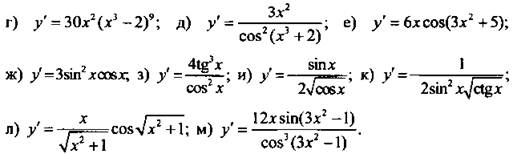
VIII. Подведение итогов уроков