Алгебра и начала анализа 10 класс поурочные планы по учебнику Мордковича А. Г.
Исследование функций (факультативное занятие) - Числовые функции - 1-е полугодие
Цель: отработать схему исследования функции, построения графика функции.
Ход уроков
I. Сообщение темы и цели уроков
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (письменный опрос).
Вариант 1
1. Дайте определения возрастающей функции и минимума функции.
2. Найдите промежутки возрастания и убывания, точки экстремума и экстремумы функции y = x2 - 3|x|, ее наименьшее и наибольшее значения на отрезке [-1; 4]. Постройте график функции.
Вариант 2
1. Дайте определения убывающей функции и максимума функции.
2. Найдите промежутки возрастания и убывания, точки экстремума и экстремумы функции y = 2|х| - х2, ее наименьшее и наибольшее значения на отрезке [-2; 3]. Постройте график функции.
III. Изучение нового материала
Построение графиков функций
В младших классах, пожалуй, единственным методом построения графиков функций был способ построения «по точкам». В случае хорошо изученных функций (линейной, квадратичной, дробно-линейной, степенной и т. д.) такой способ дает хорошие результаты. В случае незнакомой функции при использовании этого способа можно просмотреть какие-то принципиальные особенности поведения функции. Например, в физике очень распространены резонансные явления. Суть их состоит в том, что при плавном изменении какой-то физической величины вдруг возникает очень резкое ее увеличение или уменьшение.
Таким образом, для грамотного и обоснованного построения графика функции предварительно необходимо эту функцию исследовать. На примере покажем, какие этапы необходимо пройти при исследовании функции и построении ее графика.
Пример 1
Исследуем функцию ![]() и построим ее график.
и построим ее график.
1. Найдем область определения функции. Так как знаменатель х2 + 1 дроби не обращается в нуль, то D(y) - вся числовая прямая.
2. Определим особенности функции. Очевидно, что данная функция четная. Действительно, ![]() Поэтому исследуем и построим график функции при х ≥ 0. Затем эту часть графика отразим влево относительно оси ординат.
Поэтому исследуем и построим график функции при х ≥ 0. Затем эту часть графика отразим влево относительно оси ординат.
3. Найдем точки пересечения графика функции с осями координат. Чтобы найти точку пересечения с осью ординат, положим х = 0 и получим у = -1. Точка пересечения с осью ординат (0; -1). Чтобы найти точку пересечения с осью абсцисс, положим у = 0 и получим уравнение ![]() или 0 = x2 - 1, откуда х = 1. Точка пересечения с осью абсцисс (1; 0).
или 0 = x2 - 1, откуда х = 1. Точка пересечения с осью абсцисс (1; 0).
4. Выясним промежутки знакопостоянства функции, т. е. на каких промежутках функция принимает положительные значения, а на каких - отрицательные. Для нахождения промежутка отрицательности функции решим неравенство ![]() или x2 - 1 < 0, откуда 0 ≤ х < 1. Для нахождения промежутка положительности функции решим неравенство
или x2 - 1 < 0, откуда 0 ≤ х < 1. Для нахождения промежутка положительности функции решим неравенство ![]() или х2 - 1 > 0, откуда х > 1.
или х2 - 1 > 0, откуда х > 1.
5. Определим монотонность функции. Пусть х2 и х1 - две точки из промежутка [0; ∞), причем х2 > x1. Запишем функцию в виде ![]() Найдем разность
Найдем разность ![]()
![]() В этой дроби знаменатель всегда положительный. В числителе множитель x2 – x1 > 0 (так как x2 > x1), x2 + x1 > 0 (так как x1,2 > 0). Потому числитель дроби также положительный. Следовательно, дробь положительна, так как у(х2) - y(x1) > 0 или y(x2) > y(x1). Поэтому функция у(х) возрастает на промежутке [0; ∞). Учитывая четность функции y(x), на промежутке (-∞; 0] она убывает.
В этой дроби знаменатель всегда положительный. В числителе множитель x2 – x1 > 0 (так как x2 > x1), x2 + x1 > 0 (так как x1,2 > 0). Потому числитель дроби также положительный. Следовательно, дробь положительна, так как у(х2) - y(x1) > 0 или y(x2) > y(x1). Поэтому функция у(х) возрастает на промежутке [0; ∞). Учитывая четность функции y(x), на промежутке (-∞; 0] она убывает.
6. Найдем экстремумы функции. Так как только в точке х = 0 убывание функции сменяется возрастанием, то точка минимума xmin = 0 и минимум функции ymin = -1.
7. Выясним поведение функции при больших значениях х. Данная функция имеет вид: ![]() При неограниченном возрастании х знаменатель дроби х2 + 1 также неограниченно возрастает. Поэтому значения дроби
При неограниченном возрастании х знаменатель дроби х2 + 1 также неограниченно возрастает. Поэтому значения дроби ![]() приближаются к нулю, оставаясь положительными. Следовательно, значения функции у(х) неограниченно приближаются к 1, оставаясь меньше 1. Поэтому прямая у = 1 является горизонтальной асимптотой функции y(x).
приближаются к нулю, оставаясь положительными. Следовательно, значения функции у(х) неограниченно приближаются к 1, оставаясь меньше 1. Поэтому прямая у = 1 является горизонтальной асимптотой функции y(x).
8. Наименьшее значение функции yнаим = -1 достигается при х = 0, наибольшего значения нет.
9. Функция ограничена.
10. Функция непрерывная.
11. Выпуклость графика функции установить трудно (она меняется).
Исследованные свойства функции ![]() позволяют построить ее график. Сделаем сначала такое построение для промежутка х ∈ [0; ∞).
позволяют построить ее график. Сделаем сначала такое построение для промежутка х ∈ [0; ∞).
Построим точки пересечения с осями координат (0; -1), (1; 0). Учтем, что на промежутке [0; 1) значения у < 0, на промежутке (1; ∞) значения у > 0. Значения функции возрастают от y = -1 и стремятся к значению у = 1 при больших х. Проводим непрерывную кривую.
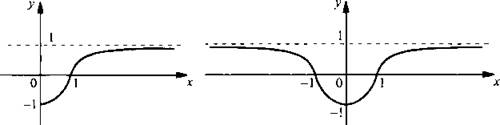
Учитывая четность данной функции y(x) отражаем кривую, построенную при х ≥ 0, влево симметрично относительно оси ординат. Получаем график функции y(x).
Схема исследования функции
На рассмотренном примере были фактически отработаны все этапы такого исследования. Они сводятся к следующему:
1. Найти области определения и значений функции y(x).
2. Выяснить особенности функции, облегчающие ее исследование и построение графика: а) четность или нечетность; б) периодичность.
3. Вычислить координаты точек пересечения графика функции с осями координат.
4. Найти промежутки знакопостоянства функции.
5. Определить промежутки возрастания и промежутки убывания функции.
6. Найти точки экстремума, определить вид экстремума (максимум или минимум), вычислить экстремум функции.
7. Исследовать поведение функции в окрестности точек разрыва (как правило, возникают вертикальные асимптоты) и при больших по модулю значениях аргумента (могут возникать горизонтальные или наклонные асимптоты).
8. Найти наименьшее и наибольшее значения функции.
Заметим, что этот план носит ориентировочный характер. Практически любой пункт плана может вызвать технические трудности, например даже в пункте 1 при нахождении области определения и значений данной функции f(х). Предположим, что функция f(х) рациональная, т. е. имеет вид: ![]() (где h(x), g(x) – некоторые многочлены). Тогда область определения функции f(х) задается условием g(x) ≠ 0. Поэтому необходимо найти корни многочлена g(x). Если этот многочлен имеет степень выше второй и иррациональные корни, то такая задача практически нерешаема. Нахождение области значений функции f(х) является еще более тяжелой задачей. Для этого необходимо найти промежутки монотонности функции f(х), ее экстремумы, исследовать поведение функции f(х) при больших значениях |х|. Эти процедуры можно выполнить только с помощью теории предела функции, которая изучается в школе в очень урезанном объеме (см. главу 5).
(где h(x), g(x) – некоторые многочлены). Тогда область определения функции f(х) задается условием g(x) ≠ 0. Поэтому необходимо найти корни многочлена g(x). Если этот многочлен имеет степень выше второй и иррациональные корни, то такая задача практически нерешаема. Нахождение области значений функции f(х) является еще более тяжелой задачей. Для этого необходимо найти промежутки монотонности функции f(х), ее экстремумы, исследовать поведение функции f(х) при больших значениях |х|. Эти процедуры можно выполнить только с помощью теории предела функции, которая изучается в школе в очень урезанном объеме (см. главу 5).
Остановимся на понятии асимптот графика функции f(x). Асимптоты разделяются на два вида - вертикальные и наклонные (в частности, горизонтальные). Строгое определение асимптот может быть дано только с помощью теории предела функции. Поэтому ограничимся только понятием асимптот.
Вертикальная прямая х = а называется вертикальной асимптотой функции f(х), если при приближении значений х к величине а значения функции f(x) неограниченно возрастают или убывают, т. е. при х → а f(х) → ±∞.
Пример 2
Рассмотрим функцию ![]() и построим ее график.
и построим ее график.
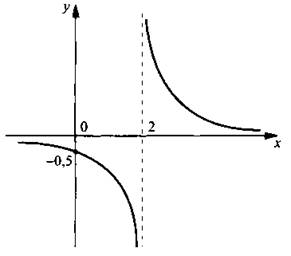
Г рафик данной функции получается из графика функции у = 1/x его смещением на 2 единицы вправо. Видно, что при х → 2 (при этом х < 2) знаменатель х - 2 отрицательный и х - 2 → 0. Поэтому значения функции ![]() неограниченно убывают, т. е. у → -∞. При х → 2 (при этом х > 2) знаменатель х - 2 положительный и х - 2 → 0. Поэтому значения функции
неограниченно убывают, т. е. у → -∞. При х → 2 (при этом х > 2) знаменатель х - 2 положительный и х - 2 → 0. Поэтому значения функции ![]() неограниченно возрастают, т. е. у → ∞. Следовательно, вертикальная прямая х = 2 является вертикальной асимптотой данной функции
неограниченно возрастают, т. е. у → ∞. Следовательно, вертикальная прямая х = 2 является вертикальной асимптотой данной функции ![]() .
.
Из примера видно, что часто в случае рациональных функций вертикальными асимптотами являются те значения х, при которых знаменатель дроби обращается в нуль. Однако не всегда в случае рациональных функций возникают вертикальные асимптоты (даже если знаменатель дроби обращается в нуль).
Пример 3
Построим график функции ![]()
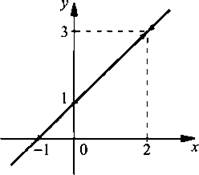
Разложим числитель данной дроби на множители и сократим ее. Получаем: ![]() (при этом х ≠ 2). Видно, что при х → 2 значения функции у → 3. Поэтому данная функция вертикальной асимптоты не имеет. Существует только значение х = 2, при котором функция не определена.
(при этом х ≠ 2). Видно, что при х → 2 значения функции у → 3. Поэтому данная функция вертикальной асимптоты не имеет. Существует только значение х = 2, при котором функция не определена.
Обратимся теперь к понятию наклонной асимптоты. Прямая у = kx + b называется наклонной асимптотой функции f(х), если при неограниченном возрастании или убывании х значения функции f(х) стремятся к значениям линейной функции y(x), т. е. при х → ±∞ f(х) → у(х).
Пример 4
Построим график функции ![]()
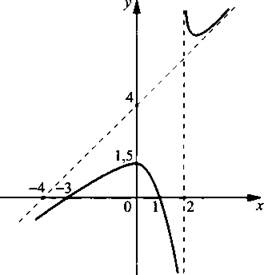
Найдем точки пересечения графика функции с осями координат. При x = 0 находим: ![]() - точка пересечения с осью ординат. При у = 0 получаем уравнение
- точка пересечения с осью ординат. При у = 0 получаем уравнение ![]() или 0 = х2 + 2х - 3, корни которого x1 = -3 и x2 = 1 - точки пересечения с осью абсцисс.
или 0 = х2 + 2х - 3, корни которого x1 = -3 и x2 = 1 - точки пересечения с осью абсцисс.
Очевидно, что прямая х = 2 - вертикальная асимптота. При х → 2 числитель дроби х + 2х – 3 → 22 + 2 · 2 - 3 = 5. При х < 2 знаменатель дроби х - 2 отрицательный и х - 2 → 0. Поэтому значения функции у → -∞. При х > 2 знаменатель дроби х - 2 положительный и х - 2 → 0. Поэтому значения функции у → ∞.
Разделим числитель дроби х2 + 2х - 3 на ее знаменатель х - 2 столбиком и выделим целую часть. Тогда функция у(х) имеет вид ![]() Очевидно, при x → ∞ дробь
Очевидно, при x → ∞ дробь ![]() и значения функции y(х) стремятся к значениям линейной функции у = х + 4. Поэтому линейная функция у = х + 4 является наклонной асимптотой для данной функции y(x).
и значения функции y(х) стремятся к значениям линейной функции у = х + 4. Поэтому линейная функция у = х + 4 является наклонной асимптотой для данной функции y(x).
Учитывая точки пересечения графика функции с осями координат, наличие вертикальной и наклонной асимптот, строим график данной функции. Очевидно, что график функции не пересекает асимптоты. На графике видно, что функция имеет максимум и минимум (найти их координаты можно только с помощью производной).
Частным случаем наклонной асимптоты является горизонтальная асимптота (при k = 0). Горизонтальная прямая у = b называется горизонтальной асимптотой функции f(х), если при неограниченном возрастании или убывании х значения функции f(x) стремятся к величине b, т. е. при х → ±∞ f(x) → b.
Пример 5
Построим график функции ![]()
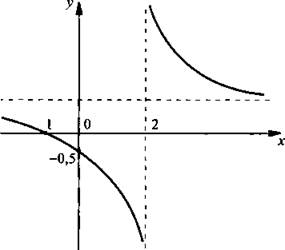
Найдем точки пересечения графика функции с осями координат. При х = 0 находим: у = -0,5 - точка пересечения с осью ординат. При у = 0 получаем уравнение ![]() или 0 = x + 1, корень которого х = -1 - точка пересечения с осью абсцисс.
или 0 = x + 1, корень которого х = -1 - точка пересечения с осью абсцисс.
Очевидно, что прямая x = 2 - вертикальная асимптота. При х → 2 числитель дроби x + 1 → 3. При x < 2 знаменатель дроби x - 2 отрицательный и x - 2 → 0. Поэтому значения функции у → -∞. При x > 2 знаменатель дроби x - 2 положительный и x - 2 → 0. Поэтому значения функции у → ∞.
Разделим числитель дроби x + 1 на ее знаменатель x - 2 столбиком и выделим целую часть. Тогда функция y(x) имеет вид: ![]()
Очевидно, при х → ∞ дробь ![]() и значения функции у(х) стремятся к 1. Поэтому прямая у = 1 является горизонтальной асимптотой для графика данной функции
и значения функции у(х) стремятся к 1. Поэтому прямая у = 1 является горизонтальной асимптотой для графика данной функции ![]()
Учитывая проведенное исследование данной функции, строим ее график. Очевидно, что такой график получается смещением графика функции у = 3/x на 2 единицы вправо и на 1 единицу вверх.
Чтение графиков функций
Практически во всех исследованиях результаты представляются в виде графиков. Поэтому необходимо уметь их читать, т. е. понимать и представлять свойства функций, которые им соответствуют.
Пример 6
На рис. а представлена зависимость х(t) для точки, двигающейся из пункта А в пункт В (где х - координата точки, начало отсчета совмещено с пунктом А).
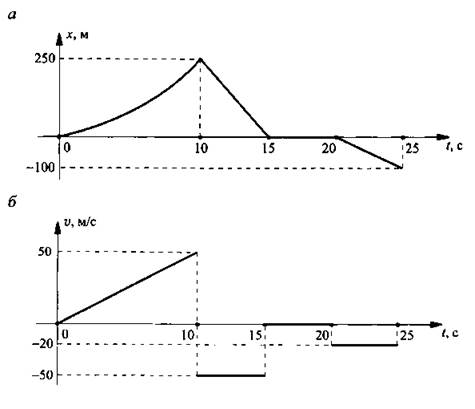
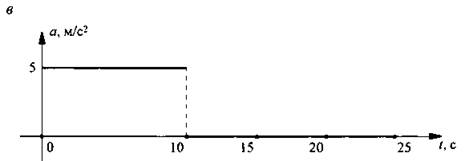
Опишем происходящее движение, которое дополнительно будем иллюстрировать графиками б: зависимостью скорости от времени v(t) и в: зависимостью ускорения от времени a(t). При этом координата (перемещение) х измеряется в м, скорость v - в м/с, ускорение a - в м/с2, время t – в с.
На промежутке 0 ÷ 10 с перемещение х меняется по квадратичному закону, т. е. движение является равноускоренным. Поэтому скорость v меняется по линейному закону и ускорение а постоянно. При этом точка движется по направлению от А к В, так как перемещение х имеет положительный знак.
При t = 10 с точка изменяет направление движения на противоположное и начинает двигаться к пункту А. При этом координата х меняется по линейному закону, т. е. движение является равномерным со скоростью v = -50 м/с. Отрицательный знак скорости при t = 10 ÷ 15 с указывает на движение в направлении к пункту А. Очевидно, что ускорение a = 0.
В течение времени t = 15 ÷ 20 с координата х не меняется и х = 0. Это означает, что точка находится в состоянии покоя в пункте А. Разумеется скорость v = 0 и ускорение a = 0.
На промежутке t = 20 ÷ 25 с координата х меняется по линейному закону, т. е. движение является равномерным со скоростью v = -20 м/с. Отрицательные знаки перемещения х и скорости v указывают на удаление точки от пунктов А и В. Разумеется, ускорение a = 0.
IV. Контрольные вопросы
1. Приведите схему исследования функции.
2. Дайте определение вертикальной асимптоты графика функции.
3. Приведите определение наклонной асимптоты графика функции.
4. Дайте определение горизонтальной асимптоты графика.
V. Творческое задание
Проведите исследование функции и постройте ее график:
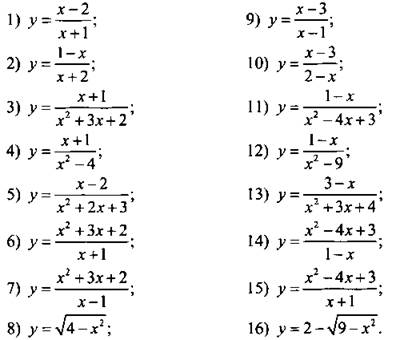
VI. Подведение итогов уроков