проверить знания и умения учащихся нахождения первообразных функции в случаях, непосредственно сводящихся к применению таблицы и трём правилам нахождения первообразных; рассмотреть более сложные упражнения по этой теме - ТРИ ПРАВИЛА НАХОЖДЕНИЯ ПЕРВООБРАЗНЫХ - ПЕРВООБРАЗНАЯ - 1-е полугодие

Цели: проверить знания и умения учащихся нахождения первообразных функции в случаях, непосредственно сводящихся к применению таблицы и трём правилам нахождения первообразных; рассмотреть более сложные упражнения по этой теме.

Ход урока

I. Устные упражнения

Найдите одну из первообразных функции f:

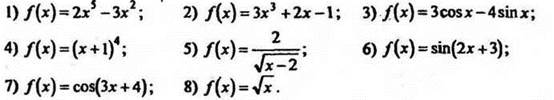
Ответы:

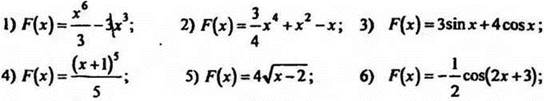
(внести в таблицу первообразных, х(0;∞)).

II. Решение упражнений

№ 352 (a).

Решение

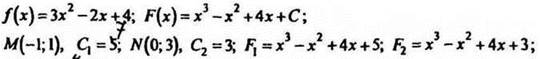
F1 – F2 =2. График F1 расположен выше.

№ 352 (г).

Решение

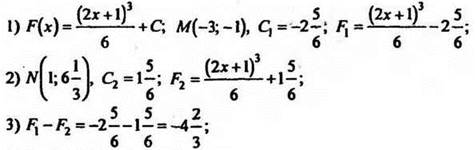
4) график F2 расположен выше.

III. Самостоятельная работа

К каждой задаче даны четыре ответа, только один из которых верен. Учащийся должен в специальном бланке поставить номер своего варианта и зачеркнуть номер выбранного им ответа по каждому заданию.

Учитель изготовляет шаблон с отверстиями (отверстия заштрихованы), накладывая который на бланки учащихся можно установить правильность решения каждой из четырёх задач. Верные ответы занумерованы во всех вариантах самостоятельных работ так, что они могут быть проверены одним и тем же шаблоном. Шаблон накладывается на бланк так, чтобы надпись соответствующего варианта была вверху. При необходимости можно составить и этим же способом при помощи шаблона проверить 8 вариантов. Для этого используется обратная сторона шаблона и соответствующим образом кодируются верше ответы. Работы могут быть проверены на этом же уроке.

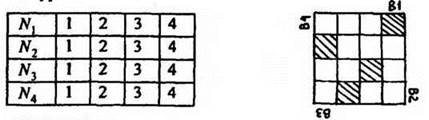
Вариант I

1. При каком значении k функция является первообразной функции Ответ: 1) -5; 2) 5; 3) -6; 4) 6.

2. Найдите первообразную функции 2х + 1.

Ответ:

3. Найдите первообразную функции

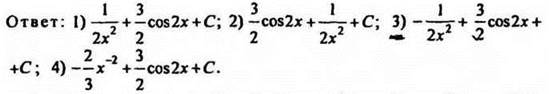
4. Найдите первообразную функции 2cosx, если график этой первообразной проходит через точку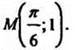

Ответ:

Вариант II

1. При каких значениях k функция является первообразной функции 8х + ? Ответ: 1) 4; 2) -4; 3) 1/8; 4) 3.

2. Найдите первообразную функции

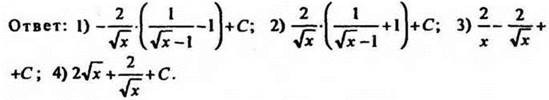
3. Найдите первообразную функции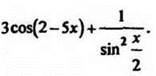

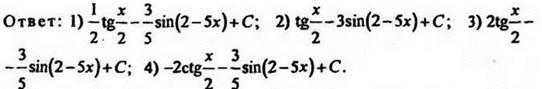
4. Найдите первообразную функции 2sinx, если график этой первообразной проходит через точку

Ответ:

Вариант III

1. При каком значении к функция является первообразной функции 5cos + 2х.

Ответ:

2. Найдите первообразную функции

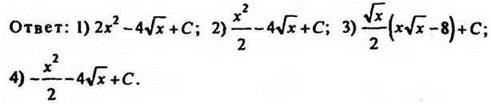
3. Найдите первообразную функции

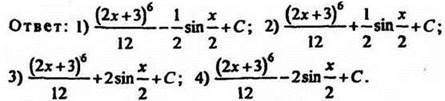
4. Найдите первообразную функции если график этой первообразной проходит через точку

Ответ:

Вариант IV (для сильных учащихся)

1. При каких значениях k функции kcosx + x - 4 является первообразной функции 3sinх + 1? Ответ: 1) не существует, 2) 3; 3) -3; 4) 0.

2. Найдите первообразную функции

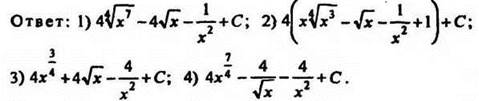
3. Найдите первообразную функции

4. Найдите первообразную функции 2sin2х, если график этой первообразной проходит через точку (0;1).

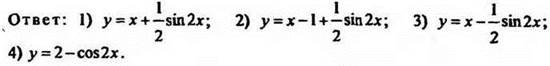
IV. Итоги урока

V. Домашнее задание: п. 26-28; № 352(б; в); подготовиться к контрольной работе.

10. Докажите, что функция F есть первообразная для функции f на указанном промежутке:

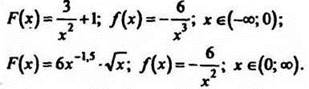
20. Найдите общий вид первообразной на промежутке (-0,5;∞).

3°. Для функции f(x) = 2х + 4 найдите первообразную F(х), график которой проходит через точку В(-1;1). Начертите график функции F(x).